
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
§5. Функціональні ряди.
Функціональний
ряд – це ряд, членами якого є функції
![]() ,
визначені в деякій області
,
визначені в деякій області
![]() .
Отже функціональний ряд має вигляд
.
Отже функціональний ряд має вигляд
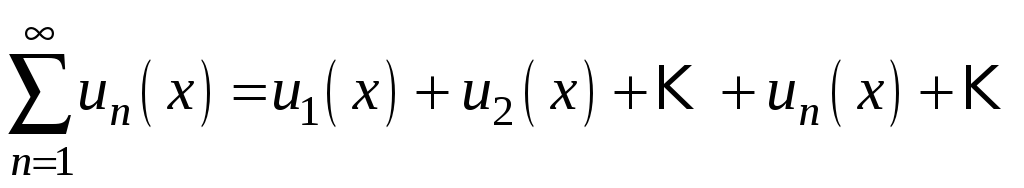
![]()
У
будь-який точці
![]() функціональний ряд перетворюється на
числовий:
функціональний ряд перетворюється на
числовий:
![]() ,
який може виявитися збіжним або розбіжним.
Якщо числовий ряд
,
який може виявитися збіжним або розбіжним.
Якщо числовий ряд
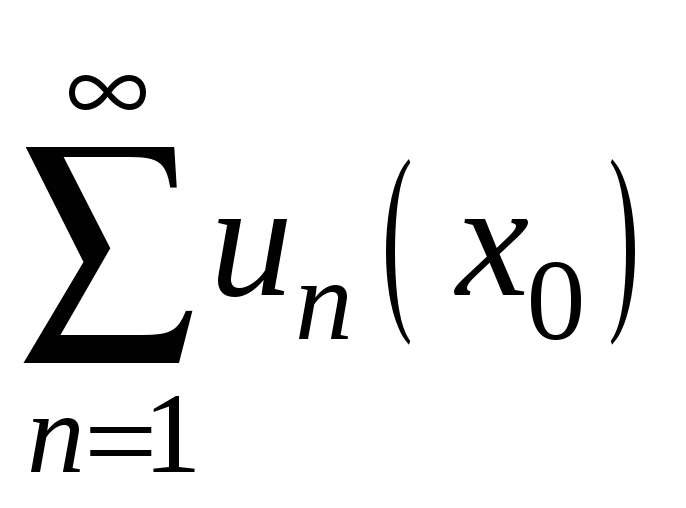 збігається (розбігається), то кажуть,
що функціональний ряд
збігається (розбігається), то кажуть,
що функціональний ряд
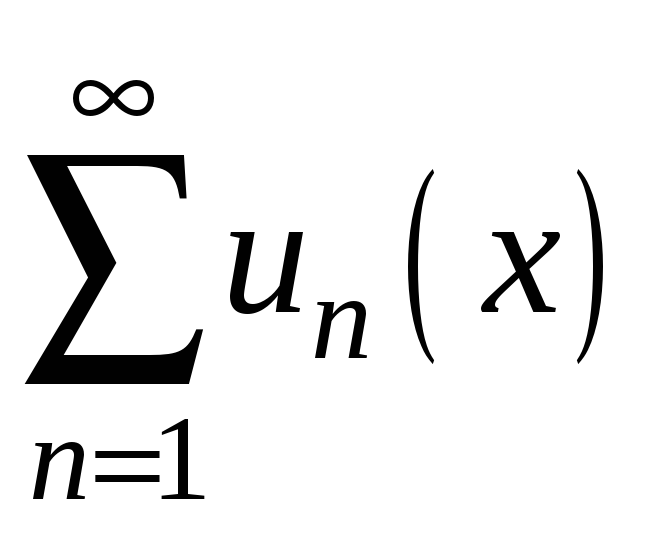 збігається (розбігається) в точці
збігається (розбігається) в точці
![]() .
Сукупність всіх таких точок, в яких
збігається ряд (3.7), називається його
областю збіжності.
.
Сукупність всіх таких точок, в яких
збігається ряд (3.7), називається його
областю збіжності.
Часткова
сума ряду (3.7)
![]() - функція змінної
- функція змінної
![]() .
Для будь-якого числа
.
Для будь-якого числа
![]() ,
що належить області збіжності, виконано
,
що належить області збіжності, виконано
![]() .
Функція
.
Функція
![]() називається сумою функціонального
ряду. Тобто
називається сумою функціонального
ряду. Тобто
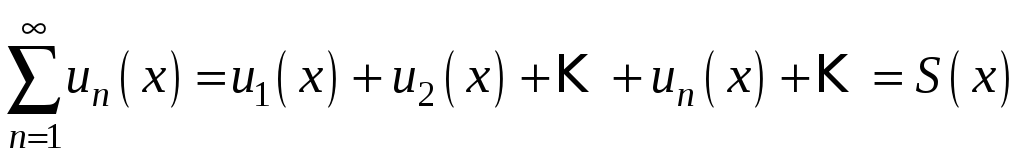 .
.
Залишок
ряду
![]() - це також функція визначена в області
збіжності цього ряду. Як бачимо,
- це також функція визначена в області
збіжності цього ряду. Як бачимо,
![]() .
.
Ряд
(3.7) називається мажоровним на відрізку
![]() ,
якщо існує такий збіжний ряд з додатними
членами
,
якщо існує такий збіжний ряд з додатними
членами
![]() ,
що
,
що
![]() ,
,
![]() ,
,
![]() .
При цьому
.
При цьому
![]() називається мажорантою або мажоруючим
рядом. Наприклад, ряд
називається мажорантою або мажоруючим
рядом. Наприклад, ряд
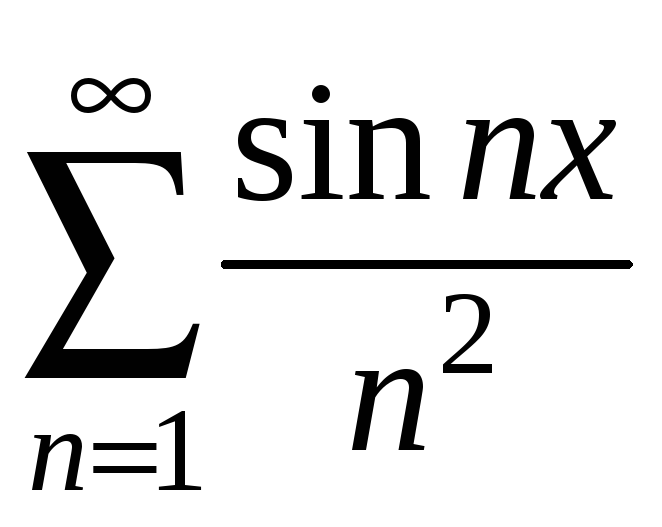 має мажоранту
має мажоранту
![]() ,
оскільки
,
оскільки
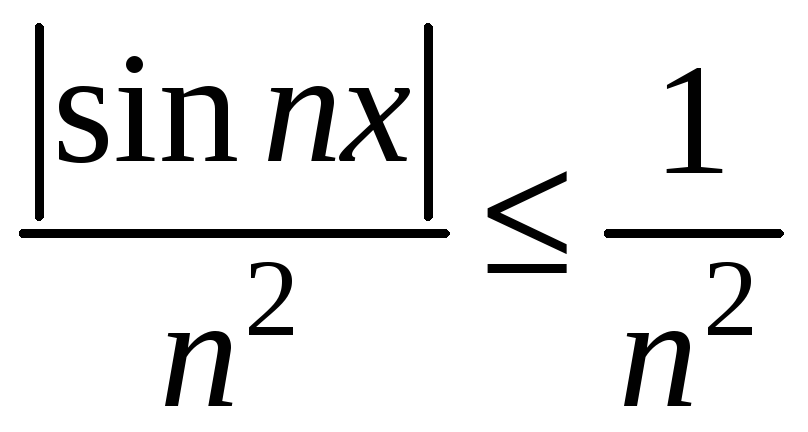 ,
,
![]() ,
,
![]() ,
і ряд
,
і ряд
![]() збігається. Безпосередньо з самого
означення випливає, що мажоровний на
відрізку
збігається. Безпосередньо з самого
означення випливає, що мажоровний на
відрізку
![]() ряд абсолютно збігається в усіх точках
цього відрізка.
ряд абсолютно збігається в усіх точках
цього відрізка.
Сформулюємо без доведення основні властивості мажоровних рядів.
Теорема
3.16 Нехай
функціональний
ряд
(3.7) мажоровний на відрізку
![]() .
Тоді для будь-якого додатного числа
.
Тоді для будь-якого додатного числа
![]() знайдеться такий номер
знайдеться такий номер
![]() ,
що для всіх
,
що для всіх
![]() нерівність
нерівність
![]() (
(![]() - сума залишку ряду (3.7) після
- сума залишку ряду (3.7) після
![]() - го члена) виконується одразу для всіх
- го члена) виконується одразу для всіх
![]() .
.
Теорема
3.17 Якщо
всі члени мажоровного на відрізку
![]() ряду неперервні, то його сума
ряду неперервні, то його сума
![]() також неперервна на
також неперервна на
![]() .
.
Теорема
3.18 Нехай
ряд (3.7) з неперервних функцій є мажоровним
на
![]() ,
,
![]() - його сума. Тоді ряд можна почленно
інтегрувати по проміжку
- його сума. Тоді ряд можна почленно
інтегрувати по проміжку
![]() і виконана рівність:
і виконана рівність:
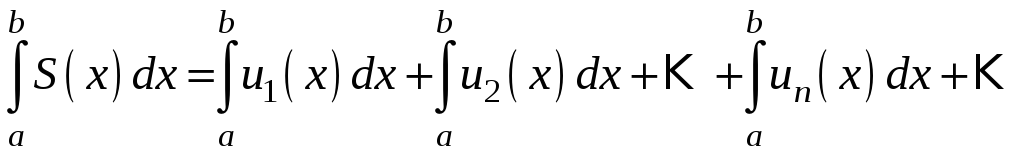 .
.
Теорема
3.19 Нехай
ряд, складений із функцій
![]() ,
що мають неперервні похідні
,
що мають неперервні похідні
![]() ,
збігається на відрізку
,
збігається на відрізку
![]() .
Якщо ряд
.
Якщо ряд
![]() ,
складений з похідних, мажоровний на
,
складений з похідних, мажоровний на
![]() ,
то справедлива рівність:
,
то справедлива рівність:
![]() .
.
§6. Степеневий ряд.
Степеневим рядом називається функціональний ряд виду
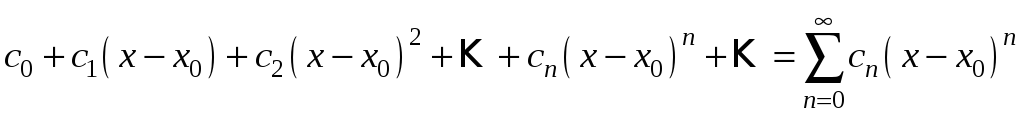 ,
,
де
![]() - деякі числа. Числа
- деякі числа. Числа
![]() називають коефіцієнтами степеневого
ряду. Якщо
називають коефіцієнтами степеневого
ряду. Якщо
![]() ,
то степеневий ряд має вигляд:
,
то степеневий ряд має вигляд:
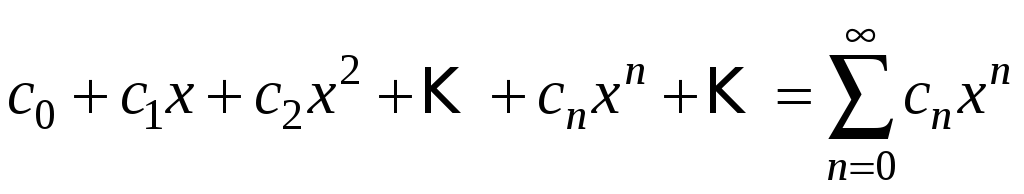 .
.
Степеневий
ряд
 за допомогою заміни
за допомогою заміни
![]() зводиться до ряду
зводиться до ряду
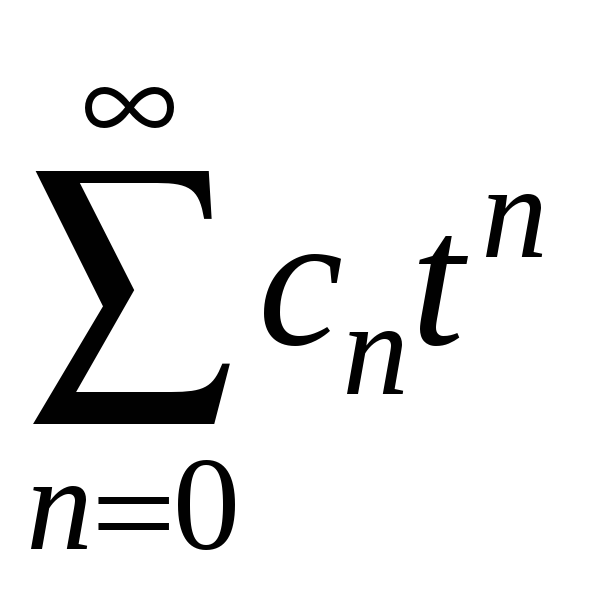 ,
тому надалі кажучи про степеневий ряд,
будемо мати на увазі тільки ряди виду
,
тому надалі кажучи про степеневий ряд,
будемо мати на увазі тільки ряди виду
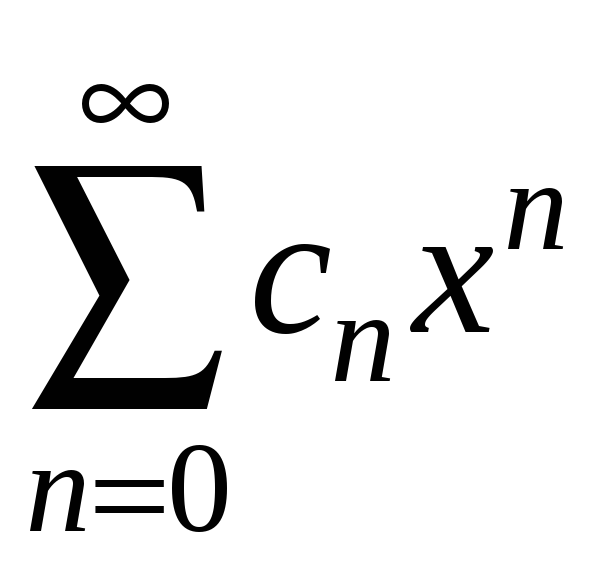 .
.
Теорема 3.20 (теорема Абеля).
1. Якщо
степеневий ряд збігається у точці
![]() ,
то він абсолютно збігається у будь-якій
точці
,
то він абсолютно збігається у будь-якій
точці
![]() ,
для якої виконано:
,
для якої виконано:
![]() .
.
2. Якщо
степеневий ряд розбігається у точці
![]() ,
то він розбігається при будь-якому
,
то він розбігається при будь-якому
![]() ,
для якого:
,
для якого:
![]() .
.
Доведення.
Якщо
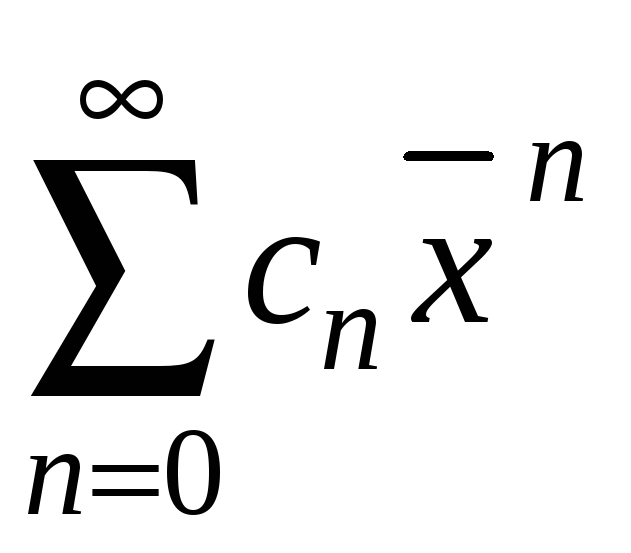 збігається, то його загальний член
збігається, то його загальний член
![]() прямує до 0, коли
прямує до 0, коли
![]() .
Тоді існує таке число
.
Тоді існує таке число
![]() ,
що
,
що
![]() .
Нехай
.
Нехай
![]() - будь-яке число, для якого виконано:
- будь-яке число, для якого виконано:
![]() ,
тобто
,
тобто
![]() .
Розглянемо ряд
.
Розглянемо ряд
 .
Для його членів маємо:
.
Для його членів маємо:
 .
Таким чином, модулі членів цього ряду
не перевищують членів збіжного
геометричного ряду
.
Таким чином, модулі членів цього ряду
не перевищують членів збіжного
геометричного ряду
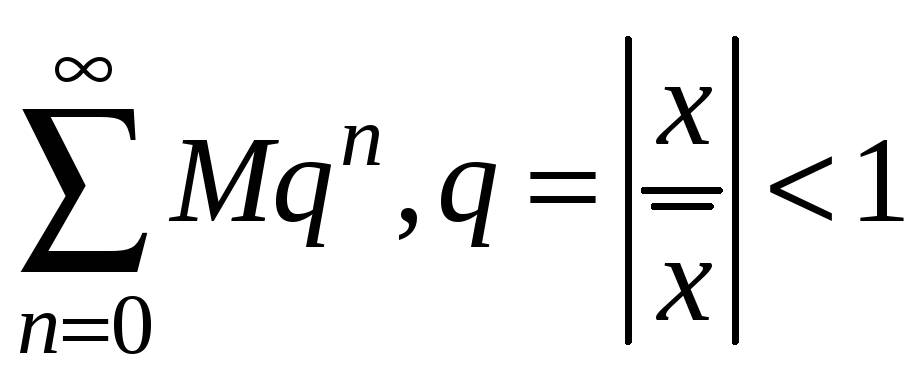 .
Тоді ряд
.
Тоді ряд
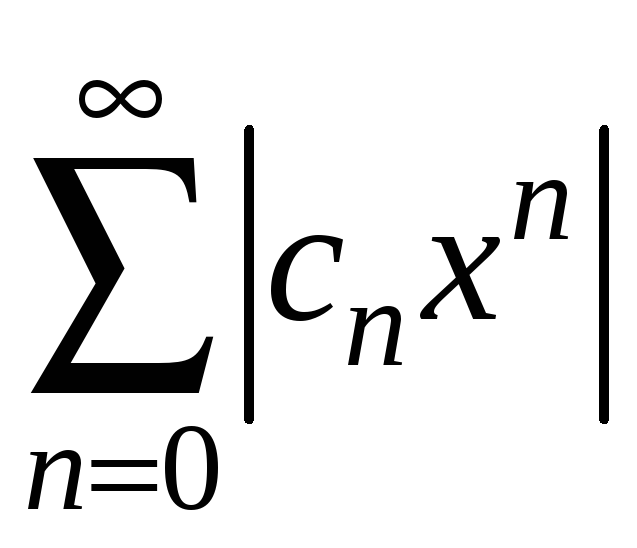 збігається. Отже ряд
збігається. Отже ряд
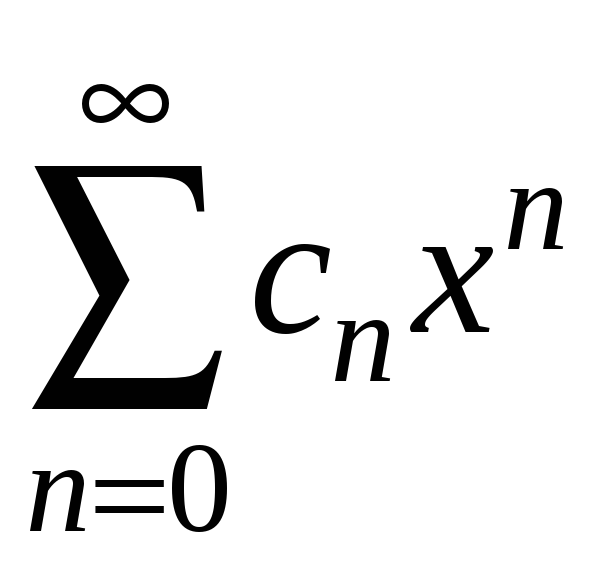 збігається абсолютно.
збігається абсолютно.
2. Нехай
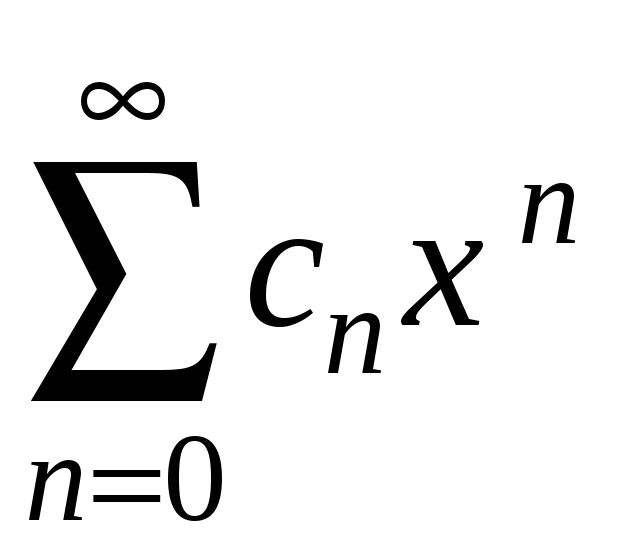 розбігається в точці
розбігається в точці
![]() .
Якби він міг збігатися в якій-небудь
точці
.
Якби він міг збігатися в якій-небудь
точці
![]() ,
,
![]() ,
то (за доведеним у першому пункті) він
збігався б в усіх точках, в яких
,
то (за доведеним у першому пункті) він
збігався б в усіх точках, в яких
![]() .
Таким чином, збігався б і ряд
.
Таким чином, збігався б і ряд
 .
Отримане протиріччя доводить другий
пункт теореми.
.
Отримане протиріччя доводить другий
пункт теореми.
Розглянемо
питання про те , як знайти область
збіжності степеневого ряду. З’ясуємо
спочатку , при яких значеннях
![]() степеневий ряд є абсолютно збіжним.
Дослідимо ряд з модулів
степеневий ряд є абсолютно збіжним.
Дослідимо ряд з модулів
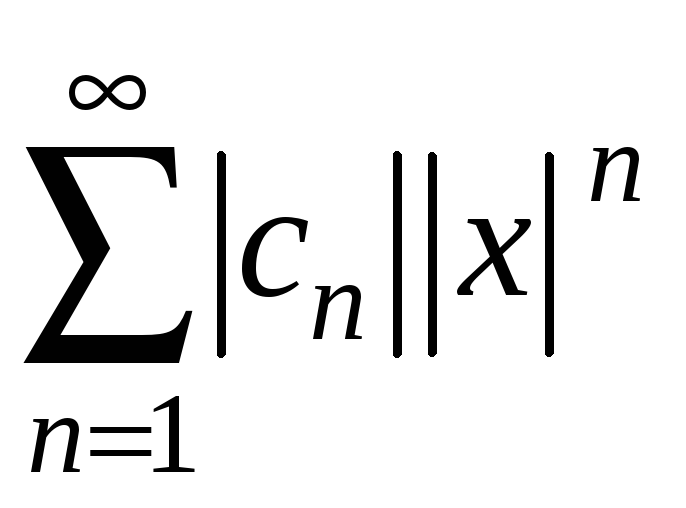 за ознакою Даламбера:
за ознакою Даламбера:
![]() ,
,
![]() ,
,
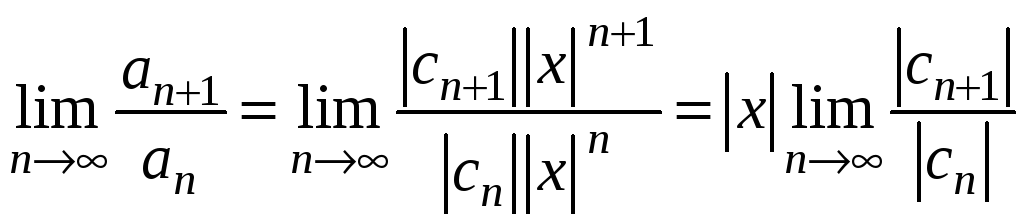 .
Ряд з модулів збігається при таких
значеннях
.
Ряд з модулів збігається при таких
значеннях
![]() ,
що
,
що
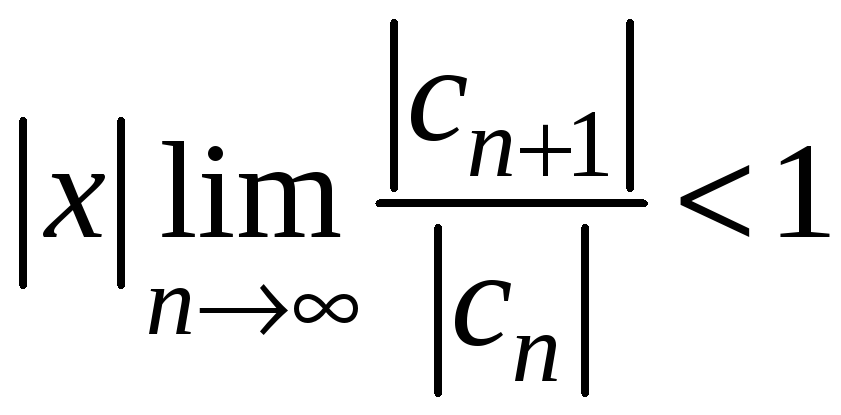 ,
тобто при
,
тобто при
 .
Введемо позначення
.
Введемо позначення
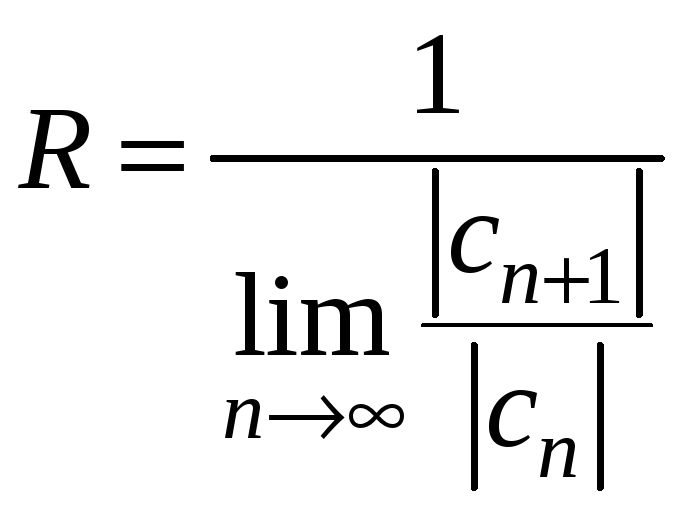 .
Отже в інтервалі
.
Отже в інтервалі
![]() або
або
![]() степеневий ряд збігається абсолютно.
Якщо
степеневий ряд збігається абсолютно.
Якщо
![]() ,
то для ряду з модулів маємо
,
то для ряду з модулів маємо
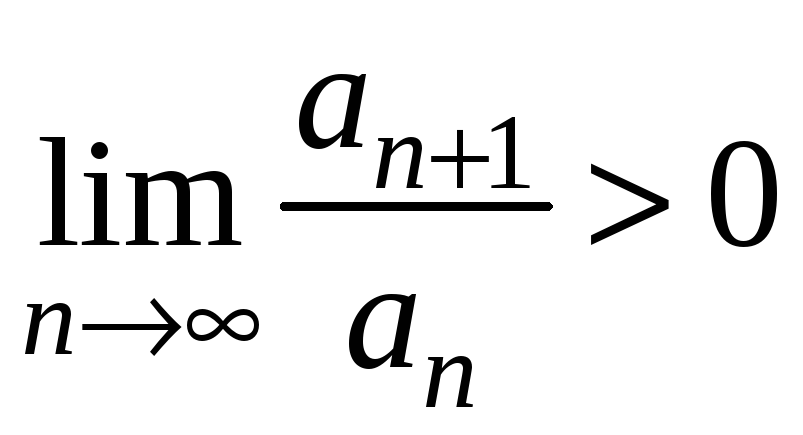 ,
тобто ряд
,
тобто ряд
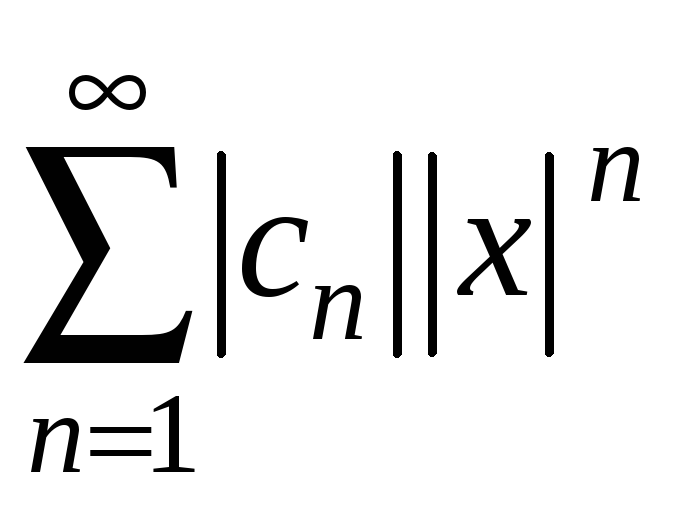 розбігається на підставі необхідної
умови збіжності (
розбігається на підставі необхідної
умови збіжності (![]() ).
Тоді загальний член степеневого ряду
також не прямує до
).
Тоді загальний член степеневого ряду
також не прямує до
![]() при
при
![]() .
Таким чином, степеневий ряд збігається
в інтервалі
.
Таким чином, степеневий ряд збігається
в інтервалі
![]() і розбігається при
і розбігається при
![]() .
Інтервал
.
Інтервал
![]() називають інтервалом збіжності
степеневого ряду, число
називають інтервалом збіжності
степеневого ряду, число
![]() -
радіусом збіжності. Для того, щоб
дізнатись, чи приєднувати до області
збіжності точки
-
радіусом збіжності. Для того, щоб
дізнатись, чи приєднувати до області
збіжності точки
![]() ,
їх слід підставити в ряд
,
їх слід підставити в ряд
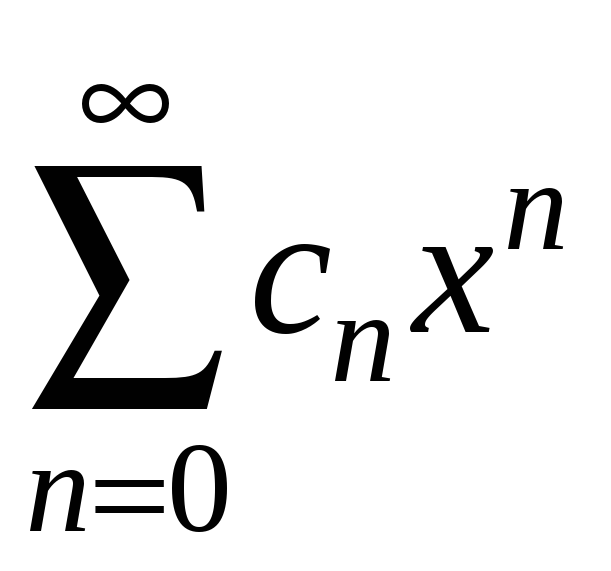 і дослідити отримані числові ряди.
і дослідити отримані числові ряди.
Приклад.
Знайти
область збіжності степеневого ряду
 .
.
Розв’язання.
Дослідимо
ряд з модулів
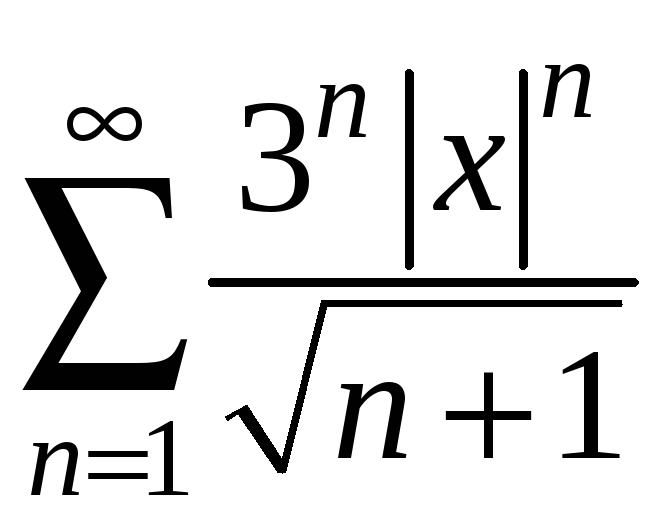 .
Застосуємо ознаку Даламбера:
.
Застосуємо ознаку Даламбера: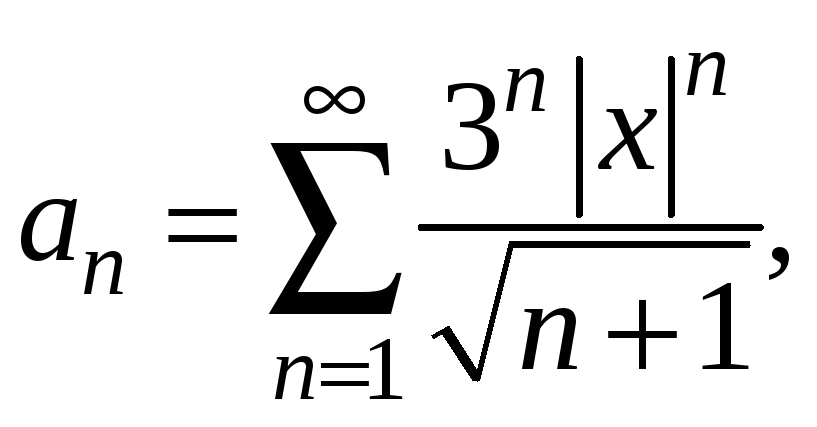
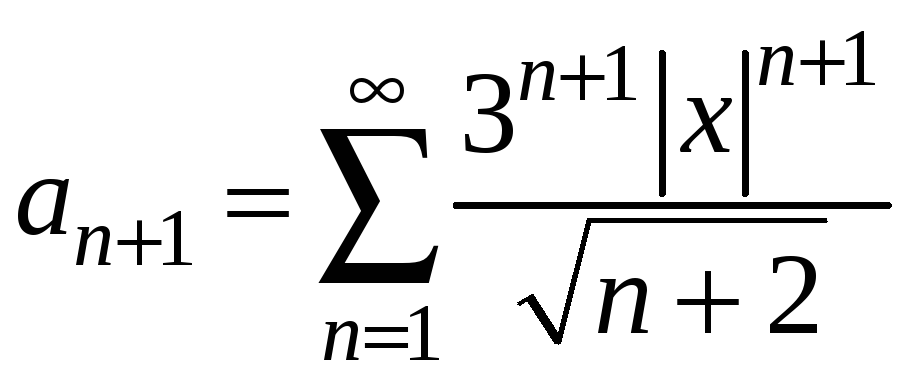 ,
,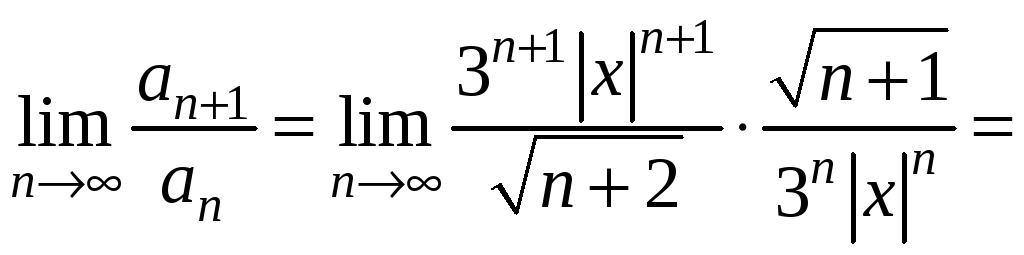
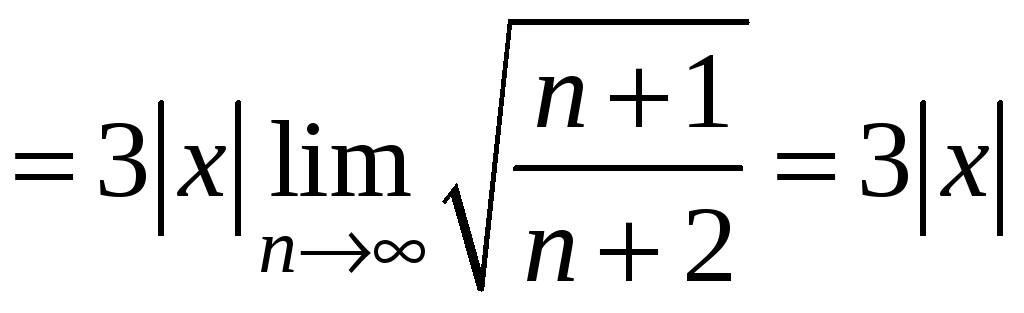 .
.
Інтервал
збіжності степеневого ряду:
![]() .
Якщо
.
Якщо
![]() ,
то ряд розбігається. Залишилось дослідити
ряд
,
то ряд розбігається. Залишилось дослідити
ряд
 при
при
![]() .
.
При
![]() одержимо числовий ряд
одержимо числовий ряд
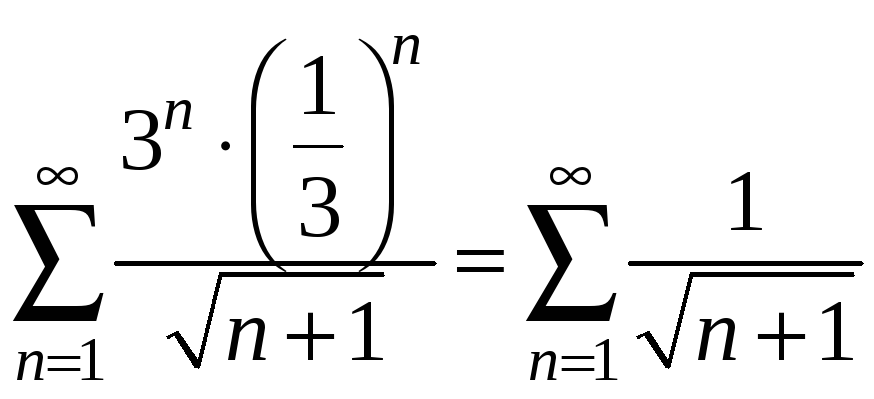 ,
який розбігається за ознакою порівняння
(адже він поводить себе так само, як і
розбіжний ряд
,
який розбігається за ознакою порівняння
(адже він поводить себе так само, як і
розбіжний ряд
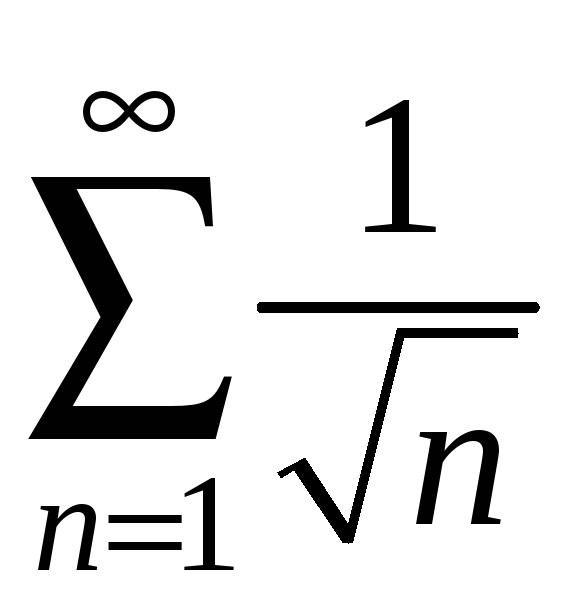 ).
).
При
![]() одержимо ряд з чергуванням знаків
одержимо ряд з чергуванням знаків
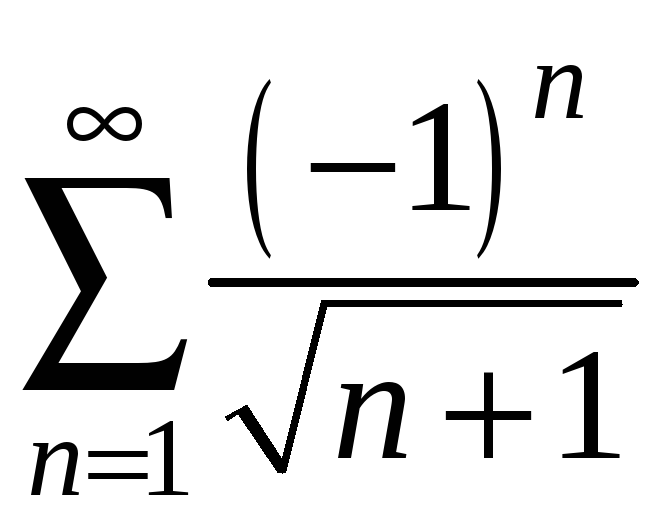 .
Дослідимо його за ознакою Лейбніца: 1)
.
Дослідимо його за ознакою Лейбніца: 1)
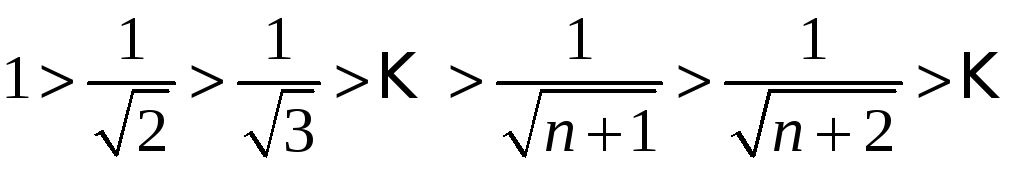 ,
2)
,
2) .
Отже, ряд
.
Отже, ряд
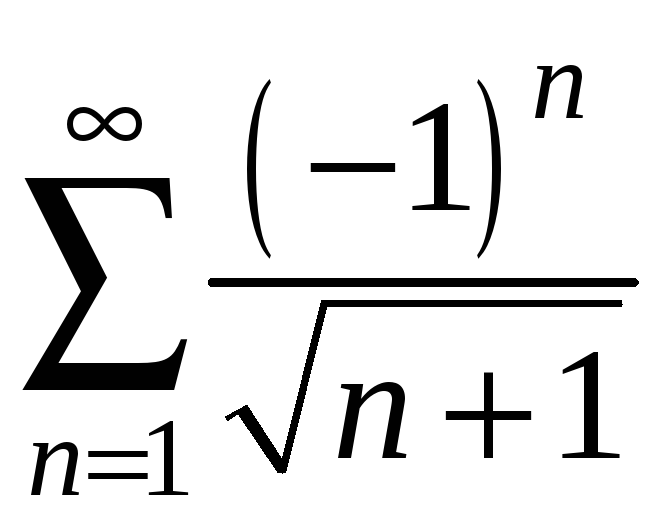 збігається.
збігається.
Таким
чином, область збіжності степеневого
ряду:
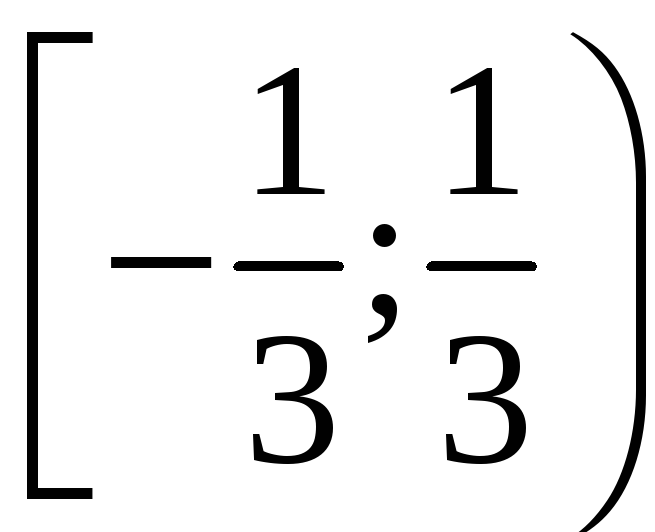 .
.
Зауваження.
1. Існують
ряди, що збігаються при
![]() ( наприклад ряд
( наприклад ряд
 ).
Якщо інтервал збіжності
).
Якщо інтервал збіжності
![]() ,
то вважаємо, що
,
то вважаємо, що
![]() .
.
2. Не
існує рядів, які розбігаються при
![]() .
Хоча б в одній точці
.
Хоча б в одній точці
![]() збігається будь-який степеневий ряд.
Якщо область збіжності містить лише
одну цю точку, то вважаємо, що
збігається будь-який степеневий ряд.
Якщо область збіжності містить лише
одну цю точку, то вважаємо, що
![]() .
.
3. Якби
для дослідження ряду
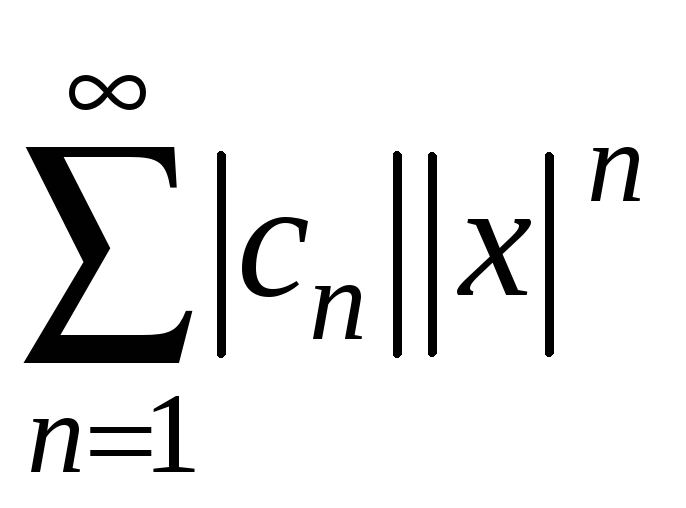 було застосовано ознаку Коші, а не
Даламбера, то для радіуса збіжності
отримали б іншу формулу:
було застосовано ознаку Коші, а не
Даламбера, то для радіуса збіжності
отримали б іншу формулу:
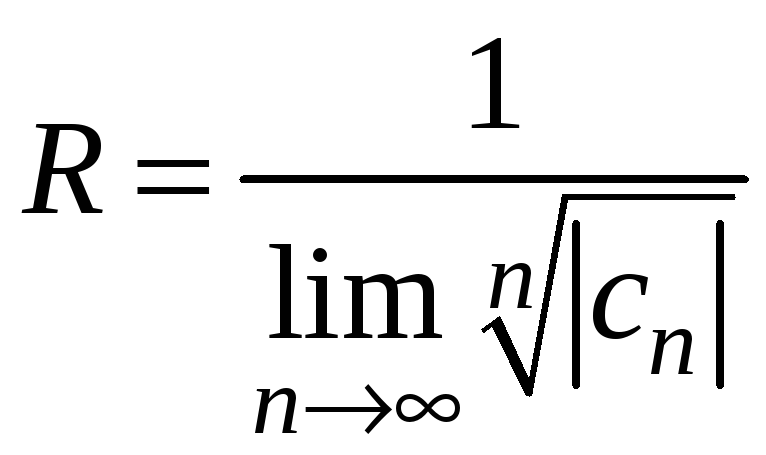 .
.
4. Інтервал
збіжності ряду
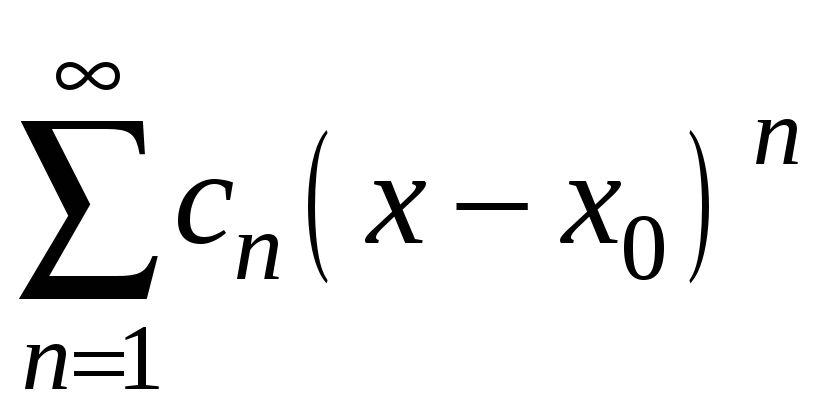 задається нерівністю:
задається нерівністю:
![]() ;
;
![]() ;
;
![]() .
.
Теорема
3.21 Нехай
степеневий ряд
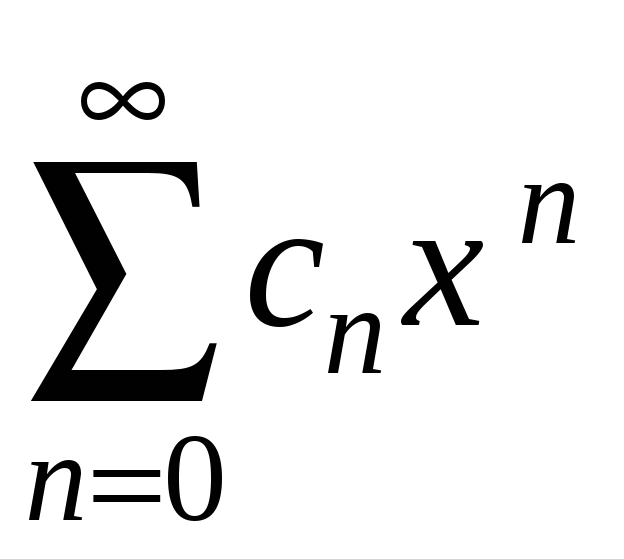 збігається в інтервалі
збігається в інтервалі
![]() ,
тоді він є мажоровним на будь-якому
відрізку
,
тоді він є мажоровним на будь-якому
відрізку
![]() ,
де
,
де
![]() .
.
Доведення.
В інтервалі збіжності
![]() степеневий ряд збігається абсолютно.
Тобто при будь-якому
степеневий ряд збігається абсолютно.
Тобто при будь-якому
![]() числовий ряд
числовий ряд
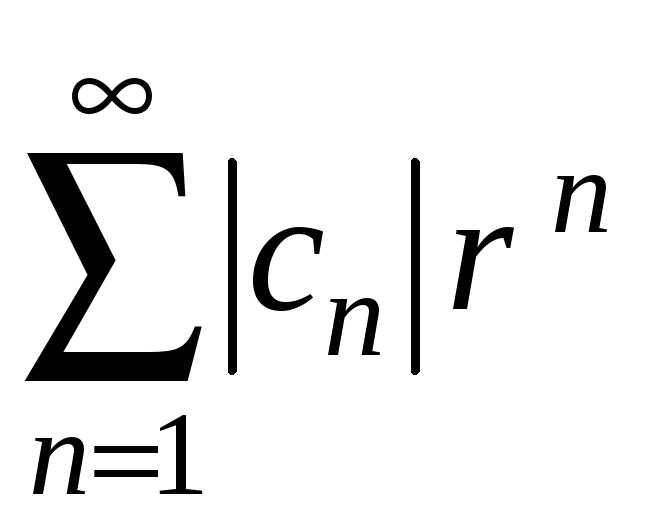 збігається. Але при всіх
збігається. Але при всіх
![]() маємо:
маємо:
![]() ,
,
![]() .
Таким чином, степеневий ряд мажоровний
на відрізку
.
Таким чином, степеневий ряд мажоровний
на відрізку
![]() .
.
Зауважимо, що тоді на степеневий ряд можна перенести всі властивості мажоровних рядів.
Теорема
3.22 Сума
ряду
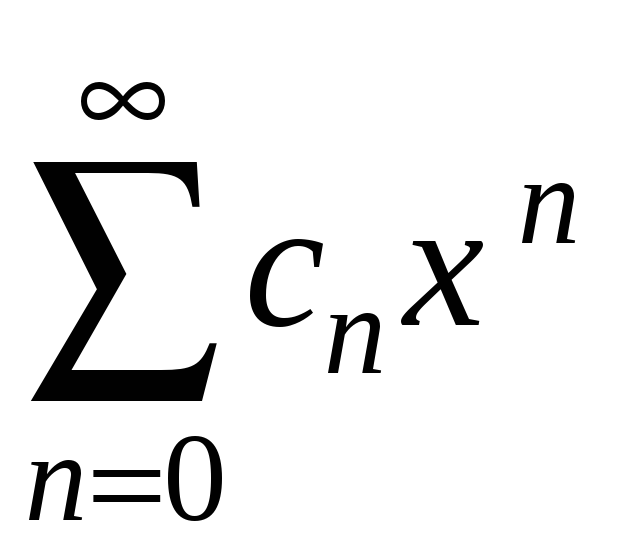 неперервна у будь-якій точці інтервалу
збіжності.
неперервна у будь-якій точці інтервалу
збіжності.
Теорема
3.23 Нехай
степеневий ряд
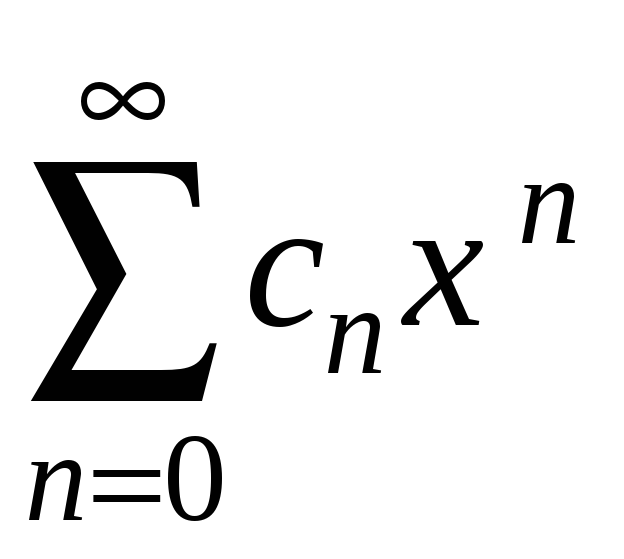 має інтервал збіжності
має інтервал збіжності
![]() і
і
![]() - його сума. Тоді ряд, отриманий його
почленним диференціюванням
- його сума. Тоді ряд, отриманий його
почленним диференціюванням
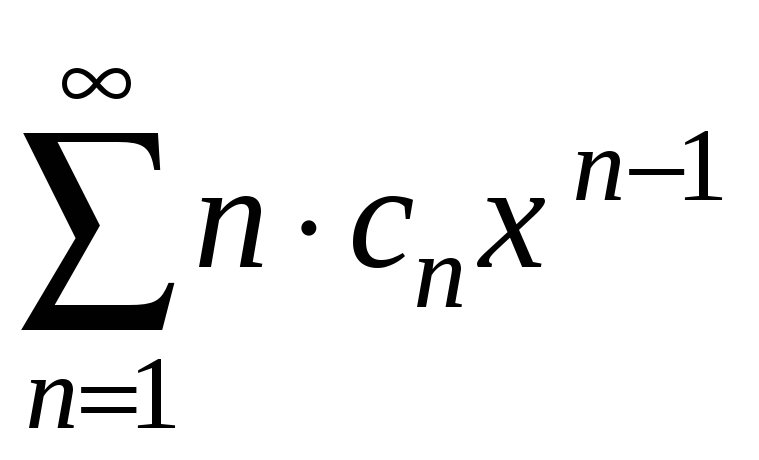 має такий самий інтервал збіжності і
його сума
має такий самий інтервал збіжності і
його сума
![]() ,
,
![]() .
.
Теорема
3.24 Степеневий
ряд можна почленно інтегрувати по
будь-якому проміжку, що лежить всередині
інтервалу збіжності, тобто для будь-яких
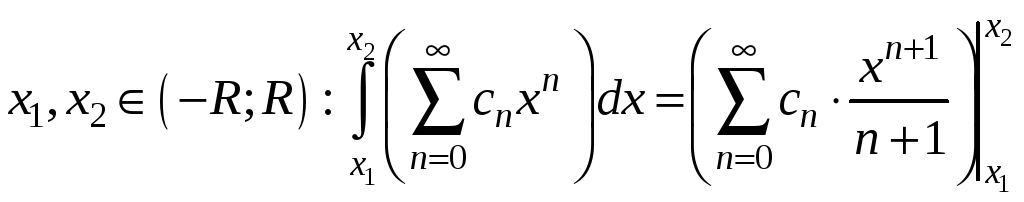 .
.
