§10. Заміна змінної у визначеному інтегралі
Теорема
1.7
Нехай у визначеному інтегралі
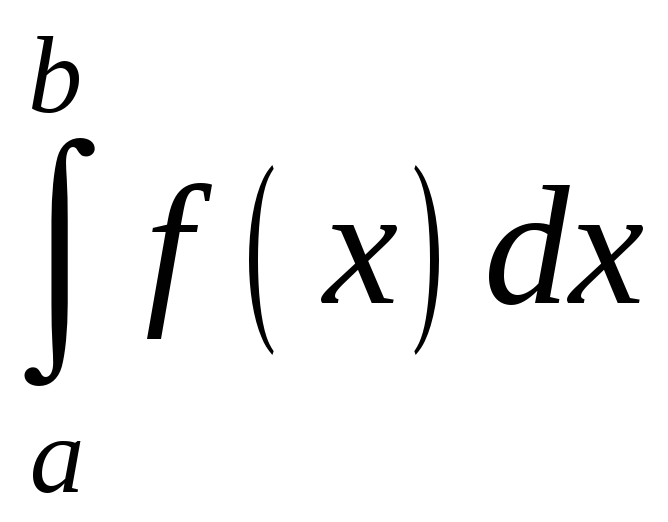функція
неперервна на
.
Введемо нову змінну
за формулою
.
Якщо 1) числа
і
такі, що
;
2) функції
неперервні на відрізку
,
то
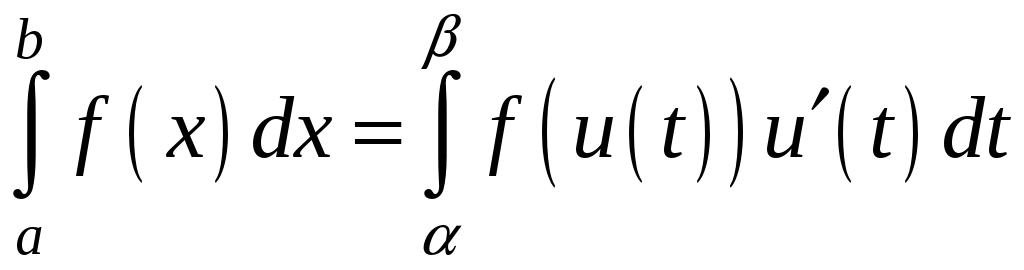
Доведення.
Нехай
первісна функції
на
.
Тоді інтеграл лівої частині рівності
(1.10) обчислимо за формулою Ньютона –
Лейбніца:
.
Доведемо, що і права частина дорівнює
цьому ж числу.
.
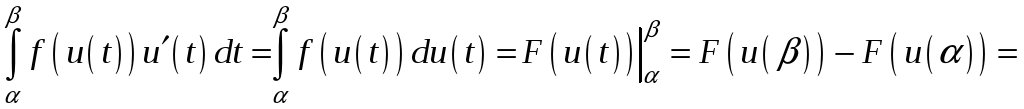
Рівність (1.10) доведена.
Зауважимо,
що при виконанні заміни змінної у
визначеному інтегралі ми не повертаємось
до старої змінної
.
Замість
у первісну
просто підставляємо нові межі інтегрування
і
.
Приклад.
.
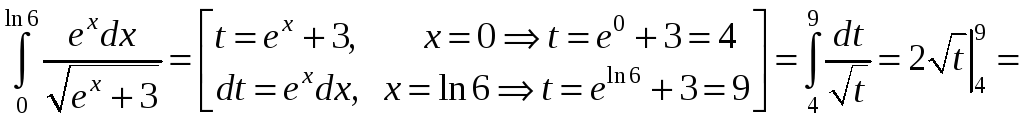
§11. Інтегрування частинами у визначеному інтегралі
Теорема
1.8
Нехай
і
- диференційовні на відрізку
функції тоді:
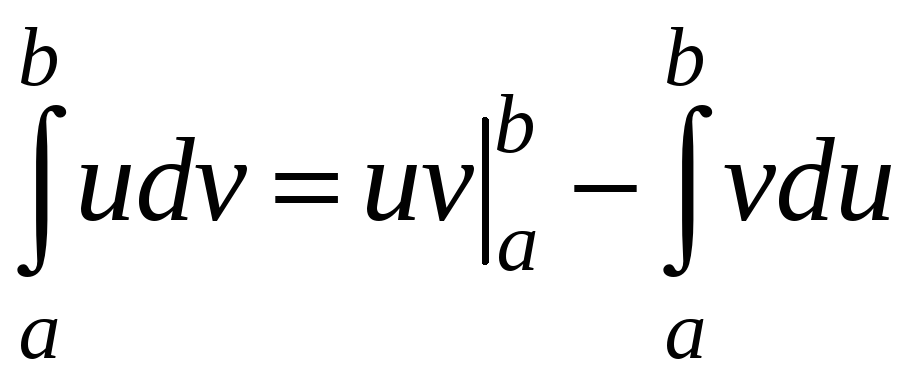
Доведення.
Обчислимо визначений інтеграл
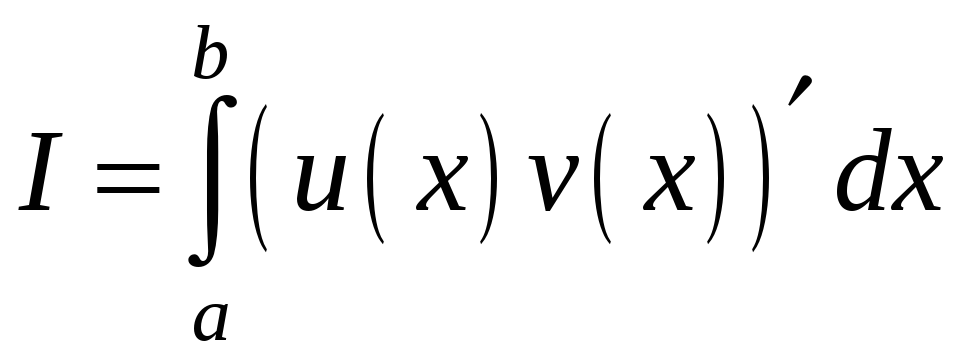за формулою Ньютона – Лейбніца:
.
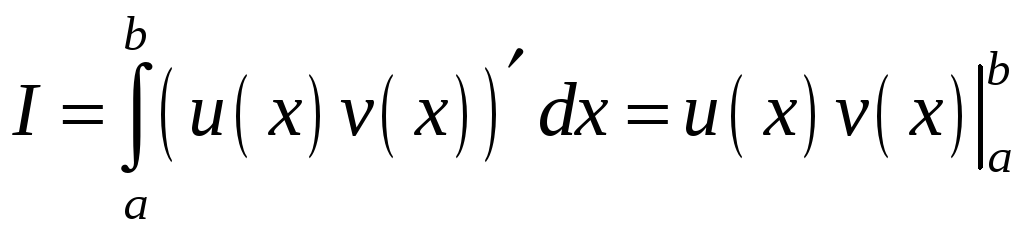З іншого боку маємо:
.
Отже.
.
Це означає, що рівність (1.11) доведена.
Приклад.
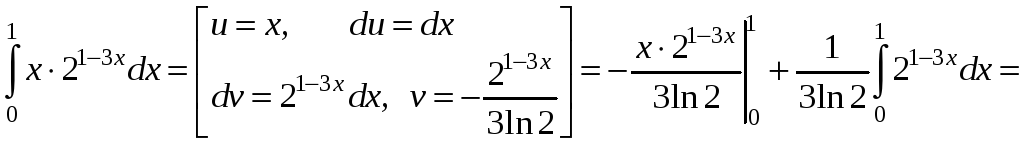
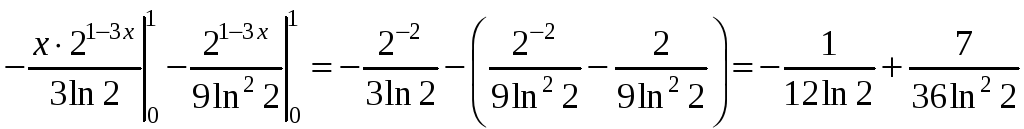
§12. Невластиві інтеграли
1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
Нехай
функція
визначена і неперервна на проміжку
.
Розглянемо інтеграл
.
Він має сенс при будь-якому
.
При змінені
інтеграл змінюється і є неперервною
функцією від
(див. §8).
Означення.
Якщо
існує скінченна границя
,
то її називають невластивим інтегралом
від функції
по проміжку
.
Пишуть
.
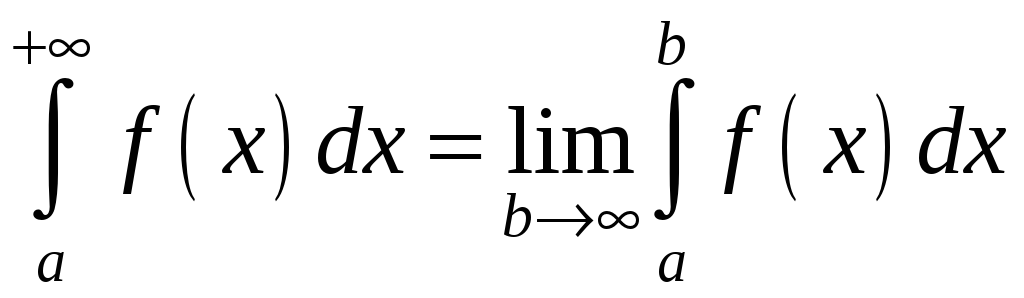Кажуть, що в цьому випадку невластивий інтеграл збігається. Якщо ж скінченної границі не існує, то будемо казати, що інтеграл розбігається.
Аналогічно
визначаються невластиві інтеграли по
іншим нескінченним проміжкам:
;
.
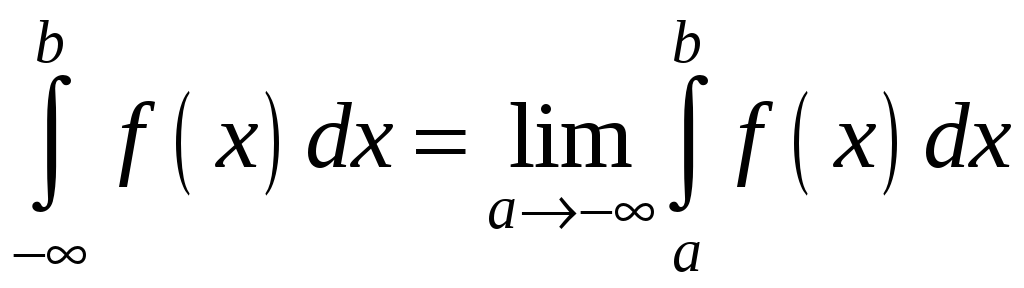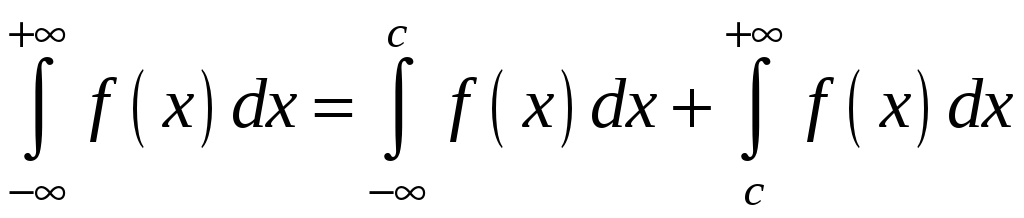Приклад.
1)
;
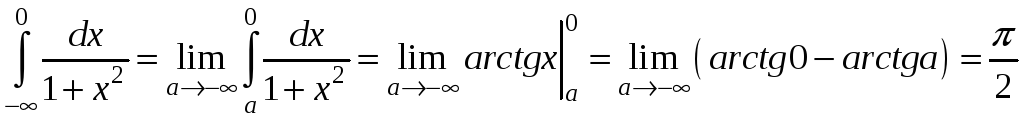2)
.
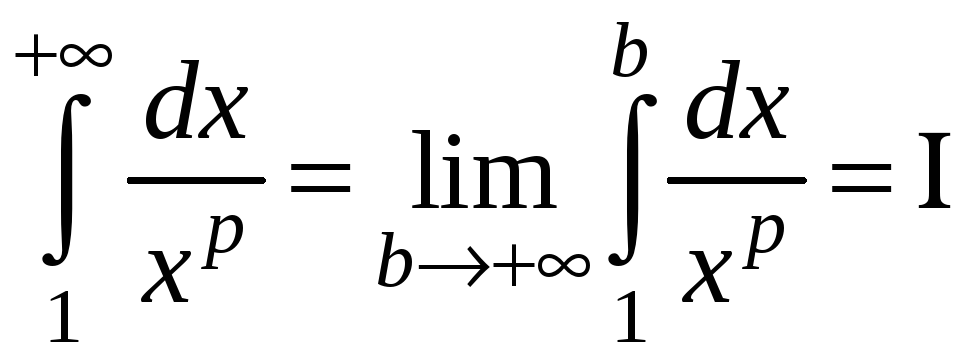Якщо
,
то
.
Якщо
,
то
.
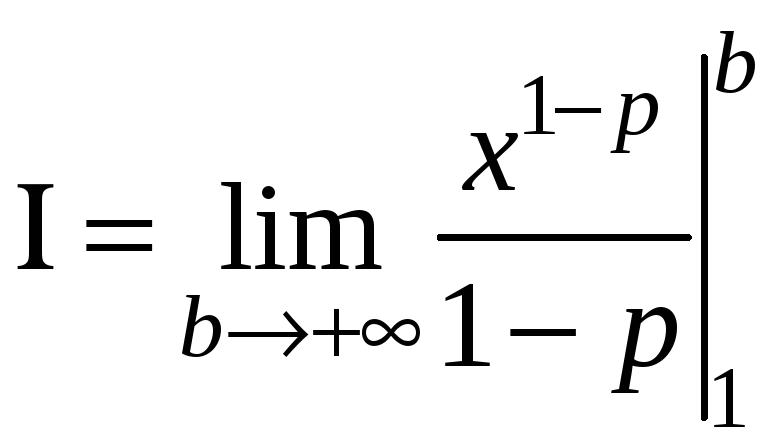При цьому, коли
,
маємо:
,
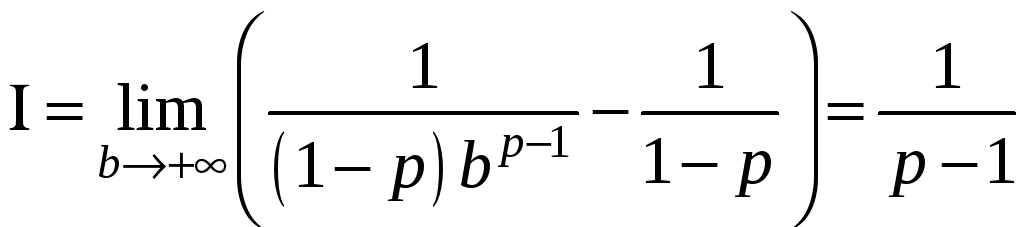а коли
.
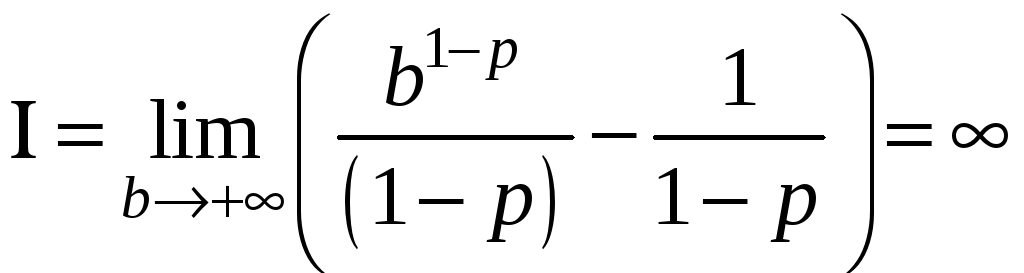Таким чином,
збігається і дорівнює
,
якщо
і розбігається при
.
2. Інтеграли від розривної функції (невластиві інтеграли роду).
Нехай
функція
визначена і неперервна при
,
а в точці
має розрив другого роду. Тоді неможливо
говорити про
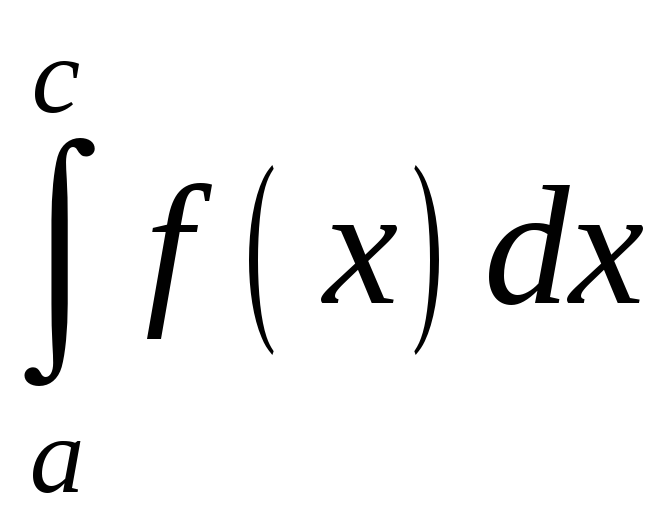як про границю інтегральної суми.
Означення.
Невласний
інтеграл
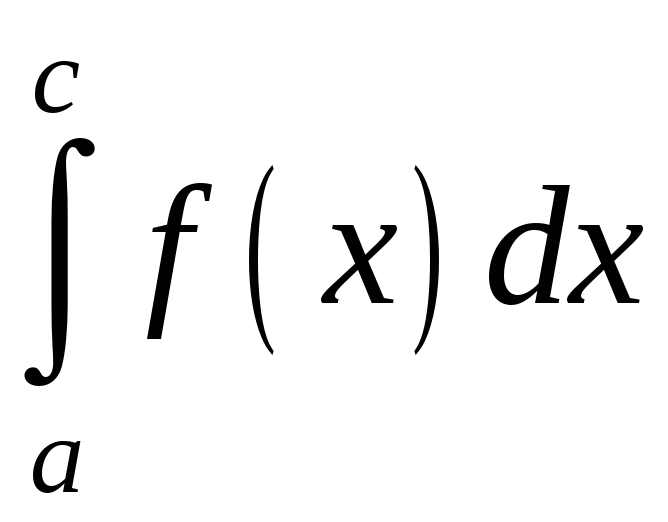в цьому випадку визначається рівністю
.
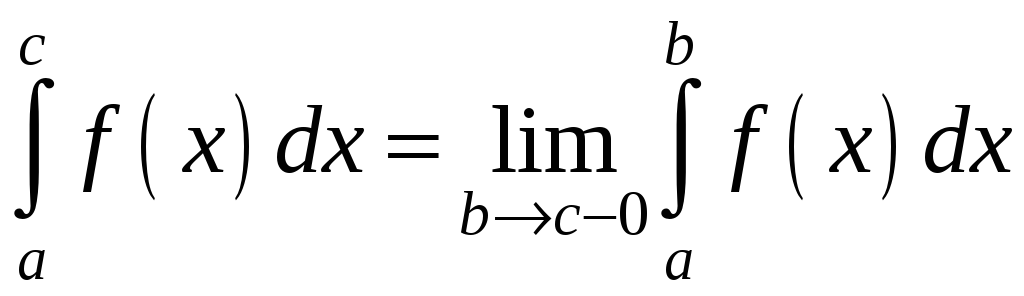Якщо границя в правій частини рівності (1.13) існує і скінченна, то кажуть, що невластивий інтеграл збігається, в супротивному – розбігається.
Якщо
функція
має розрив другого роду на лівому кінці
відрізка
,
то
.
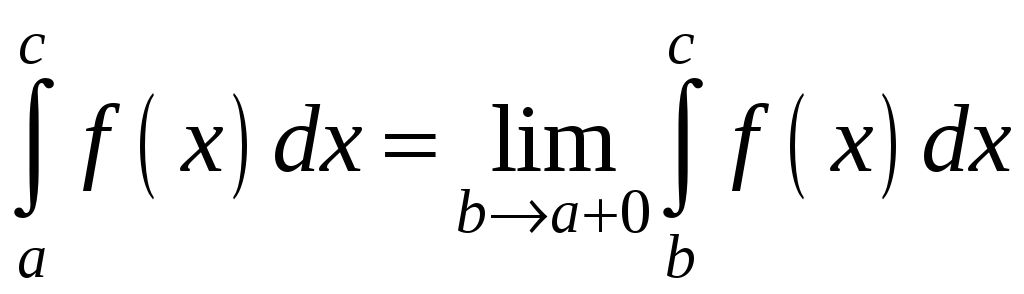Приклад.
.
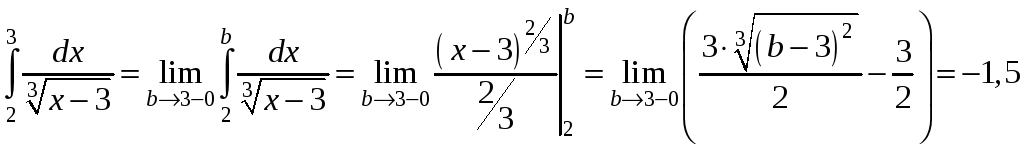Інтеграл збігається.
§12. Застосування визначеного інтеграла
Розглянемо
загальну схему застосування визначеного
інтеграла до практичних задач (так
званий метод диференціалу). Нехай
потрібно знайти значення якої - небудь
геометричної або фізичної величини
,
що пов’язана з відрізком
,
якому належить деяка змінна
.
І. На
відрізку
виберемо довільне значення
і розглянемо змінний відрізок
,
на якому шукана величина
стає функцією
.
Тобто вважаємо, що частина шуканої
величини є невідома функція
.
При цьому
.
ІІ.
Знайдемо головну частину приросту
цієї функції, коли
набуває приросту
.
Тобто знайдемо її диференціал. Маємо:
,
де
-
функція, що визначається згідно з умовами
задачі.
ІІІ.
Вважаючи, що
при
знаходимо шукану величину шляхом
інтегрування
в межах від
до
:
.