
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
§6. Розвинення функції в степеневий ряд.
Нехай
функція
![]() є сумою степеневого ряду
є сумою степеневого ряду
 .
Тобто в інтервалі
.
Тобто в інтервалі
![]() виконано рівність:
виконано рівність:
![]() .
.
![]()
Назвемо
цю рівність розвиненням функції
![]() в ряд по степеням
в ряд по степеням
![]() .
Нехай функція
.
Нехай функція
![]() в кожній точці інтервалу
в кожній точці інтервалу
![]() має похідні будь-якого порядку. Оскільки
степеневий ряд можна почленно
диференціювати в кожній точці інтервалу
збіжності, то продиференціювавши обидві
частини рівності (3.8), маємо:
має похідні будь-якого порядку. Оскільки
степеневий ряд можна почленно
диференціювати в кожній точці інтервалу
збіжності, то продиференціювавши обидві
частини рівності (3.8), маємо:
![]() .
.
Можна продиференціювати обидві частини рівності (3.8) скільки завгодно разів.
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() .
.
Підставивши
в ці рівності і в рівність (3.8)
![]() замість
замість
![]() отримаємо:
отримаємо:
![]()
Таким чином,
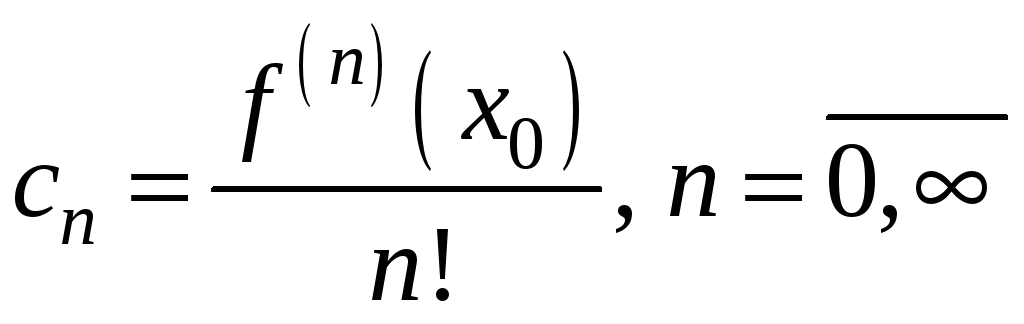 .
.
![]()
Отже, справедлива
Теорема
3.25 Якщо
функція
![]() допускає розвинення в степеневий ряд
в інтервалі
допускає розвинення в степеневий ряд
в інтервалі
![]() ,
то це розвинення єдине.
,
то це розвинення єдине.
Тобто
коефіцієнти розвинення функції
![]() в ряд по степеням
в ряд по степеням
![]() однозначно знаходяться за формулами
(3.9).
однозначно знаходяться за формулами
(3.9).
Ряд
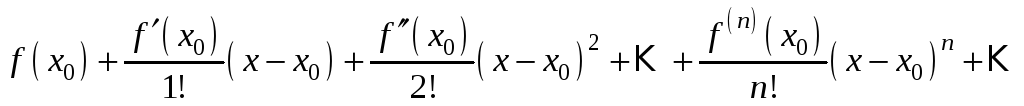
![]()
називають
рядом Тейлора для функції
![]() .
.
Якщо
![]() ,
то ряд (3.10) набуває вигляду:
,
то ряд (3.10) набуває вигляду:
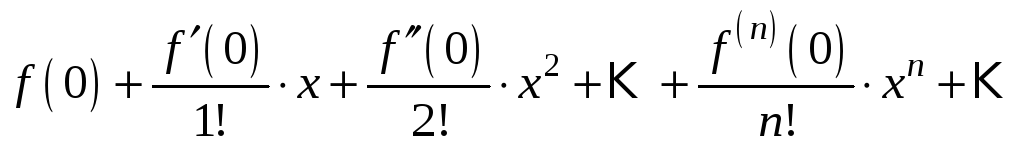 .
.
Він
називається рядом Маклорена для функції
![]() .
.
Як
бачимо, ряд Тейлора можна побудувати
для будь-якої функції, яка диференційовна
скільки завгодно разів в деякому околі
точки
![]() .
Але знак рівності між самою функцією і
її рядом Тейлора можна поставити не
завжди. Якщо
.
Але знак рівності між самою функцією і
її рядом Тейлора можна поставити не
завжди. Якщо
![]() -
-
![]() - на часткова сума ряду Тейлора,
- на часткова сума ряду Тейлора,
![]() - сума залишку після
- сума залишку після
![]() - ного члена, то рівність
- ного члена, то рівність
![]() виконана лише в тому випадку, коли
виконана лише в тому випадку, коли
![]() (адже
(адже
![]() ).
).
Теорема
3.26 Ряд
Тейлора представляє задану функцію
![]() тільки тоді, коли
тільки тоді, коли
![]() .
.
Розвинення деяких функцій в ряд Маклорена.
1. Запишемо
ряд Маклорена для функції
![]() .
Враховуючи, що
.
Враховуючи, що
![]() ,
тобто
,
тобто
![]()
![]() .
Маємо:
.
Маємо:
 .
Знайдемо радіус збіжності цього ряду
.
Знайдемо радіус збіжності цього ряду
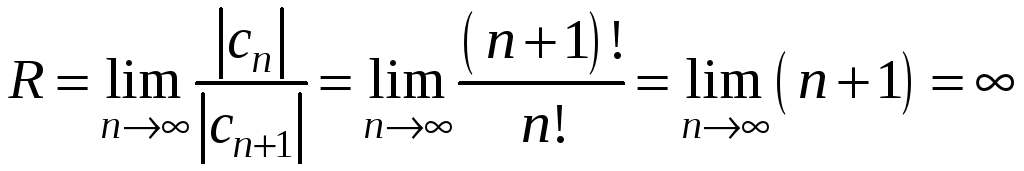 .
Тоді область збіжності:
.
Тоді область збіжності:
![]() .
.
Оцінимо
залишок ряду
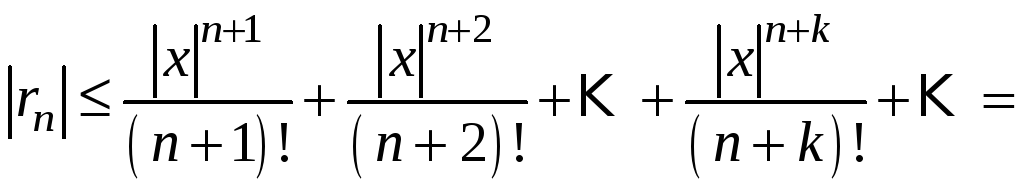
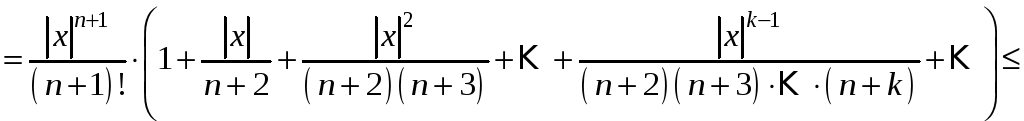
 .
Вважаючи, що
.
Вважаючи, що
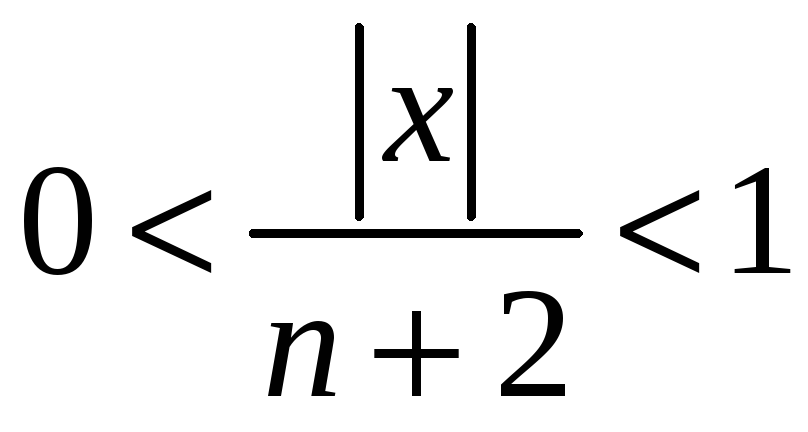 (адже
(адже
![]() - скінченне число, а
- скінченне число, а
![]() )
в правій частині нерівності маємо
геометричний ряд, сума якого дорівнює
)
в правій частині нерівності маємо
геометричний ряд, сума якого дорівнює
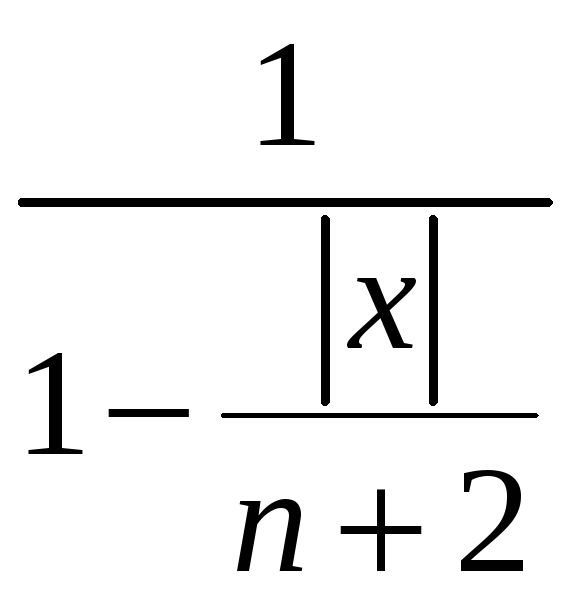 .
.
Тоді
 .
Таким чином,
.
Таким чином,
![]() коли
коли
![]() .
Отже при
.
Отже при
![]() справедливе розвинення:
справедливе розвинення:
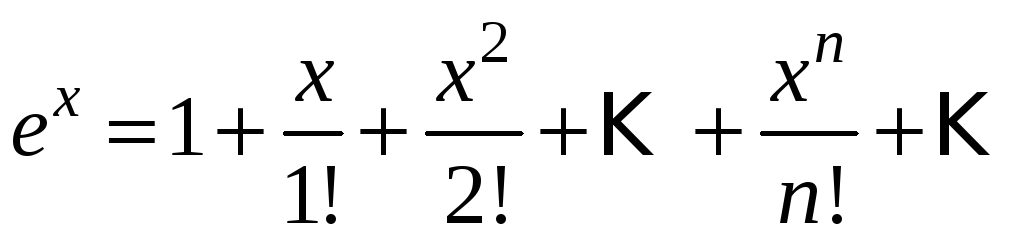
![]()
2. Аналогічно можна отримати розвинення:
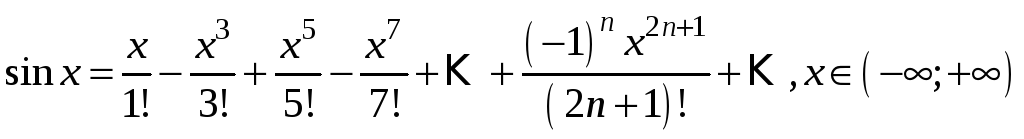 .
.
![]()
3. Продиференціювавши обидві частини рівності (3.12) одержимо рівність:
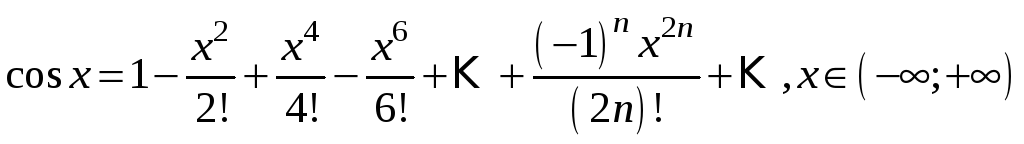 .
.
![]()
4.
Розвинення функції
![]() ,
називають біноміальним. Обчислимо його
коефіцієнти:
,
називають біноміальним. Обчислимо його
коефіцієнти:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Отже біноміальний ряд має вигляд:
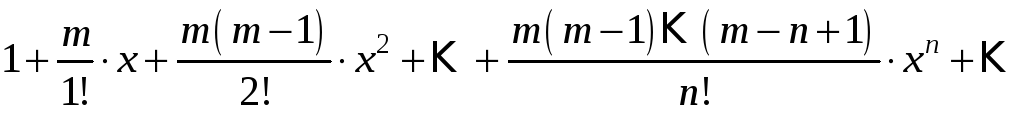 .
.
Обчислимо його радіус збіжності
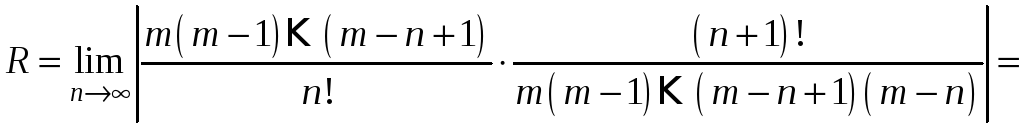
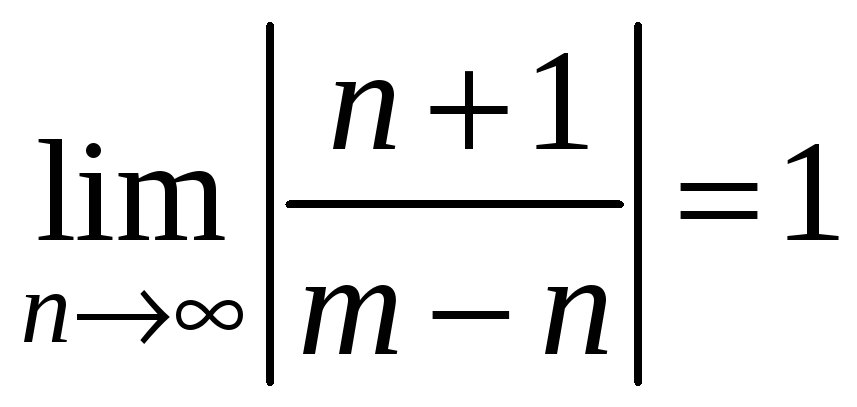 .
Отже біноміальний ряд має інтервал
збіжності
.
Отже біноміальний ряд має інтервал
збіжності
![]() .
Можна довести, що
.
Можна довести, що
![]() при
при
![]() .
Тоді одержимо рівність
.
Тоді одержимо рівність

![]()
Поведінка
ряду на межах інтервалу залежить від
того, яким числом є показник степеня
![]() .
.
Зауважимо,що
коли
![]() -
натуральне число, біноміальний ряд стає
многочленом (адже коефіцієнти при всіх
вищих за
-
натуральне число, біноміальний ряд стає
многочленом (адже коефіцієнти при всіх
вищих за
![]() степенях
степенях
![]() нульові), а формула (3.14) перетворюється
на формулу бінома Ньютона
нульові), а формула (3.14) перетворюється
на формулу бінома Ньютона
 .
.
5. Запишемо
розвинення функції
![]() за формулою (3.14):
за формулою (3.14):
![]() .
.
![]()
Проінтегруємо
обидві частини цієї рівності в межах
від
![]() до
до
![]() .
Отримаємо:
.
Отримаємо:
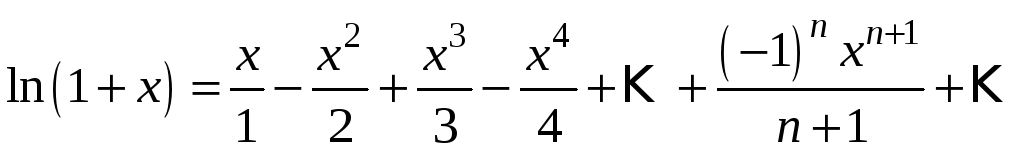 .
.
![]()
Область
збіжності:
![]() .
.
6. Якщо
в формулі (3.15) замінити
![]() на
на
![]() і також проінтегрувати обидві частини,
то отримаємо розвинення функції
і також проінтегрувати обидві частини,
то отримаємо розвинення функції
![]() .
.
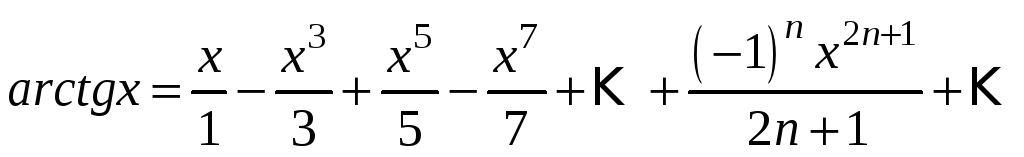 .
.
![]()
Область
збіжності:
![]() .
.
Розглянемо деякі приклади застосування степеневих рядів до наближених обчислень.
Приклад.
Обчислити наближене значення функції
![]() в точці
в точці
![]() з точністю
з точністю
![]() .
.
Розв’язання.
Скористаємось розвиненням (3.11) при
![]() .
Отримаємо:
.
Отримаємо:
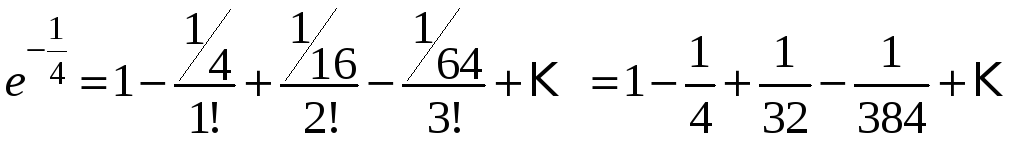 .
Зауважимо, що
.
Зауважимо, що
![]() ,
а
,
а
![]() .
Замінимо суму ряду сумою перших трьох
його членів
.
Замінимо суму ряду сумою перших трьох
його членів
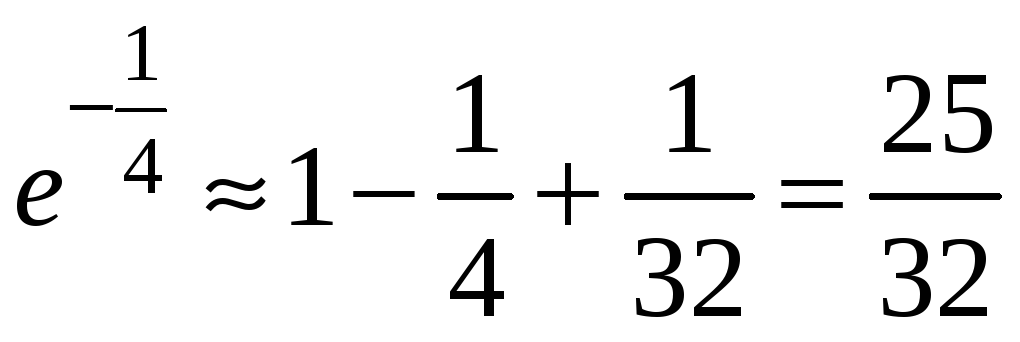 .
Цей числовий ряд задовольняє умови
ознаки Лейбніца, тому похибка наближення
не перевищує модуля першого відкинутого
члена ряду
.
Цей числовий ряд задовольняє умови
ознаки Лейбніца, тому похибка наближення
не перевищує модуля першого відкинутого
члена ряду
 .
Отже, потрібна точність забезпечена.
.
Отже, потрібна точність забезпечена.
Приклад.
Обчислити наближено визначений інтеграл
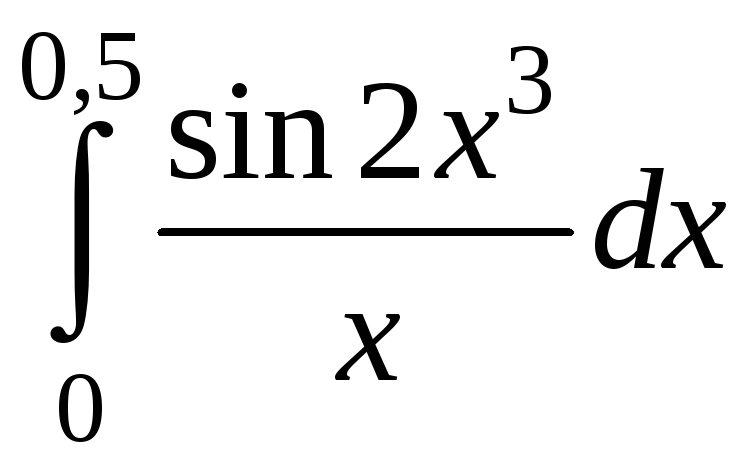 ,
розклавши підінтегральну функцію в ряд
по степеням
,
розклавши підінтегральну функцію в ряд
по степеням
![]() і проінтегрувавши перші два його члени.
Оцінити похибку.
і проінтегрувавши перші два його члени.
Оцінити похибку.
Розв’язання.
Зауважимо, що первісна функції
 не виражається через елементарні
функції, тобто цей інтеграл не може бути
обчислений методами розглянутими в
розділі
не виражається через елементарні
функції, тобто цей інтеграл не може бути
обчислений методами розглянутими в
розділі
![]() .
Скориставшись формулою (3.12), маємо:
.
Скориставшись формулою (3.12), маємо:

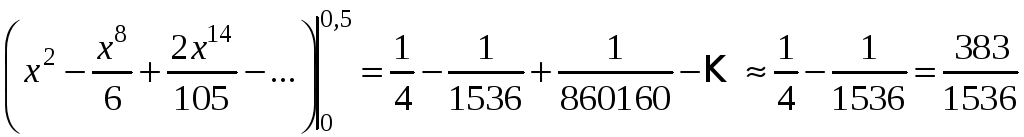 .
Оцінимо похибку наближення:
.
Оцінимо похибку наближення:
![]() .
.
Приклад.
Записати три перших відмінних від нуля
члени розвинення в ряд по степеням
![]() розв’язку задачі Коші:
розв’язку задачі Коші:
![]() .
.
Розв’язання.
Як бачимо, це диференціальне рівняння
не можна віднести до жодного з розглянутих
у розділі
![]() типів, тому ми не маємо можливості знайти
його загальний розв’язок. Будемо шукати
розв’язок задачі Коші
типів, тому ми не маємо можливості знайти
його загальний розв’язок. Будемо шукати
розв’язок задачі Коші
![]() у вигляді ряду Маклорена:
у вигляді ряду Маклорена:
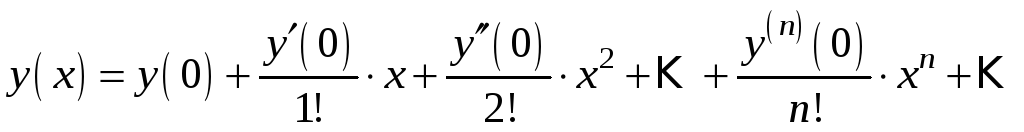 .
.
Перші
два члена задаються початковою умовою
![]() і диференціальним рівнянням
і диференціальним рівнянням
![]() ,
,
![]() .
Продиференціюємо обидві частини
диференціального рівняння. Одержимо:
.
Продиференціюємо обидві частини
диференціального рівняння. Одержимо:
![]() ;
;
![]() .
.
Тоді
розв’язок задачі Коші має вигляд:
![]() або
або
![]() .
.
Для
більш детального вивчення рядів
рекомендуємо звернутись до підручників
![]() .
.
Література
-
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов, т.1, 2, – М.: Наука, 1970-1985.
-
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики, - М.: Наука, 1975.
-
Двайт Г.Б. Таблицы интегралов, - М.: Наука, 1977.
-
Кудрявцев Л.Д. Краткий курс математического анализа, - М.: Наука, 1989.
-
Степанов В.В. Курс дифференциальных уравнений, - М.: Наука, 1958.
-
Матвеев Н.М. Ряды – Ленинград, 1972.
