§3. Інтегрування частинами у невизначеному інтегралі

Теорема 1.3 Для будь-яких двох диференційовних функцій та справедлива рівність

.

Доведення. За однією з властивостей диференціалу маємо:

або .

Проінтегруємо обидві частини останньої рівності. Одержимо

, що і треба довести.

Основними типами інтегралів, для яких є доцільним застосування методу інтегрування частинами є:

1. ;

2.

.

Тут і - многочлен степеня .

Зауваження. В перших трьох інтегралах за треба взяти , а в решті інтегралів – відповідну трансцендентну функцію, тобто .

Приклади.

1)

;

2)

.

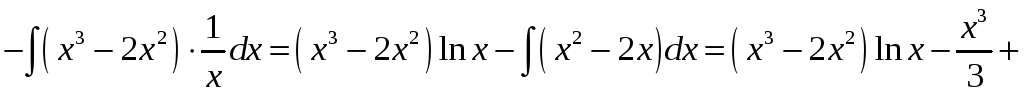
§4. Інтегрування деяких виразів, що містять квадратний тричлен

1. Розглянемо спочатку інтеграли виду 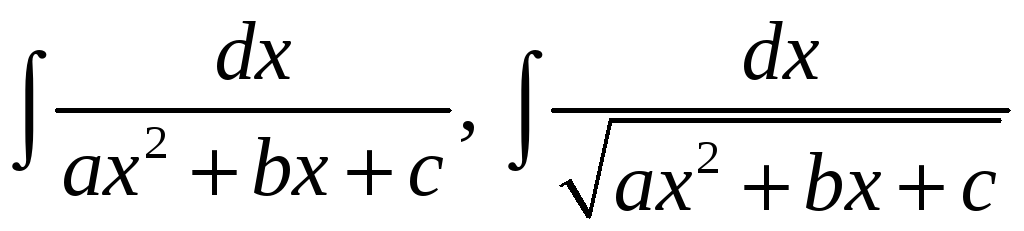. Якщо у квадратному тричлені винести за дужки старший коефіцієнт та доповнити вираз до повного квадрату, то після підведення під знак диференціала виразу одержимо один з табличних інтегралів виду 8-11.

Приклади.

1)

;

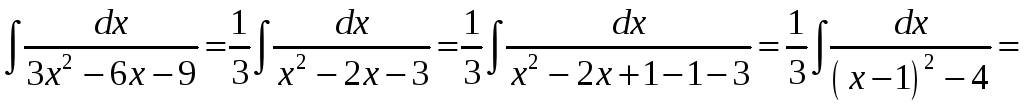
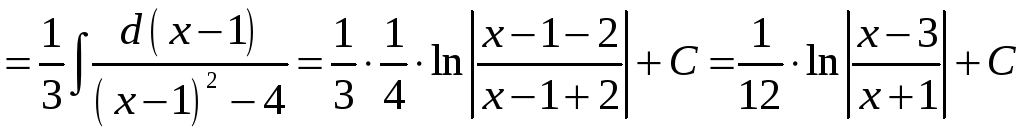2)

.

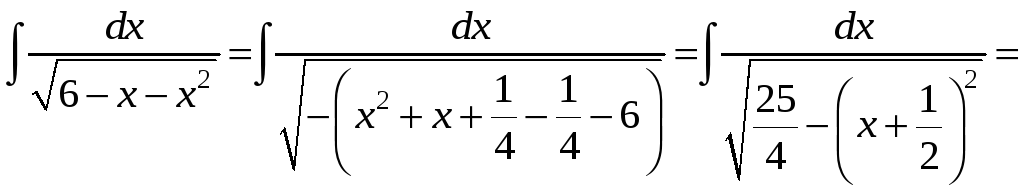
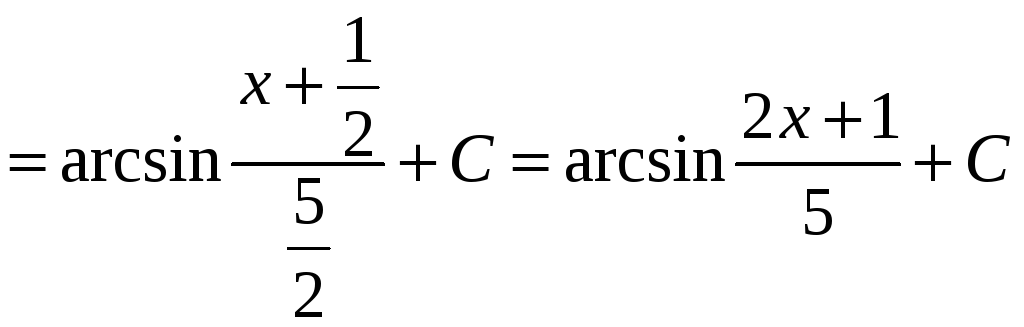2. Інтеграли виду 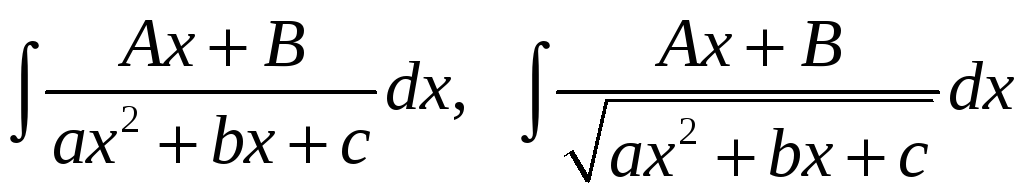легко обчислюються у випадку, коли . Тоді можна скористатися формулою або .

Приклад.

.

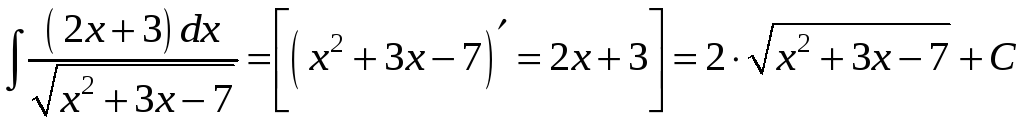В загальному випадку можна чисельник розділити з остачею на і звести цей випадок до вже розглянутих.

Приклад.

.

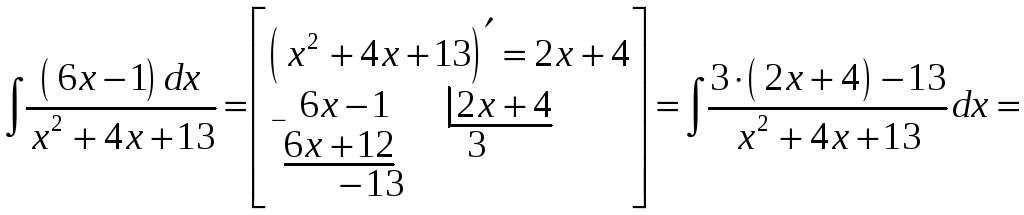
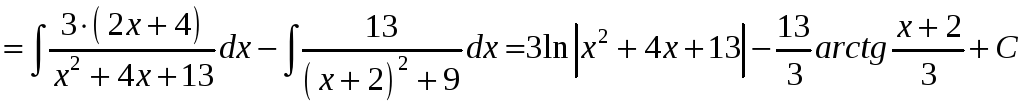§5. Інтегрування деяких ірраціональних і тригонометричних виразів

1. Якщо підінтегральна функція представляє собою частку двох многочленів відносно , то за допомогою заміни , де є найменшим спільним кратним чисел , в цьому виразі можна звільнитись від ірраціональності.

Приклад.

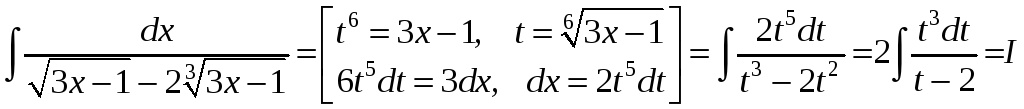
Розділимо чисельник на знаменник з остачею, щоб перетворити підінтегральну функцію на суму многочлена і дробу зі знаменником і остачею в чисельнику. Одержимо: . Тоді

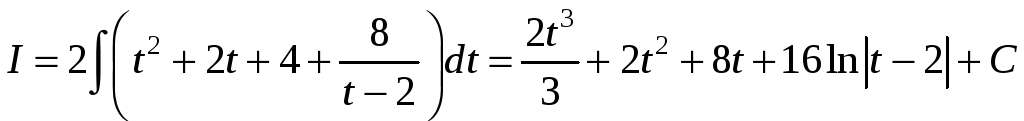, де .

2. Нехай підінтегральна функція має вигляд , де хоча б один з показників степеня ( або ) є непарний. Тоді при непарному застосовують підстановку , а при непарному - .

Приклад.

.

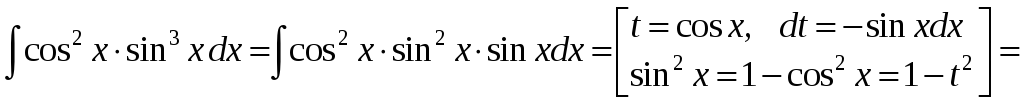
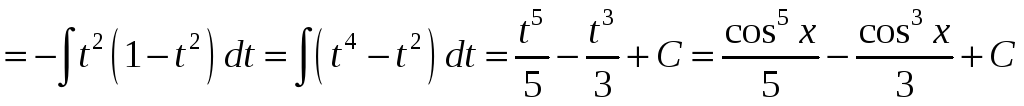3. Якщо у виразі , обидва показники степеня парні, то застосовуючи формулу подвійного аргументу або формули зниження степеня , такий інтеграл зводять до табличного, або до такого, який розглянуто у пункті 2 цього параграфу.

Приклад.

.

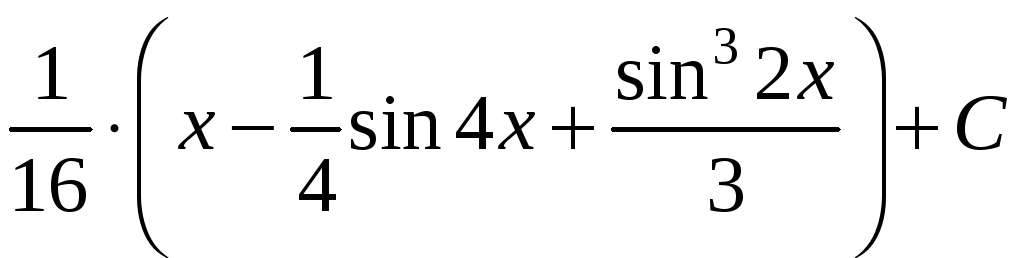§6. Про функції, інтеграли від яких не виражаються через елементарні функції

Нами було розглянуто лише декілька видів функцій до яких можуть бути застосовані методи інтегрування з метою обчислення їх первісних. Деякі види таких інтегралів студенти можуть навчитись обчислювати самостійно ([1], [2] ) або можуть скористатися таблицями, наприклад, [3].

Можна довести: будь-яка функція, що є неперервною на проміжку , має на цьому проміжку первісну. Але не завжди ця первісна може бути виражена через елементарні функції. Такими є первісні, що виражаються інтегралами та багато інших.

§7. Визначений інтеграл та його властивості

Розглянемо спочатку геометричну задачу, яка приводить до поняття визначеного інтегралу. Криволінійною трапецією назвемо фігуру, що обмежена лініями , де - неперервна і невід’ємна на функція (рис.1). Треба знайти площу цієї фігури.

Розіб’ємо відрізок точками на частинні відрізки довжиною . Таким чином розбиваємо криволінійну трапецію на вертикальних смужок. Знайдемо площу кожної з них. Візьмемо на кожному з частинних проміжків по одній довільній точці і обчислимо - значення функції в цій точці. Добуток з геометричної точки зору дорівнює площі прямокутника, одна зі сторін якого співпадає з відрізком осі , а друга має довжину . Цей прямокутник зображено на рисунку 1 пунктиром. Як бачимо, площа прямокутника наближено дорівнює площі відповідної смужки криволінійної трапеції. Підсумувавши площі всіх таких прямокутників одержимо наближене значення площі криволінійної трапеції. Тобто

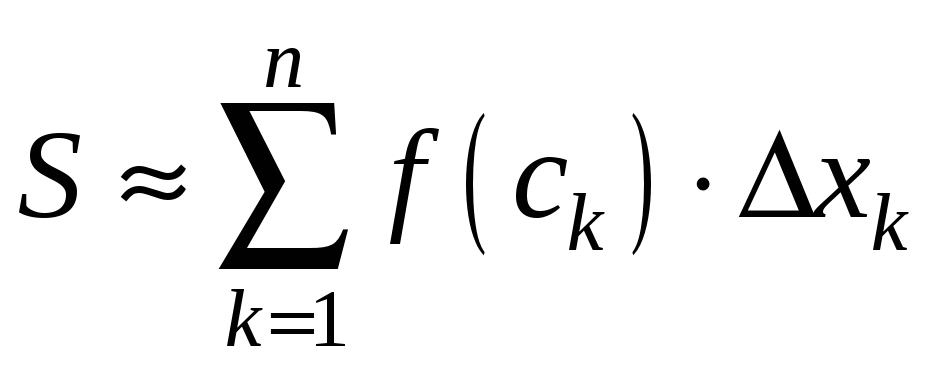. Позначимо через довжину найбільшого з частинних відрізків, назвемо рангом розбиття. Точне значення площі криволінійної трапеції дорівнює границі

.

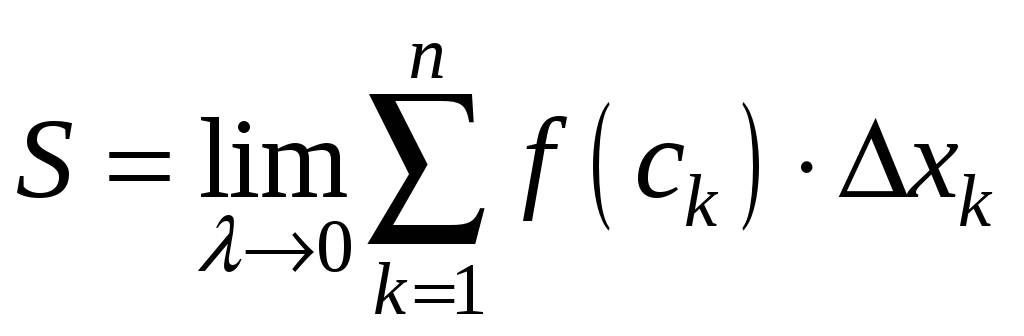Отже, задача про обчислення площі криволінійної трапеції приводить до математичного виразу (1.6), який називається визначеним інтегралом. Дамо точне означення цього поняття.

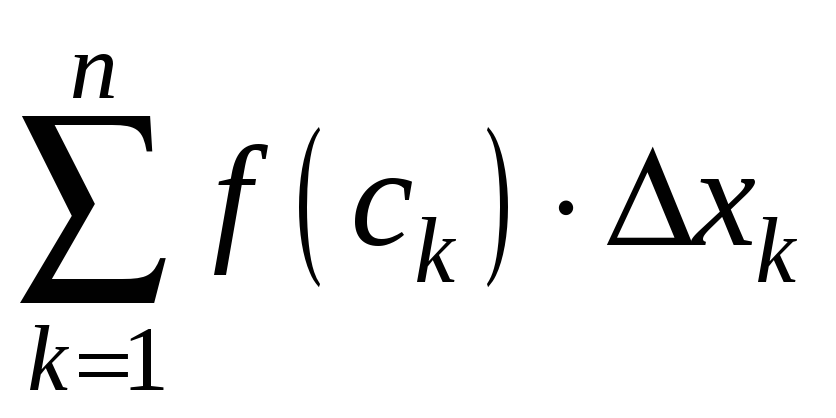Означення. Нехай функція задана на відрізку . Розіб’ємо відрізок точками на частинні відрізки і знайдемо їх довжини . Рангом розбиття назвемо величину, що визначається рівністю . Візьмемо на кожному з відрізків довільну точку , обчислимо - значення функції в цій точці і знайдемо добуток . Складемо суму . Її називають інтегральною сумою або сумою Рімана. Вона, звичайно, залежить від способу розбиття відрізка і вибору проміжних точок . Обчислимо границю інтегральної суми, коли ранг розбиття прямує до нуля. Якщо ця границя існує, скінченна, не залежить від способу розбиття відрізка і вибору проміжних точок, то вона називається визначеним інтегралом від функції по проміжку . Пишуть 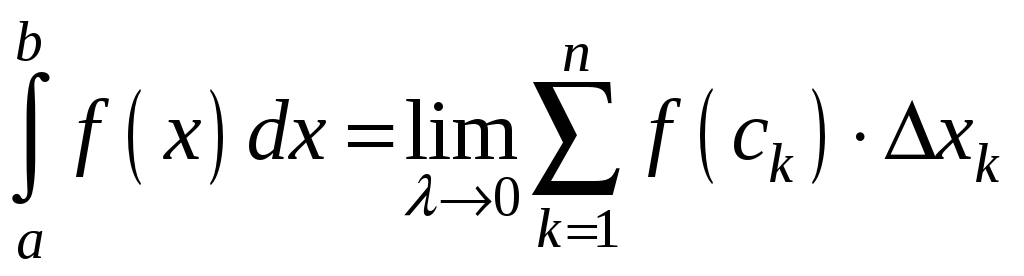. Функція називається підінтегральною функцією, вираз - підінтегральним виразом, числа і - відповідно нижньою та верхньою межами інтегрування.

Теорема 1.4 (Рімана). Якщо функція неперервна на відрізку , то визначений інтеграл 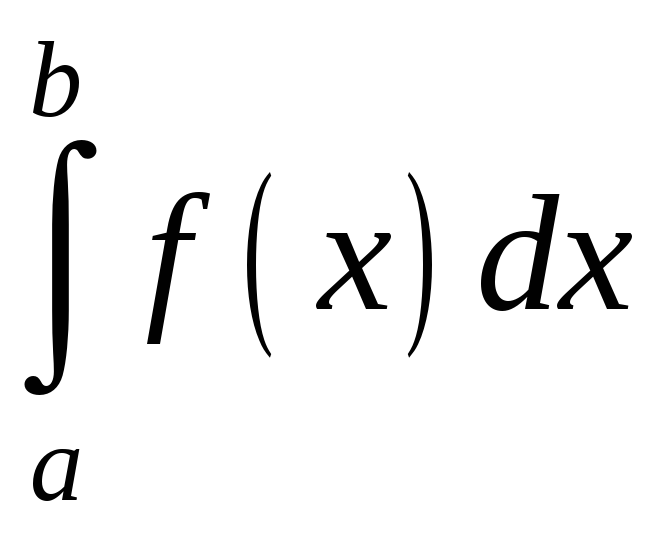існує.