
- •1. Общая характеристика цифровых фильтров
- •1.1. Свойства цифровых фильтров
- •1.2. Представление цифрового фильтра в виде разностного уравнения
- •2. Ких-фильтры. Методы синтеза
- •2.1. Прямоугольное окно
- •2.2. Обобщенное окно Хэмминга
- •2.3. Окно Блэкмана
- •2.4. Окно Кайзера
- •3. Бих-фильтры. Методы синтеза
- •3.1. Аналоговые фильтры-прототипы
- •3.1.1. Фильтры Баттерворта
- •3.1.2. Фильтры Чебышева
- •3.1.3. Эллиптические фильтры
- •3.1.4. Фильтры Бесселя
- •3.2. Методы дискретизации аналогового фильтра
- •3.2.1. Метод инвариантного преобразования импульсной характеристики
- •3.2.2. Метод билинейного преобразования
- •3.3. Преобразования полосы частот для аналоговых фильтров
- •3.4. Преобразование полосы для цифровых фильтров
- •4. Методы реализации цифровых фильтров
- •4.1. Прямая форма
- •4.2. Прямая каноническая форма
- •4.3. Каскадная форма
- •4.4. Параллельная форма
- •5. Работа в среде matlab
- •5.1. Ввод матриц
- •5.2. Матричные операции
- •5.3. Операторы, выражения и переменные
- •5.4. Функции построения матриц
- •5.5. Операторы for, while, if
- •5.6. Скалярные функции
- •5.7. Векторные функции
- •5.8. Mатричные функции
- •5.9. Подматрицы и форма записи с двоеточием
- •5.10. M-файлы
- •5.11. Текстовые строки, сообщения об ошибках, ввод данных
- •5.12. Сравнение эффективности алгоритмов
- •5.13. Формат вывода
- •5.14. Протокол
- •5.15. Графика
- •6. Записная книжка matlab для Microsoft Word
- •6.1. Начало работы
- •6.2. Краткий пример использования Записной книжки
- •7. Проектирование цифровых фильтров в среде matlab
- •Filtic – cоздание начального состояния для функции filter:
- •Freqs – частотная характеристика аналогового фильтра:
- •Freqspace – формирование последовательности отсчетов частоты:
- •Freqz – частотная характеристика цифрового фильтра.
- •Grpdelay – групповая задержка цифрового фильтра:
- •Impz – импульсный отклик цифрового фильтра:
- •Unwrap – корректировка фазовых углов:
- •Zplane – отображение нулей и полюсов цифрового фильтра:
- •7.2. Проектирование цифровых бих-фильтров besself – проектирование аналогового фильтра Бесселя:
- •Butter – проектирование цифрового и аналогового фильтров Баттерворта:
- •Cheby1 – проектирование цифрового и аналогового фильтров Чебышева – первого типа:
- •Cheby2 – проектирование цифрового и аналогового фильтров Чебышева второго типа:
- •Ellip – проектирование эллиптического цифрового и аналогового фильтров:
- •Yulewalk – проектирование рекурсивного фильтра с использованием метода наименьших квадратов по заданной амплитудно-частотной характеристике:
- •7.3. Выбор порядка бих-фильтра buttord – выбор порядка фильтра Баттерворта:
- •Cheb1ord – выбор порядка для фильтра Чебышева первого порядка:
- •Cheb2ord– выбор порядка для фильтра Чебышева первого порядка:
- •Ellipord – выбор порядка эллиптического фильтра:
- •7.4. Проектирование ких-фильтров fir1 – фильтр fir проектируется с использованием метода окна:
- •Fir2– проектирование фильтра fir с использованием оконного метода для произвольной формы фильтра:
- •Firls – проектирование ких-фильтра с использованием минимизации ошибок методом наименьших квадратов (мнк):
- •Intfilt – расчет интерполирующего ких-фильтра:
- •Remez – синтез оптимального fir-фильтра с равномерной (чебышевской) аппроксимацией на основе алгоритма Паркса – Мак-Клелана:
- •7.5. Преобразования czt–z-преобразование по спиральному контуру:
- •Dct– дискретное косинусное преобразование:
- •Impinvar – метод инвариантной импульсной характеристики для перевода аналогового фильтра в цифровой:
- •8. Примеры проектирования цифровых фильтров
- •8.1. Генерация входной последовательности сигнала
- •8.2. Реализация спектрального анализа с использованием бпф
- •8.3. Синтез цифрового ких-фильтра
- •8.4. Реализация цифровой фильтрации
- •Список литературы
- •Содержание
- •197376, С.-Петербург, ул. Проф. Попова, 5
3.1.3. Эллиптические фильтры
Эллиптические фильтры характеризуются тем, что их амплитудная характеристика имеет равновеликие пульсации и в полосе пропускания, и в полосе непропускания. Эллиптические фильтры являются оптимальными с точки зрения минимальной ширины переходной полосы.
Квадрат амплитудной характеристики эллиптического фильтра нижних частот записывается в виде
![]() ,
,
где
![]() – рациональная функция Чебышева;L
– параметр, характеризующий
пульсации функции
– рациональная функция Чебышева;L
– параметр, характеризующий
пульсации функции
![]() .
.
3.1.4. Фильтры Бесселя
Фильтры Бесселя характеризуются максимально гладкой характеристикой групповой задержки в начале координат в s-плоскости. Переходная характеристика фильтров Бесселя имеет весьма малый выброс. Однако при дискретизации непрерывных фильтров Бесселя методами, рассмотренными далее, характерное для этих фильтров свойство максимальной гладкости характеристики групповой задержки не сохраняется.
Передаточная функция фильтров Бесселя записывается в виде
![]()
где B0
(S) – функция Бесселя
n-го порядка; d0
– константа нормирования;
![]()
Функции Бесселя удовлетворяют следующему рекуррентному соотношению:
![]()
с начальными условиями B0(S) = 1 и B0(S) = S + 1. Эти функции можно представить в виде
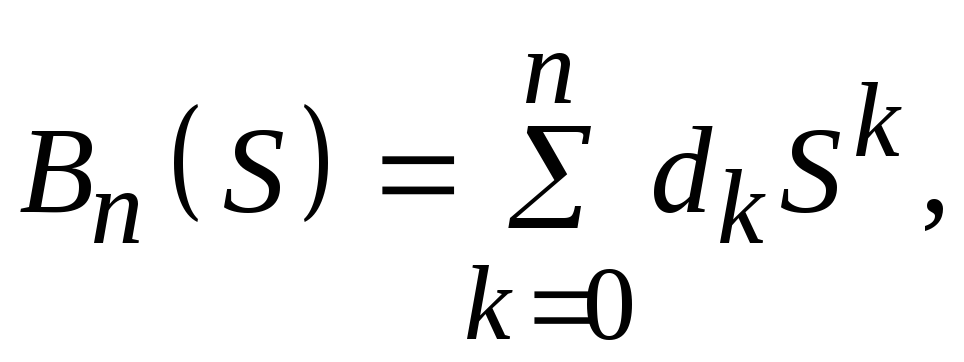
где
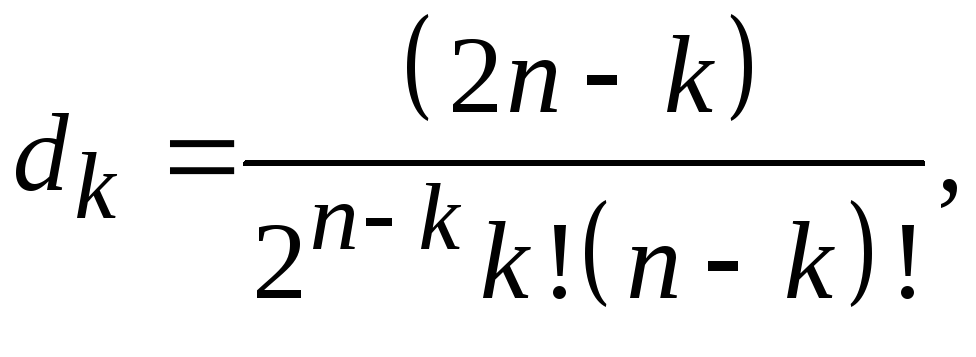 k = 1, 2, ...,n.
k = 1, 2, ...,n.
Фильтры Бесселя имеют только полюсы, которые расположены на окружности с центром на действительной положительной полуоси s-плоскости.
3.2. Методы дискретизации аналогового фильтра
Предположим, что передаточная функция аналогового фильтра (представляющая собой преобразование Лапласа от импульсной характеристики) равна:
 , (3.1)
, (3.1)
причем коэффициенты aiиbi(илиciиdi) известны.
Наиболее распространенными методами дискретизации аналогового фильтра с передаточной функцией (3.1) являются следующие:
метод отображения дифференциалов;
метод инвариантного преобразования импульсной характеристики;
метод билинейного преобразования;
метод согласованного z-преобразования.
Рассмотрим некоторые из них.
3.2.1. Метод инвариантного преобразования импульсной характеристики
Отличительной особенностью этого метода является то, что в качестве импульсной характеристики рассчитываемого цифрового фильтра используется дискретная импульсная характеристика соответствующего аналогового фильтра. В результате частотная характеристика цифрового фильтра образуется наложением частотной характеристики дискретизуемого аналогового фильтра.
Разложим выражение (3.1) на простые дроби:
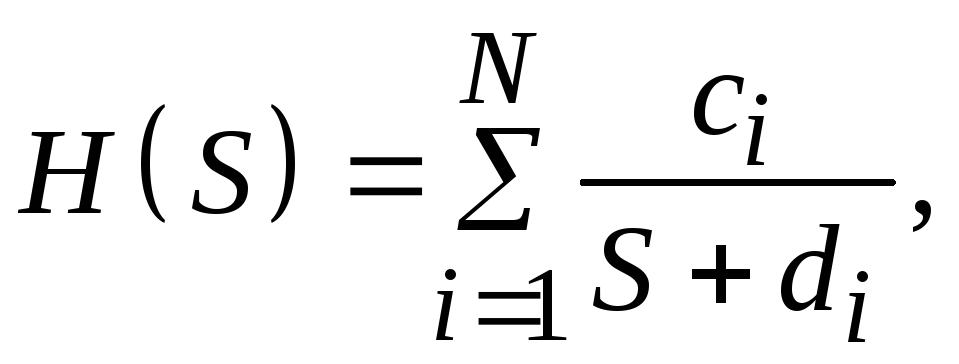
где ![]() ,
причем каждый коэффициентdi
определяет положение i-го
полюса. При записи разложения (3.1)
предполагалось, что порядок числителя
M меньше порядка
знаменателя N и все
полюсы H(S)
простые. Импульсная характеристика
h(t)
аналогового фильтра с передаточной
функцией вида (3.1) описывается соотношением
,
причем каждый коэффициентdi
определяет положение i-го
полюса. При записи разложения (3.1)
предполагалось, что порядок числителя
M меньше порядка
знаменателя N и все
полюсы H(S)
простые. Импульсная характеристика
h(t)
аналогового фильтра с передаточной
функцией вида (3.1) описывается соотношением
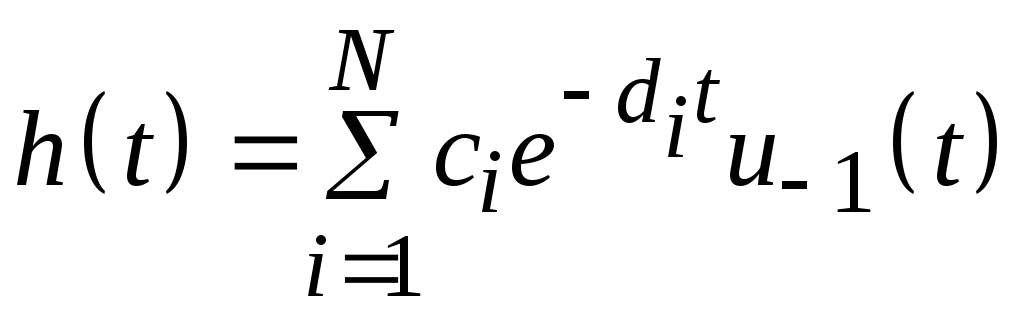 .
.
Дискретизуя ее, получим импульсную характеристику цифрового фильтра
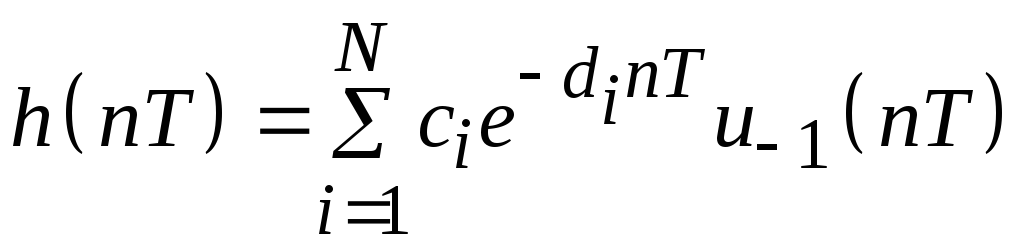 ,
,
где T – период дискретизации. Найдем ее z-преобразование:
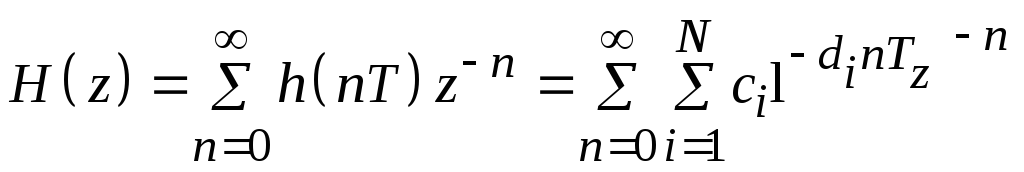 .
.
Изменив порядок суммирования и просуммировав по n, получим:
 (3.2)
(3.2)
Сравним формулы (3.1) и (3.2). Видно, что для простых полюсов переход от H(S) к H(z) осуществляется с помощью отображения, при котором используется замена
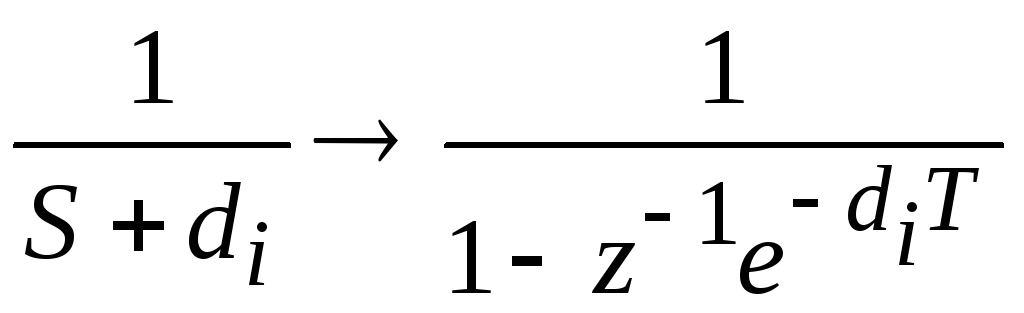 .
.
Если полюсы dj
комплексные, то остатки
cj в (3.1) также
будут комплексными. Функция h(t)
действительная, поэтому должны
существовать также комплексно сопряженные
полюс
![]() и
остаток
и
остаток![]() .
Просуммируем эти комплексно сопряженные
члены:
.
Просуммируем эти комплексно сопряженные
члены:
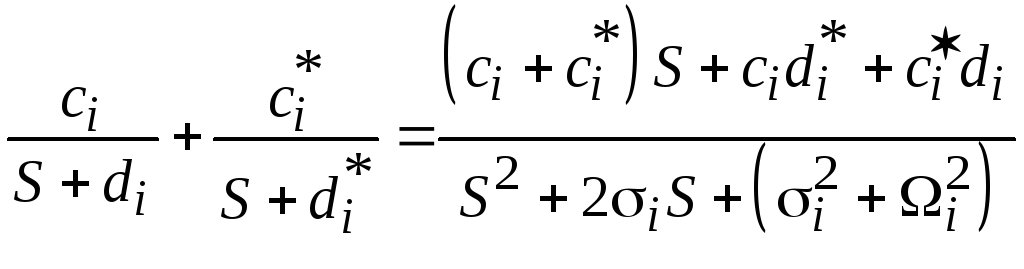 .
.
Примем di = si + Wi и ci = gi + jhi, тогда
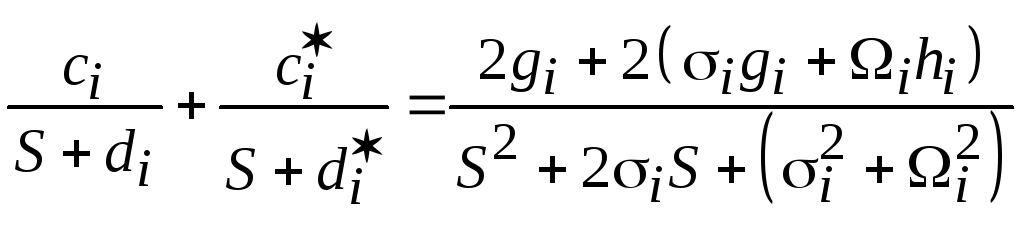 . (3.3)
. (3.3)
Использование отображающей замены применительно к каждому слагаемому в формуле (3.2) дает
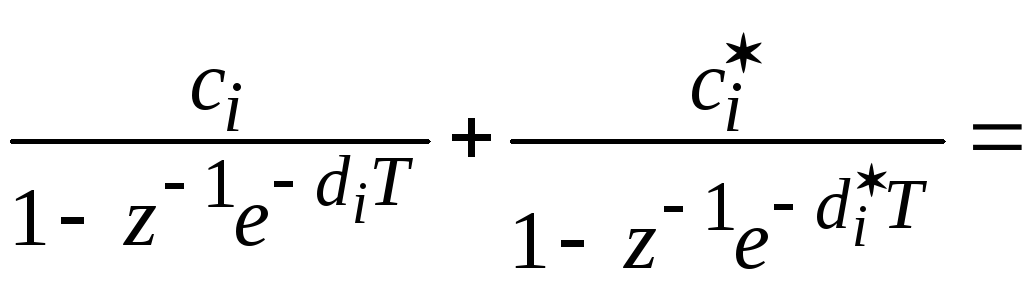
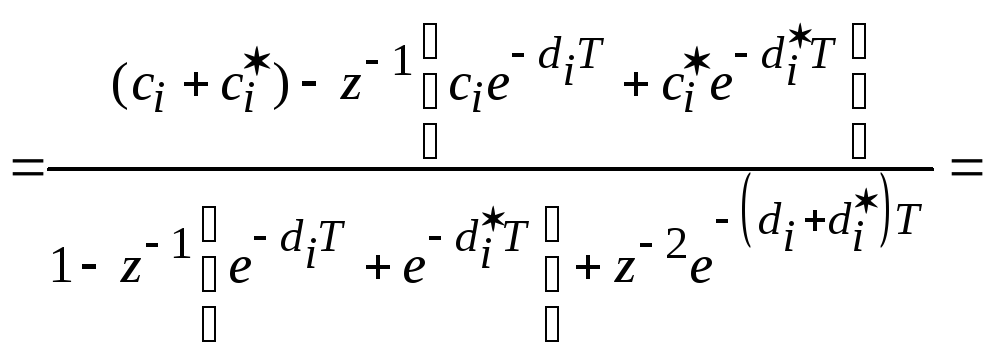
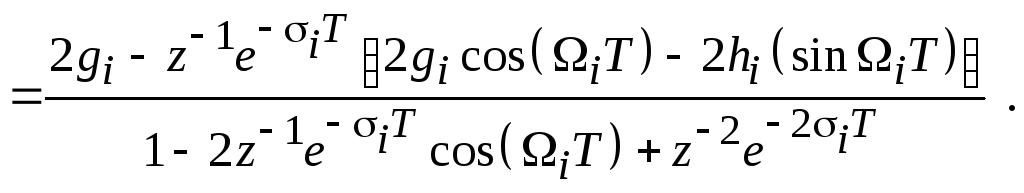 (3.4)
(3.4)
Из формул (3.3) и (3.4) получаем:
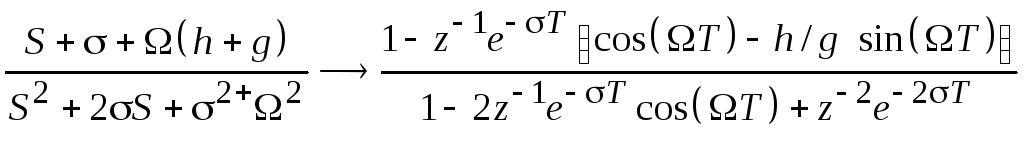
(индекс iздесь опущен, а числители разделены на 2g).
Частотная характеристика цифрового фильтра, рассчитываемого методом инвариантного преобразования импульсной характеристики, образуется путем наложения частотной характеристики дискретизуемого аналогового фильтра. Таким образом, можно записать:

где
![]() – угловая частота дискретизации
цифрового фильтра. На рис. 3.2
показано соответствующее инвариантному
преобразованию импульсной характеристики
отображение из s-плоскости
в z-плоскость. Каждая
горизонтальная полоса шириной
– угловая частота дискретизации
цифрового фильтра. На рис. 3.2
показано соответствующее инвариантному
преобразованию импульсной характеристики
отображение из s-плоскости
в z-плоскость. Каждая
горизонтальная полоса шириной
![]() изs-плоскости
отображается на
z-плоскость.
Поэтому все смежные полосы из s-плоскости
будут при отображении накладываться
друг на друга в z-плоскости.
изs-плоскости
отображается на
z-плоскость.
Поэтому все смежные полосы из s-плоскости
будут при отображении накладываться
друг на друга в z-плоскости.
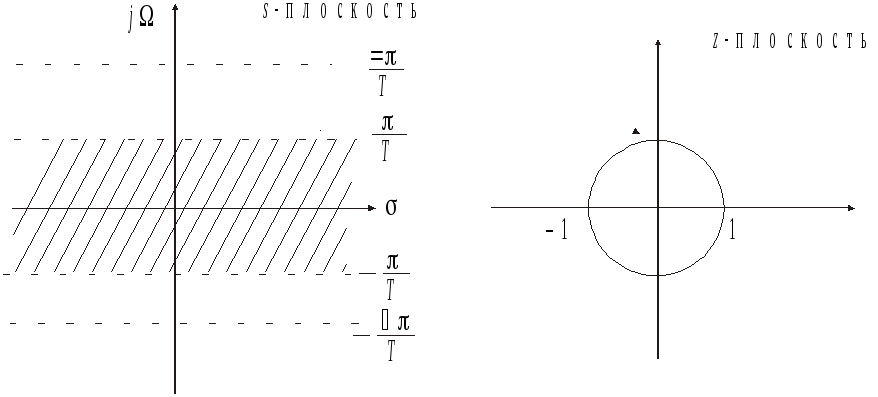
Рис. 3.2
Значит, для того чтобы частотные
характеристики исходного аналогового
фильтра и рассчитываемого методом
инвариантного преобразования импульсной
характеристики цифрового фильтра
соответствовали друг другу, необходимо,
чтобы полоса пропускания аналогового
фильтра находилась в пределах диапазона
![]() .
.
Для выполнения этого условия необходимо до начала преобразования вводить дополнительный фильтр нижних частот, гарантирующий соответствующее ограничение полосы пропускания аналогового фильтра.
Метод инвариантного преобразования импульсной характеристики дает хорошие результаты для баттервортовских, бесселевых или чебышевских фильтров нижних частот и полосовых фильтров. Достоинство этого метода заключается в сохранении в цифровом фильтре таких же фазовой характеристики и характеристики затухания, как и у исходного аналогового фильтра.
