1. Нахождение числовых характеристик выборки.

• Выборочная средняя

= 1.3247

• Выборочная дисперсия – характеризует отклонение чисел из выборки от среднего.

= 20.6864

• Исправленная выборочная дисперсия – более точная характеристика отклонения

= 20.8342

• Среднеквадратическое отклонение

= 4.5482

• Исправленное среднеквадратическое отклонение

= 4.5644

• Выборочные начальные моменты порядка 2,3,4

= 22.4413

= 107.4486

= 1741.7

• Выборочные центральные моменты порядка 3,4

= 22.9129

= 1399.4

• Выборочный коэффициент асимметрии – характеризует симмеирию графика распределения.

= 0.2435

• Выборочный коэффициент эксцесса – характеризует форму графика распределения

= 0.2701

• Мода – наиболее вероятное значение случайной веичины.

M_o = 2,24

• Медиана – делит область случайных чисел на два интервала, вероятность попадания в каждый из которых равна 0.5.

M_e =1,3542

3. Графическое представление выборки.

Таблица частот группировки выборки

4.Статистическое оценивание параметров.

Получив числовые характеристики из нашей выборки, мы должны оценить, подходят ли они для описания реальной случайной величины, выборку из значений которой мы по предположению взяли.

Получение оценок параметров методом моментов.

Приравняем выборочные и теоретические моменты для получения оценки.

Начальный момент порядка 1: Mx

Выборочный начальный момент порядка 1: x_ср

Mx  x_ср

a  x_ср

â  x_ср – оценка мат.ожидания

Центральный момент порядка 2: Dx

Выборочный центральный момент порядка 2: S²

Dx  S²

²  S²

²  S² – оценка дисперсии

Получение оценок параметров методом максимального правдоподобия

Найдем оценку параметров a , σ нормального распределения N(a, σ)

Необходимо найти максимум функции L(x) где х=(х₁, х₂…х_n ), n – объем выборки.

Решаем систему уравнений

подставим во 2-ое уравнение вместо а - и решаем его относительно σ

Убедимся, что точка

Составим матрицу вторых производных

и проверим отрицательную определенность матрицы А в точке

следовательно, функция L(х) имеет максимум, то есть получили оценки:

Исследование свойств полученных оценок

• Несмещенность

Оценка несмещенная, если Мθ = θ

Оценка мат.ожидания: â = x_ср

Проверка: Мâ = Мx_ср = Мξ = а. Несмещенная.

Оценка дисперсии: ² = S²

Проверка:

где

оценка смещена

оценка асимптотически несмещена

Вводят исправленную дисперсию, которая является несмещенной оценкой .

• Состоятельность

Оценка =g(x₁,…,x_n) состоятельная, если .

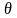Проверка оценки мат.ожидания:

Применим неравенство Чебышева

оценка параметра а состоятельная.

Проверка оценки дисперсии:

оценка S² параметра σ² состоятельная

• Эффективность

Оценка эффективна, если Dθ = 1/I ,где I – информационное кол-во Фишера.

Проверка оценки мат.ожидания:

оценка мат.ожидания эффективна

Проверка оценки дисперсии:

Оценка дисперсии ² = S² смещена, поэтому неэффективна. Проверим несмещенную оценку ² = S²_исп

- верно оценка эффективна

• Оптимальность

Если оценка эффективна, то она – оптимальна.

Оценка мат.ожидания оптимальна.

Оценка дисперсии S² неоптимальна.

Оценка дисперсии S²_исп оптимальна.

• Нормальность(принадлежность нормальному закону)

Проверка оценки мат.ожидания:

Оценка мат.ожидания нормальна

Проверка оценки дисперсии:

Используем ЦПТ.

Если случайные величины ₁, ₂, …,_n независимы, одинаково распределены и имеют конечные мат.ожидания и дисперсии, то

при n → ∞

где Ф(х) – функция стандартного нормального распределения.