4. Линейные пространства, подпространства. Примеры. Свойства пространств. Линейная зависимость и независимость системы векторов. Базис пространства.

Пусть P – это некоторое поле. Пусть V – это некоторое множество, элементы которого будем называть векторами и обозначать латинскими буквами (a,b,c). Элементы поля P будем называть скалярами и обозначать латинскими буквами .

Пусть задана операция умножения скаляра на вектор: , P VV.

Множество B назовем векторным (линейным пространством над полем P, если: (две операции: сложение и умножение)

1. Во множестве V задана алгебраическая операция сложения, обладающая свойствами:

(V,+) – абелева группа

а) ( a, b, c  V) (a+b)+c=a+(b+c)

б) (   V) ( a V) +a=a=a+

в) ( a  V) ( -a  V) a+(-a)=(-a)+a=

г) ( a, b  V) a+b=b+a

2. Операция умножения скаляра на вектор обладает свойствами:

а) ( a  V) 1 a = a

б) ( a, b  V) (   P) (a+b)= a+b

в) ( a  V) ( ,   P) (+)a=a+a

г) ( a  V) ( ,   P) ()a=a

- является векторным пространством.

Примеры линейных пространств:

1)

2) Рассмотрим =0 аддитивную группу - нулевое пространство.

3) Арифметическое n-мерное пространство . Его элементы – вектора.

4) - это множество многочленов степени не выше n от одной переменной X. Является линейным пространством над любым числовым полем (Q, R, C).

5) Обозначим - это векторное пространство, где F – множество функций, непрерывных на отрезке [a,b].

Простейшие свойства линейных пространств:

1. Так как (V,+) – абелева группа, то пространство, относительно сложения обладает всеми свойствами группы.

1) Наличие ! нулевого вектора.

2) Для каждого вектора из V существует противоположный вектор.

3) Сложение векторов коммутативно, ассоциативно и т.д.

4) Можно определить операцию вычитания векторов (( a, b  V) a-b= a +(-b))

5) Справедлив закон сокращения: ( a, b, c  V) a+b=a+c b=c

6) ( a, b  V) a + b = 0  a = -b  b = -a

2. ( a  L) ( k  P) ka =   k = 0  a = 

3. ( a  L) – a = - 1  a

4. ( a  L) ( k  P) (– k)a = - ka

5. ( a, b  L) ( k  P) k (a-b) = ka - kb

6. ( a  L) (  P)

Линейная зависимость и независимость векторов.

Линейной комбинацией нескольких векторов ( ) называется любой вектор вида: , - любые скаляры из P.

Вектор линейно выражается через .

Система векторов называется линейно зависимой, если существуют такие числа , одновременно, что линейная комбинация равна нулевому вектору .

Система векторов называется линейно независимой, если из того, что , следует, что все =0.

Свойства ЛЗ:

1. Система, состоящая из одного вектора линейно зависима в том и только том случае, когда этот вектор нулевой.

2. Критерий ЛЗ: Система состоящая более чем из одного вектора ЛЗ тогда и только тогда, когда какой-нибудь из этих векторов линейно выражается через остальные.

3. Система, содержащая нулевой вектор, всегда линейно зависима.

4. Если часть системы ЛЗ, то и вся система ЛЗ. Доказательство: Пусть часть системы является линейно зависимой. Для определенности обозначим первые k - векторов системы ЛЗ 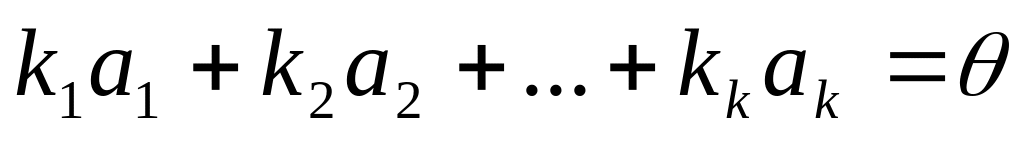. . 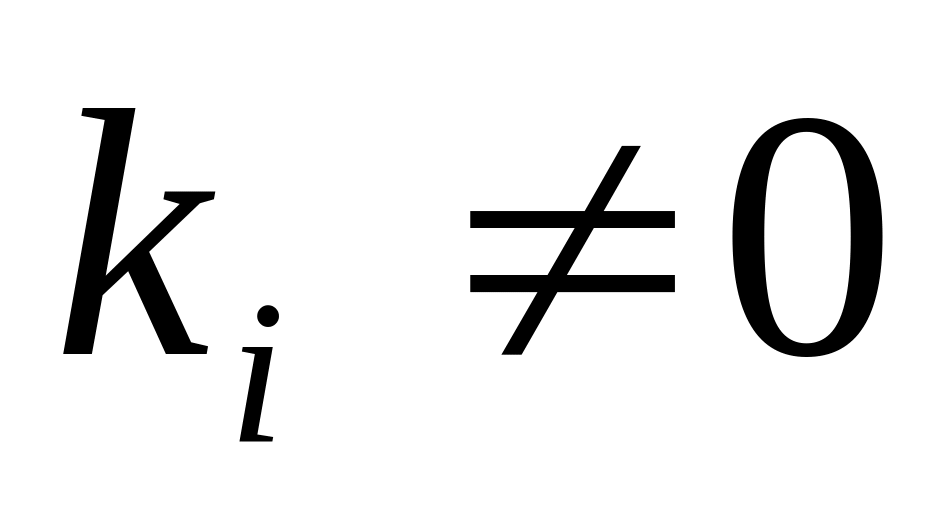Добавим к этой системе p – вектор 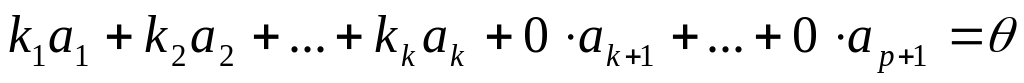, след-но, вся система является ЛЗ по определению.

5. Если система ЛНЗ, но при добавлении к ней еще одного вектора становится ЛЗ, то вектор линейно выражается через вектора .

П усть 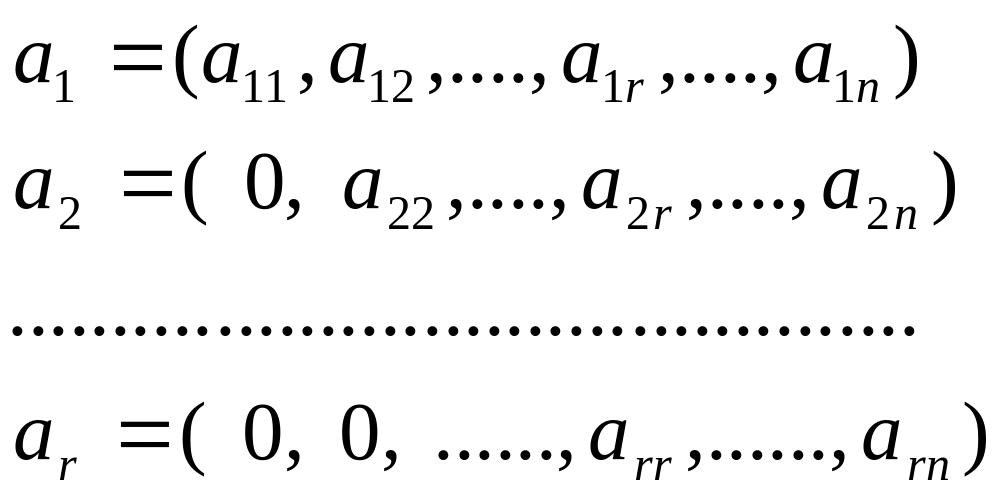. Систему, у которой все координаты ниже выделенной диагонали = 0 назовем лестничной.

6. Лестничная система векторов ЛНЗ.

Основная теорема ЛЗ. Пусть даны 2 системы векторов: и , . Тогда, если каждый вектор 1 системы линейно выражается через вектора 2 системы, то 1-я система – ЛЗ. Следствие 1. Если система векторов ЛНЗ и каждый вектор системы линейно выражается через систему , то . Следствие 2. В пространстве любая система, состоящая более чем из n-векторов ЛЗ.

Пример: В пространстве , 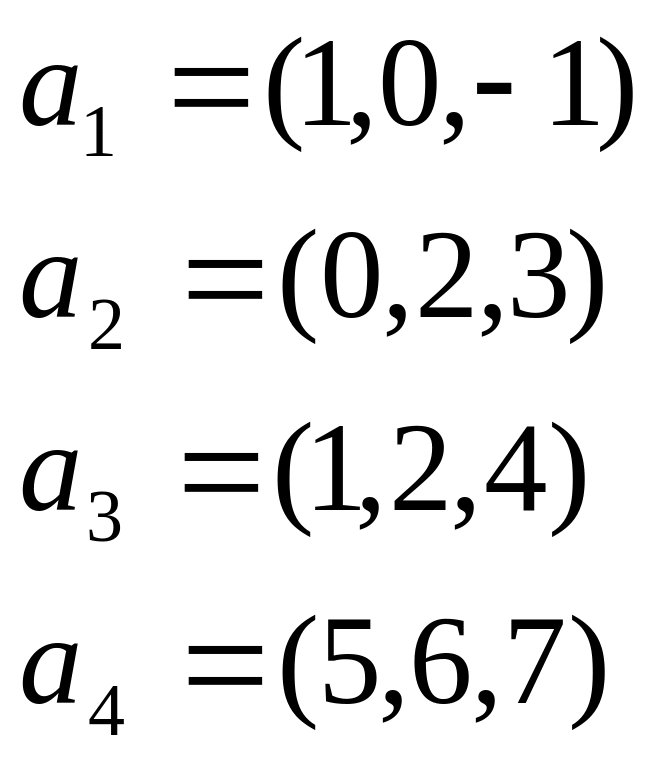ЛЗ, так как число векторов больше 3 (по 2 следствию).

Две системы векторов: (1) и (2) линейного пространства называются эквивалентными, если каждый вектор любой системы можно представить в виде линейной комбинации векторов другой системы (1) эквивал (2).

Базис и ранг системы векторов.

Пусть - некоторая система векторов. Выделим в этой системе подсистему, через которую будет выражаться любой вектор из этой системы.

Такая подсистема называется системой образующих для системы 1. Если подсистема образующих будет ЛНЗ, то система называется системой ЛНЗ образующих.

Подсистема системы 1 называется max линейно независимой, если она обладает следующими свойствами:

1. Подсистема ЛНЗ;

2. Приписывание к ней любого вектора системы делает ее ЛЗ.

Очевидно, что max ЛНЗ та подсистема, у которой число векторов max.

Базисом системы векторов называется любая ее подсистема, обладающая свойствами:

1. Подсистема ЛНЗ;

2. Любой вектор из системы натянут на эту подсистему, то есть линейно выражается через эту подсистему;

Базисом системы векторов называется ЛНЗ система образующих.

Базисом системы векторов называется любая ее max ЛНЗ подсистема.

Теорема (о существовании базиса): Любая конечная система из не равных 0 векторов имеет базис. Любые 2 базиса содержат одно и тоже число векторов.

Любая ЛНЗ подсистема данной системы является базисом или может быть дополнена до базиса. Система, содержащая хотя бы один не равный 0 вектор, обладает базисом. Эквивалентные системы векторов имеют базисы с одинаковым количеством векторов.

Рангом системы векторов называется количество векторов в базисе. Sign rang (A), r(A). Если система состоит из 0 векторов, то ее считают = 0.

Эквивалентные системы имеют одинаковый ранг. При элементарных преобразованиях rang системы векторов сохраняется.

Конечномерные пространства. Базис и размерность.

Линейное пространство называется конечномерным, если существует такое натуральное число n, что каждая система, содержащая > n векторов является ЛЗ. ЛНЗ систему конечномерного пространства называется базисом, если всякий вектор из L линейно выражается через данную систему.

Число векторов базиса пространства называют размерностью этого пространства. Sign dim L=n.

Любые 2 различных базиса пространства содержат одинаковое число векторов.

Теорема (о разложении вектора по базису). Любой вектор в n-мерном пространстве можно представить в виде линейной комбинации векторов базиса, причем ! образом.

Пусть V над полем P – линейное пространство. L   V.

называется подпространством пространства V, если оно является пространством относительно тех же операций сложения векторов и умножения скаляра на вектор, что и в пространстве V.

Критерий: Для того, чтобы являлось подпространством пространства V , чтобы выполнялись следующие 2 условия: 1. ( a, b  L) a + b  L, 2. ( a  L) (   P)  a  L.

Линейная оболочка линейного пространства V является его подпространством.

Пересечение подпространств пространства V является его подпространством.

Суммой 2-х подпространств H и T называется множество: .

Сумма подпространств пространства V, является его подпространством.

Сумма 2-х подпространств H и T является прямой в том и только том случае, если ( a  H+T) имеется единственное представление в виде: .