
- •Системы линейных уравнений. Разрешимость систем линейных уравнений (теорема Кронекера-Капелли).Методы решения.
- •Основные алгебраические структуры: группы, кольца , поля. Основные свойства. Примеры.
- •1. Гомоморфный образ группы также является группой относительно своей операции.
- •2. Пусть f: g1®g2 – гомоморфизм групп. Тогда
- •Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).
- •Определители и их свойства. Основные методы вычисления определителей.
- •Линейные пространства, подпространства. Примеры. Свойства пространств. Линейная зависимость и независимость системы векторов. Базис пространства.
- •5. Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
- •6. Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями.
- •7. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.
- •8. Линии второго порядка, их канонические уравнения, фокусы, директрисы, асимптоты.
- •9. Прямая и плоскость в пространстве, их уравнения. Взаимное расположение прямых и плоскостей.
- •10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •11. Операции над векторами векторного пространства v3. Векторный метод в решении геометрических задач.
- •12. Предел непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
- •13. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости.
- •14. Определенный интеграл, его свойства. Основная формула интегрального исчисления.
- •15. Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница.
- •18. Производная функция комплексного переменного. Условия Коши-Римана. Аналитическая функция.
- •19. Степенные ряды в действительной и комплексной области. Радиус сходимости.
- •20. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.
- •21. Уравнения в частных производных. Основные задачи математической физики. Метод Фурье.
- •23. Множества и способы их задания. Отношения и отображения. Понятие о мощности. Счетные и континуальные множества.
- •Свойства счетных множеств
- •Графическое представление
- •5. Основные тождества алгебры множеств
- •Принципы математической индукции
- •Отображение отношения функции
- •24. Коды постоянной и переменной длины, примеры их использования. Принцип работы архиватора.
- •25. Задача потребительского выбора и ее решение.
- •26. Понятие эластичности, геометрический смысл. Свойства эластичности, эластичность элементарных функций.
- •27. Производственная функция. Закон убывающей эффективности.
- •28. Транспортная логистика. Транспортная система России, ее особенности и характеристики. Маршруты движения автотранспорта. Математические методы для организации материала потока.
- •29. Задачи линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •3) Двойственная задача.
- •30. Нелинейное программирование. Методы решения задач.
5. Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
Пусть дано 2 векторных
пространства
![]() и
и
![]() .
Линейное отображение :
.
Линейное отображение :
![]()
![]() -
называется гомоморфизмом векторного
пространства, если выполняются 2 условия:
-
называется гомоморфизмом векторного
пространства, если выполняются 2 условия:
( a, b ) (a+b)= (a)+ (b) - аддитивность.
( a V) ( P) (a)= (a) - однородность.
Линейное отображение векторного пространства в себя называется линейным оператором, то есть линейный оператор – это гомоморфизм векторного пространства в себя.
Свойства линейного оператора:
Т.к. линейный оператор – это гомоморфизм, то выполняются все свойства гомоморфизма (() = , (-а) = -(а), линейно зависимая система переходит в линейно зависимую систему, образ линейной комбинации является линейной комбинацией образов с теми же коэффициентами).
Частный случай линейного оператора:
1) пусть pV – векторное пространство и отображение : VV – задано по правилу: (х) = х. Данное отображение является линейным оператором. Этот оператор называют тождественным или единичным.
2) пусть pV – векторное пространство и - фиксированный элемент поля Р. Отображение : VV – задано по правилу: (х) = х. Данное отображение является линейным оператором. Этот оператор называют оператором гомотетией с коэффициентом . Оператор гомотетии с коэффициентом = 0 называется нулевым оператором. Оператор гомотетии коэффициентом = 1 – есть оператор тождественный или единичный.
3) пусть L1 и L2 – подпространства пространства V, причем V = L1 L2. (хV) (!lL1) (!uL2) х = l + u. Рассмотрим : VV, которое каждому вектору х ставит в соответствие его компоненту lL1: хlL1. По свойствам подпространств - линейный оператор и его называют оператором проектирования.
4) пусть RF – векторное пространство действительных функций одной переменной х, определенных и неограниченно дифференцируемых на множестве R. Оператор D: FF, ставящий в соответствие каждому элементу из F его производную, является линейным оператором. (fF) D(f) = f = df/dx; D(f + g) = D(f) + D(g); (f + g) = f +g; D(f) = D(f); f = f , где R. Этот оператор называется оператором дифференцирования.
Теорема: Пусть pV – векторное пространство и (е1, е2, …, еn) – базис. Возьмем произвольную систему векторов: а1, а2, …, аn пространства V. Тогда ! Линейное отображение (еi) = аi, i = 1, …, n.
Замечание: аналогичная теорема справедлива и для двух различных пространств.
Множество векторов
линейного пространства V,
которое под действием линейного оператора
переходит в ,
называется ядром
линейного оператора и обозначается
![]() :
:
![]() .
Т.е. ядро линейного оператора – это
полный прообраз нулевого вектора при
отображении
.
Т.е. ядро линейного оператора – это
полный прообраз нулевого вектора при
отображении
![]() .
Теорема:
Ядро ЛО
.
Теорема:
Ядро ЛО
![]() является подпространством этого
пространства.
является подпространством этого
пространства.
Размерность ядра
линейного оператора называется дефектом
линейного оператора и обозначается:
![]() .
.
Образом линейного
оператора называется множество всех
векторов образа линейного оператора:
![]() и обозначается:
и обозначается:
![]() .
.
Размерность образа
линейного оператора называется рангом
линейного оператора и обозначается:
![]() .
.
Теорема (о связи размерности векторного пространства с рангом и дефектом линейного оператора): Пусть - линейный оператор конечномерного векторного пространства V. Сумма ранга и дефекта ЛО = размерности пространства V.
Пусть
– конечномерное векторное пространство.
![]() –
базис пространства.
- линейный оператор пространства V.
–
базис пространства.
- линейный оператор пространства V.
Представим векторы
![]() в виде линейной комбинаций базиса
(1):
в виде линейной комбинаций базиса
(1):
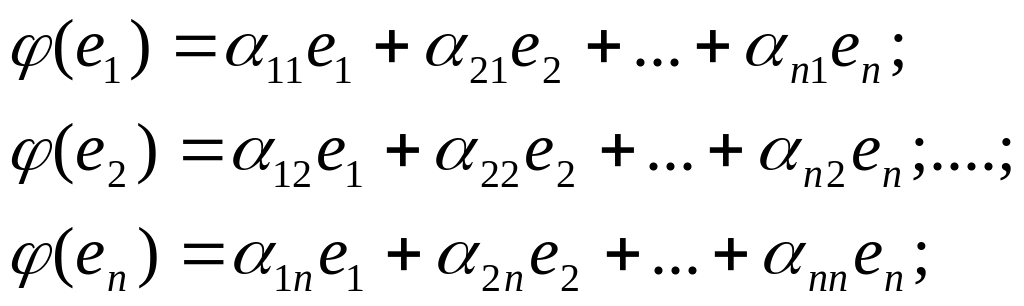
Матрица
![]() - это матрица линейного оператора
относительно базиса
.
- это матрица линейного оператора
относительно базиса
.
Теорема (связь м\у матрицей ЛО относительно различных базисов).
Пусть V- ненулевое конечномерное векторное пространство.
(1)
![]() (2).
(2).
![]() и
и
![]() .
.
T
– матрица перехода от (1) ко (2).
![]()
Пусть дан
- ЛО векторного пространства.
![]() и
и
![]() - это матрицы этого оператора, соответственно
относительно (1) и (2) базисов. Тогда
- это матрицы этого оператора, соответственно
относительно (1) и (2) базисов. Тогда
![]() .
.
Действия над линейными операторами:
1)
Суммой ЛО
и
будем называть отображение, определяемое
формулой:
![]()
![]() .
.
Теорема: сумма ЛО пространства V есть ЛО этого пространства.
Док-во:
1)
![]() - отображение.
- отображение.
![]()
![]() .
.
Док-во:
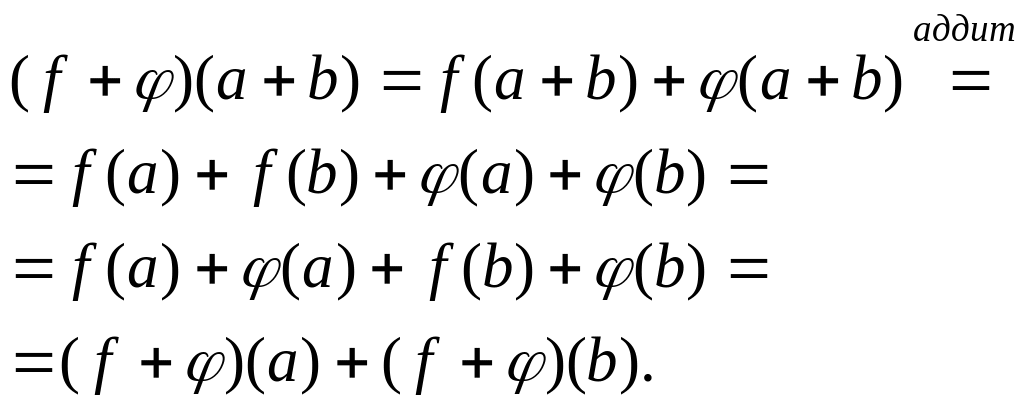
2)
![]()
![]() .
.
Док-во:
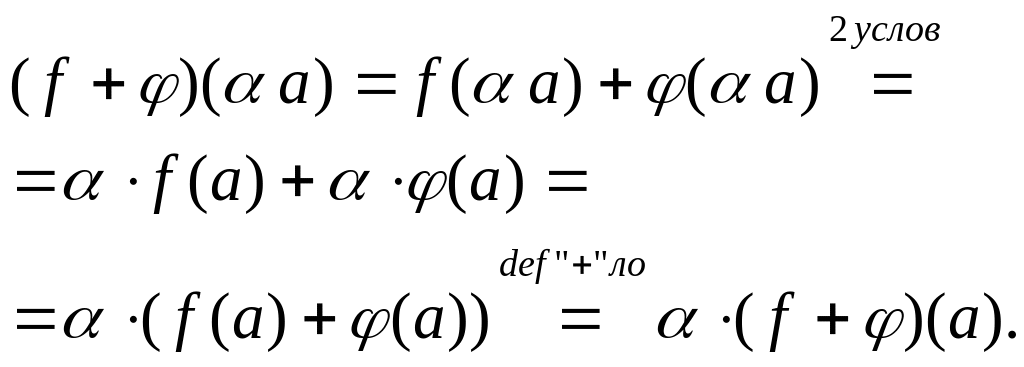
2)Если
- ЛО конечномерного векторного пространства
и
,
то
![]() будем называть отображение, определяемое
формулой:
будем называть отображение, определяемое
формулой:
![]() ().
().
3)
Пусть
и
- ЛО пространства V,
произведением ЛО
![]() называется отображение, ставящее в
соответствие элементу
называется отображение, ставящее в
соответствие элементу
![]() :
:
![]() .
.
![]() .
.
Оператор
- называется обратимым, если для него
![]() обратный ЛО.
обратный ЛО.
![]() .
.
![]() - тождественный оператор. Т.е., если
- тождественный оператор. Т.е., если
![]() - обратный к
,
то
- обратный к
.
Поэтому
и
взаимнообратные ЛО.
- обратный к
,
то
- обратный к
.
Поэтому
и
взаимнообратные ЛО.
Оператор пространства назовем невырожденным, если его дефект =0, в противном случае ЛО будем называть вырожденным.
Собственные векторы и собственные значения.
Ненулевой вектор
линейного
пространства
называется собственным вектором ЛО
,
если
![]() и
и
![]() .
Число
.
Число
![]() при этом называется собственным значением
вектора
относительно оператора
.
при этом называется собственным значением
вектора
относительно оператора
.
Пример: (х, у)(2х, 2у).
Свойства СВ и СЗ:
1)Собственны вектор ЛО имеет ! собственное значение относительно одного и того же ЛО.
Д-во:
(МоП) Пусть собственный вектор![]() имеет 2 собственных значения
имеет 2 собственных значения
![]() относительно оператора
.
относительно оператора
.
![]() ,
,
![]() ,
,
тогда в силу
однозначности оператора
:![]() .
.
![]() ,
,
![]()
![]() .
.
Наше предположение неверно, а верно то, что требовалось доказать.
2) Если – это ЛНЗ система собственных векторов ЛО с одним и тем же собственным значением , то любая линейная комбинация этих векторов, в которой хотя бы один коэффициент 0, является собственным вектором с тем же собственным значением .
Д-во:
Рассмотрим вектор
![]() ,
где
и
хотя бы один из
,
где
и
хотя бы один из
![]() .
.
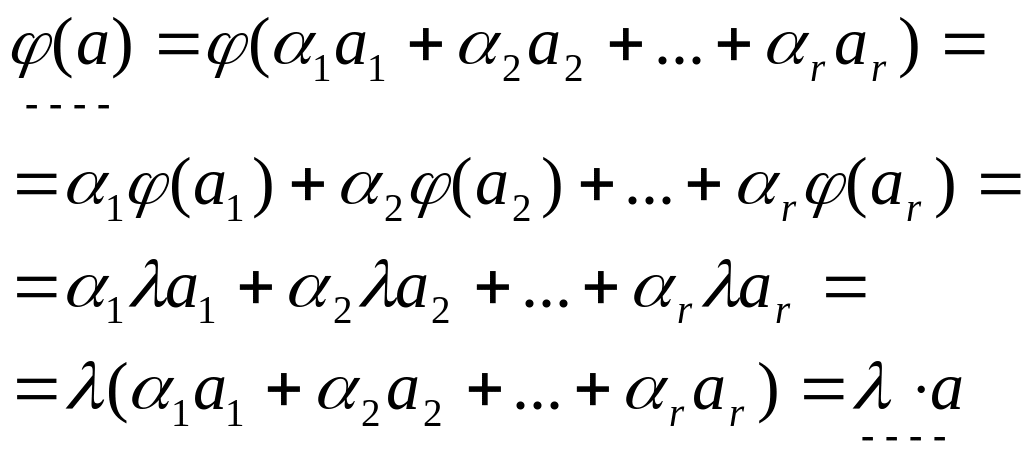
3) Все собственные векторы ЛО конечномерного пространства V, имеющие одно и то же собственное значение , вместе с образуют линейное пространство. Это подпространство называют собственным подпространством пространства V.
Теорема:
(Нахождение собственных векторов ЛО с
собственным значением
).
Пусть
-
ЛО и
- это собственное значение этого
оператора. Множество всех собственных
векторов с собственным значением
относительно
совпадает с множеством
![]() .
.
Теорема:
пусть
- ЛО векторного пространства Vn
и относительно базиса
.
Матрица этого оператора
и
число
является собственным значением ЛО
,
тогда определитель:
![]() (1).
(1).
Уравнение (1) с переменной называют характеристическим уравнением матрицы ЛО .
Т.о. задача по
отысканию собственных векторов ЛО
сводится к след. алгоритму: 1) зная
,
составить характеристическое уравнение
и решить его относительно переменной
.
2) найденные значения
![]() подставить в систему, полученную из
характеристического уравнения и
определить вектор
подставить в систему, полученную из
характеристического уравнения и
определить вектор
![]() Множество
собственных значений ЛО называют
спектром
ЛО
.
ЛО n-мерного
векторного пространства называют
оператором с простым спектром, если он
имеет n-различных
слбственных значений.
Множество
собственных значений ЛО называют
спектром
ЛО
.
ЛО n-мерного
векторного пространства называют
оператором с простым спектром, если он
имеет n-различных
слбственных значений.
Теорема: Если квадратные матрицы А и В подобны, то их характеристические уравнения совпадают.
