
- •Системы линейных уравнений. Разрешимость систем линейных уравнений (теорема Кронекера-Капелли).Методы решения.
- •Основные алгебраические структуры: группы, кольца , поля. Основные свойства. Примеры.
- •1. Гомоморфный образ группы также является группой относительно своей операции.
- •2. Пусть f: g1®g2 – гомоморфизм групп. Тогда
- •Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).
- •Определители и их свойства. Основные методы вычисления определителей.
- •Линейные пространства, подпространства. Примеры. Свойства пространств. Линейная зависимость и независимость системы векторов. Базис пространства.
- •5. Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
- •6. Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями.
- •7. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.
- •8. Линии второго порядка, их канонические уравнения, фокусы, директрисы, асимптоты.
- •9. Прямая и плоскость в пространстве, их уравнения. Взаимное расположение прямых и плоскостей.
- •10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •11. Операции над векторами векторного пространства v3. Векторный метод в решении геометрических задач.
- •12. Предел непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
- •13. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости.
- •14. Определенный интеграл, его свойства. Основная формула интегрального исчисления.
- •15. Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница.
- •18. Производная функция комплексного переменного. Условия Коши-Римана. Аналитическая функция.
- •19. Степенные ряды в действительной и комплексной области. Радиус сходимости.
- •20. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.
- •21. Уравнения в частных производных. Основные задачи математической физики. Метод Фурье.
- •23. Множества и способы их задания. Отношения и отображения. Понятие о мощности. Счетные и континуальные множества.
- •Свойства счетных множеств
- •Графическое представление
- •5. Основные тождества алгебры множеств
- •Принципы математической индукции
- •Отображение отношения функции
- •24. Коды постоянной и переменной длины, примеры их использования. Принцип работы архиватора.
- •25. Задача потребительского выбора и ее решение.
- •26. Понятие эластичности, геометрический смысл. Свойства эластичности, эластичность элементарных функций.
- •27. Производственная функция. Закон убывающей эффективности.
- •28. Транспортная логистика. Транспортная система России, ее особенности и характеристики. Маршруты движения автотранспорта. Математические методы для организации материала потока.
- •29. Задачи линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •3) Двойственная задача.
- •30. Нелинейное программирование. Методы решения задач.
7. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.
Известно, что х2 + а = 0 – данное уравнение не имеет решений в R при а > 0, в частности неразрешимо уравнение х2 + 1 = 0. Можно построить такое расширение поля R, в котором содержится хотя бы 1 элемент, удовлетворяющий уравнению х2 + 1 = 0.
Б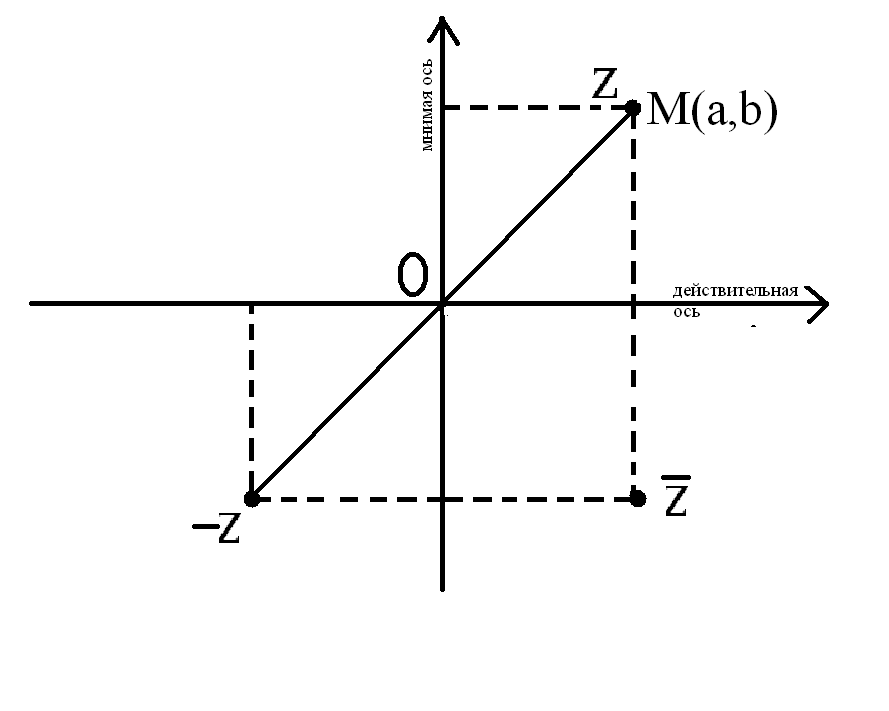 удем
называть полем
комплексных чисел
любое поле С, для которого выполняются
3 условия:
удем
называть полем
комплексных чисел
любое поле С, для которого выполняются
3 условия:
1) поле С является расширением поля R.
2) некоторый элемент поля С удовлетворяет уравнению х2 + 1 = 0, где 1 и 0 – нейтральные элементы поля относительно «» и «+».
3) всякое подполе поля С, удовлетворяющее условиям 1 и 2, совпадает с полем С.
Построим некоторое
поле комплексных чисел и убедимся, что
такие поля существуют.
![]() .
.
Введем операции
«+» и «»
на этом множестве следующим образом:
![]()
![]() .
Множество (С,+, )
– поле.
.
Множество (С,+, )
– поле.
Нейтральный элемент – это пара (0,0)=0 относительно сложения, относительно умножения 1=(1,0).
Пример:
![]() ,
,
![]() .
.
Обратный элемент
к паре
![]() :
:
![]() .
.
Назовем построенное нами поле, полем комплексных чисел, а его элементы комплексными числами.
Введем обозначения:
![]() ,
,
![]() ,
,
![]() .
.
![]() -
называют мнимой единицей.
-
называют мнимой единицей.
![]() .
.
![]() -
алгебраическая форма комплексного
числа.
-
алгебраическая форма комплексного
числа.
- действительная часть комплексного числа.
![]() - мнимая часть.
- мнимая часть.
![]() .
.
![]() - действительная часть,
- действительная часть,
![]() - мнимая часть (
- мнимая часть (![]() – коэф мнимой части).
– коэф мнимой части).
Операции над комплексными числами в алгебраической форме:
1.
![]()
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
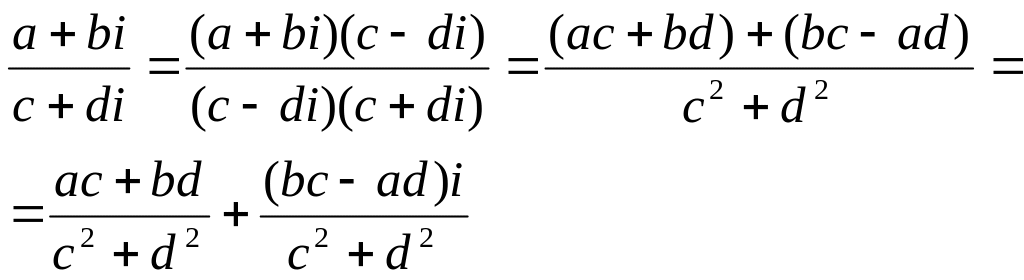
Пример:
![]()
Сопряженные числа.
![]() - сопряженное
комплексному числу
.
- сопряженное
комплексному числу
.
![]() .
.
Свойства сопряженных чисел:
1.
![]() .
.
2.
![]() .
.
3.![]() .
Доказательство: Пусть
.
Доказательство: Пусть
![]() ,
,
![]() .
.
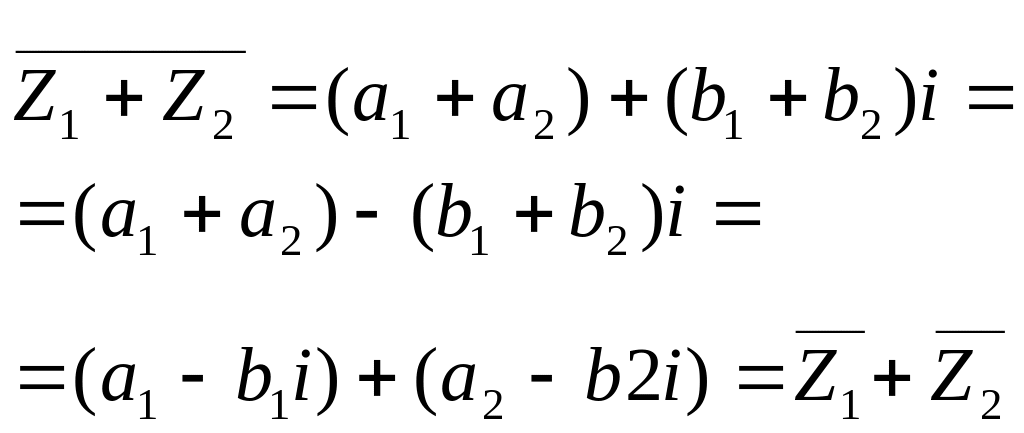
4.
![]() .
.
5.
![]() .
.
6.
 .
.
Число
![]() является противоположным к
является противоположным к
![]() ,
т.е.
,
т.е.
![]() .
.
Число
![]() (
(![]() )
называется обратным для
обозначается
)
называется обратным для
обозначается
![]() .
.
Геометрическая интерпретация комплексного числа.
Каждому числу
![]() поставим
в соответствие точку
поставим
в соответствие точку
![]() с абсциссой
и ординатой
и эта точка называется точкой, изображающей
число
.
с абсциссой
и ординатой
и эта точка называется точкой, изображающей
число
.
Также геометрической
формой комплексного числа
служит радиус-вектор
![]() .
.
Представление геометрически операции над комплексными числами.
Положение точки на плоскости может определяться заданием ее полярных координат: полярный радиус и полярный угол.
Такая система задания точки на плоскости получила название полярной системы координат.
Модулем комплексного
числа
![]() называется
называется
![]() .
.
![]() ,
,
![]() .
Геометрический смысл: Это расстояние
от точки О
до точки М
или длина вектора ОМ.
.
Геометрический смысл: Это расстояние
от точки О
до точки М
или длина вектора ОМ.
Для любых комплексных
чисел
и
![]() справедливы следующие свойства:
справедливы следующие свойства:
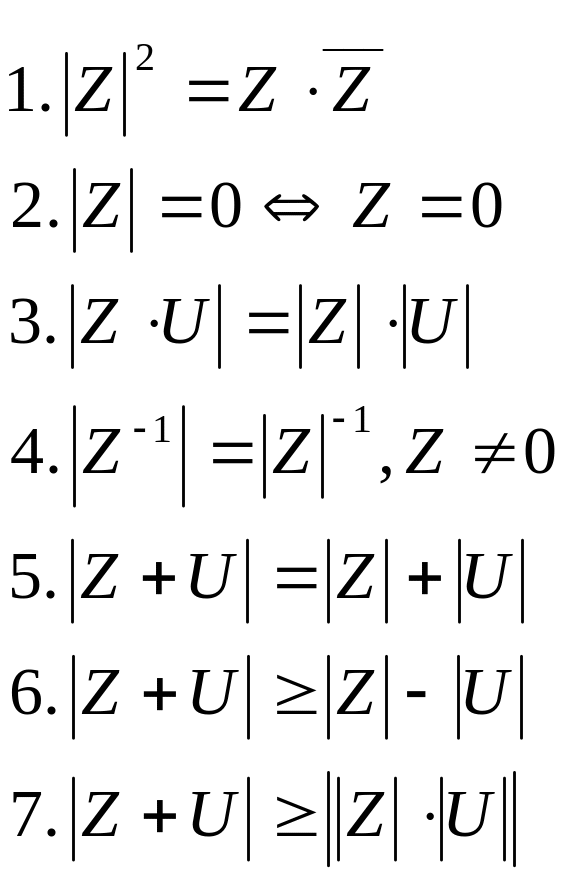
Аргументом
комплексного числа
называется
![]() число
,
такое, что
число
,
такое, что
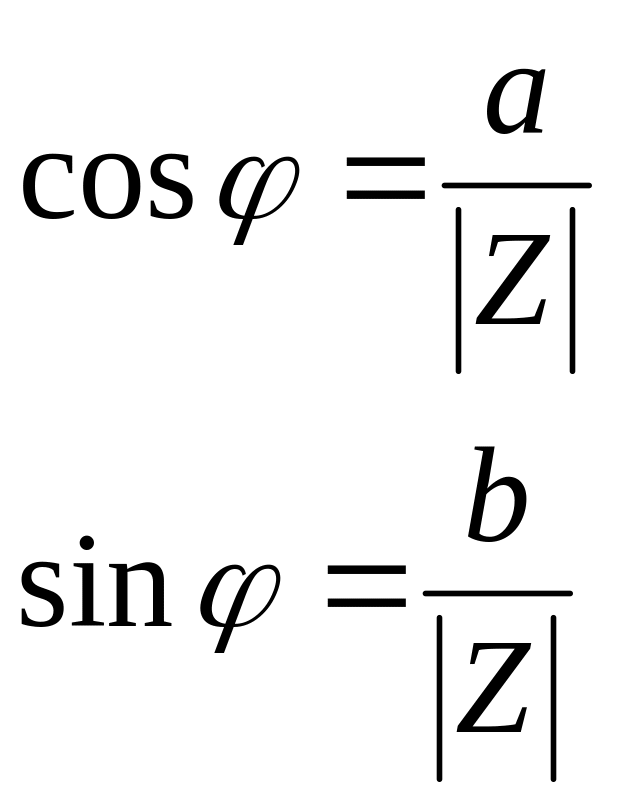
Угол
может принимать любые
значения, как положительные, так и
отрицательные, причем положительные
углы должны отсчитываться против часовой
стрелки. Однако, если углы отличаются
друг от друга на
![]() или число, кратное
,
то соответствующие им точки плоскости
совпадают. Т.о. аргумент комплексного
числа
имеет
или число, кратное
,
то соответствующие им точки плоскости
совпадают. Т.о. аргумент комплексного
числа
имеет
![]() много значений, отличающихся друг от
друга на целое кратные числа
.
много значений, отличающихся друг от
друга на целое кратные числа
.
Теорема (О представлении комплексного числа в тригонометрической форме).
Каждое комплексное
число
можно представить в виде:
![]() ,
где
,
где
![]() ,
,
![]() ,
,
- аргумент комплексного числа
.
Выражение комплексного числа
в данном виде называется тригонометрической
формой комплексного числа.
,
,
- аргумент комплексного числа
.
Выражение комплексного числа
в данном виде называется тригонометрической
формой комплексного числа.
Действия над комплексными числами в тригонометрической форме:
Теорема:
1. Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
2.
![]() .
.
Из теоремы можно привести равенство: |z1z2| = |z1||z2| = r1r2, arg(z1z2) = argz1 + argz2 и |z1/z2| = |z1|/|z2| = r1/r2, arg(z1/z2) = argz1 - argz2.
Степенью комплексного
числа
называется
![]() .
.
![]()
![]()
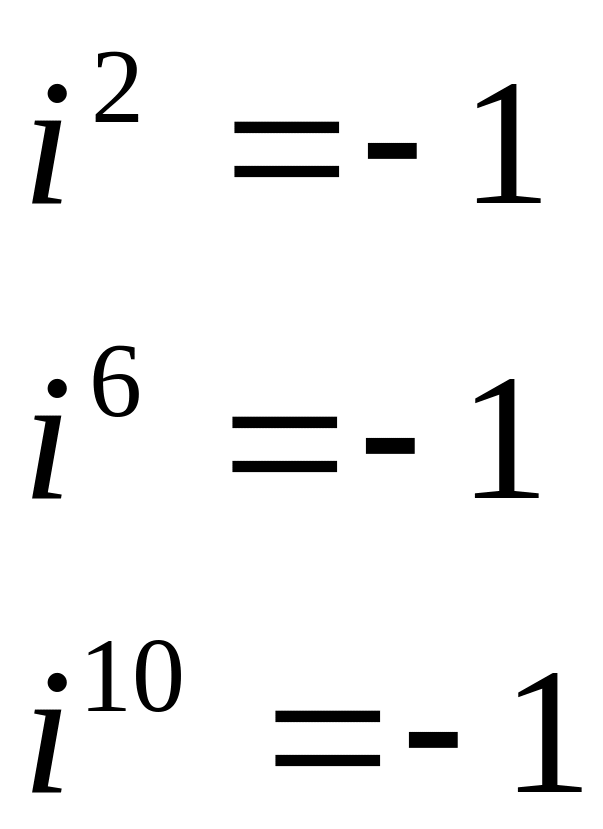
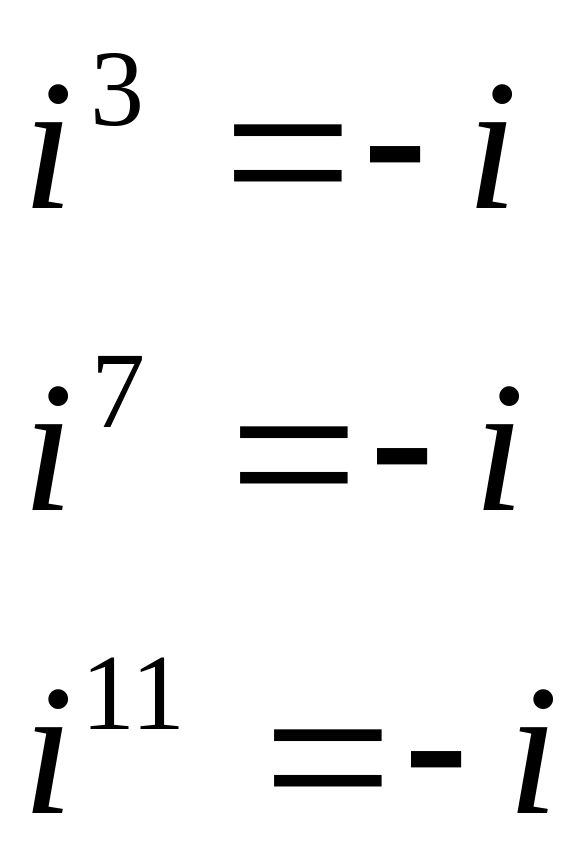
Пример:
![]()
Теорема (о степени комплексного числа в тригонометрической форме). При возведении комплексного числа в степень, модуль комплексного числа возводится в эту степень, а аргумент комплексного числа умножается на показатель степени.
![]() - 1-я формула Муавра.
- 1-я формула Муавра.
![]() - 2-я формула Муавра
(частный случай к первой формуле).
- 2-я формула Муавра
(частный случай к первой формуле).
При
 левая часть:
левая часть:
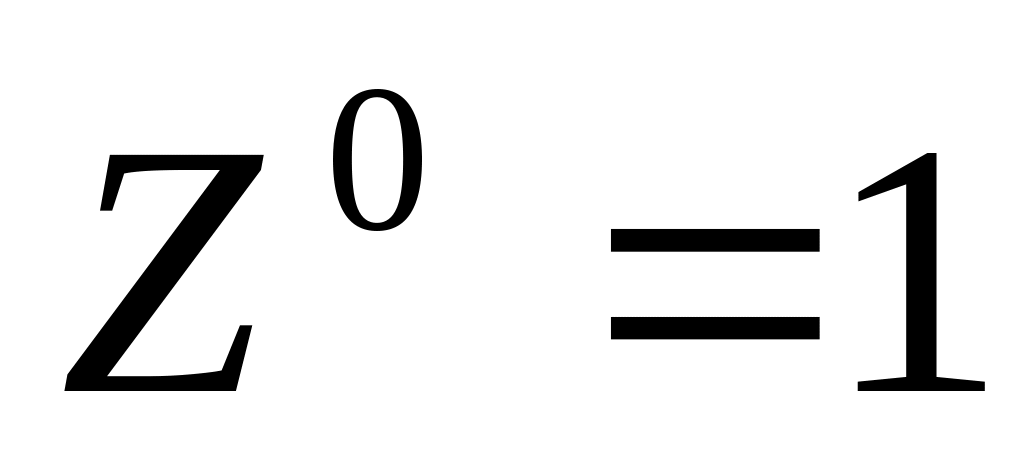 ,
правая часть:
,
правая часть:
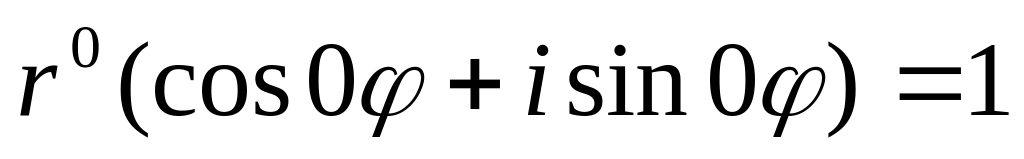 .
1=1
формула справедлива.
.
1=1
формула справедлива.При
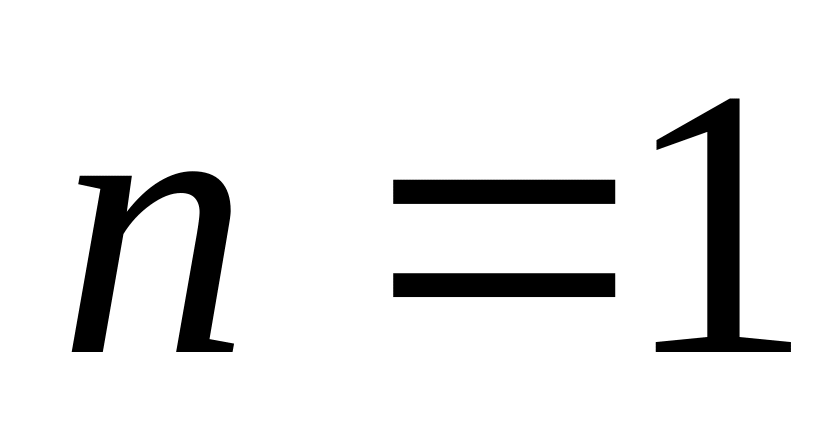 левая часть:
левая часть:
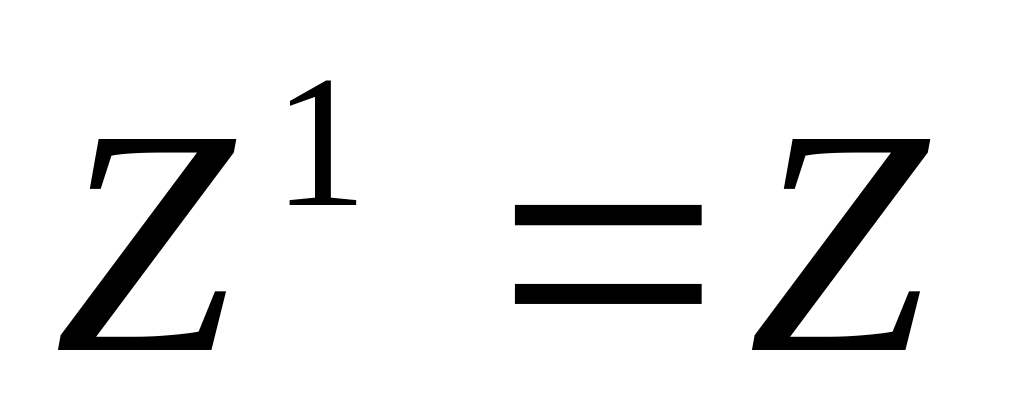 ,
правая часть:
,
правая часть:
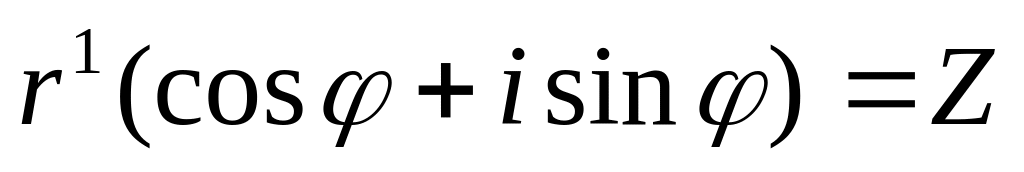 .
.
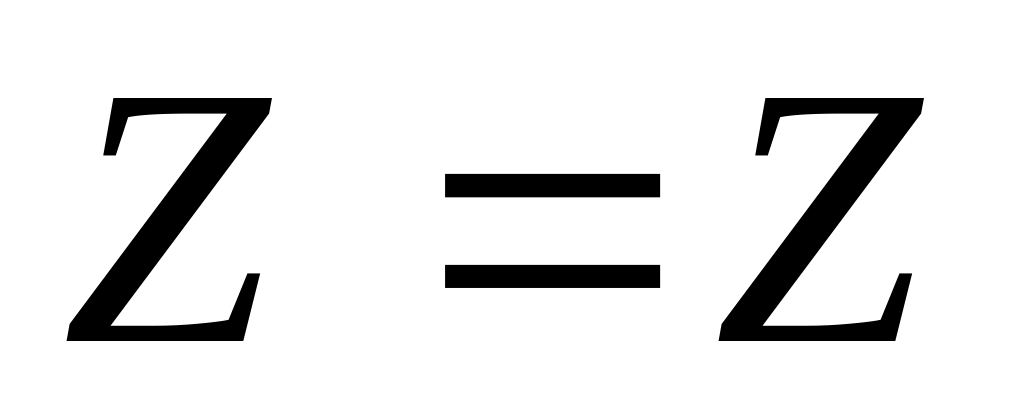 формула справедлива.
формула справедлива.(
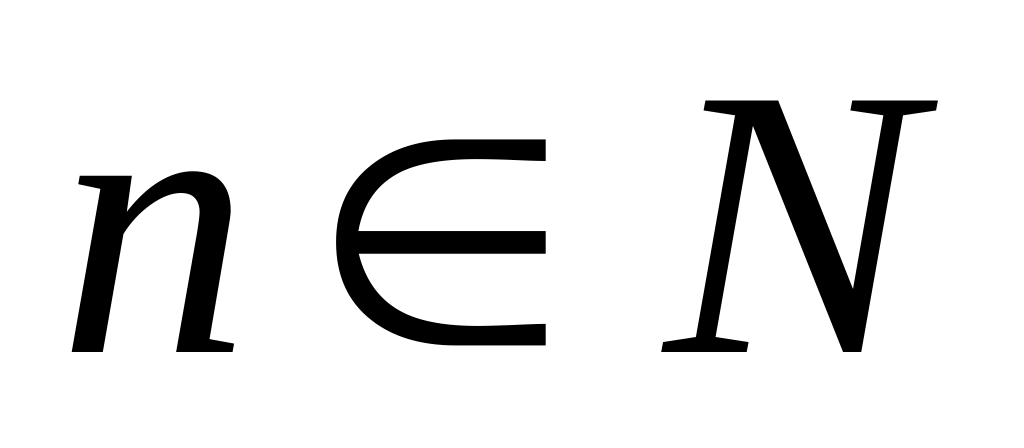 ).
Воспользуемся ММИ.
).
Воспользуемся ММИ.
Базис индукции.
(доказано, см. пункт 2)
Индукционный шаг: Пусть формула Муавра выполняется для
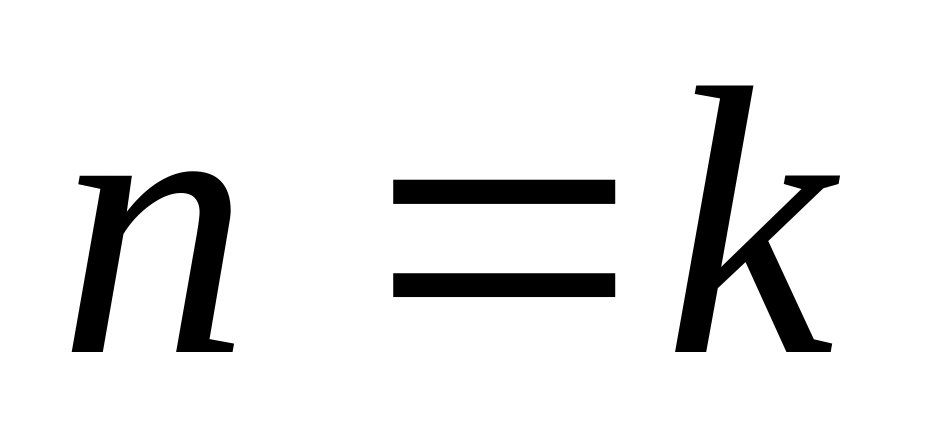 ,
,
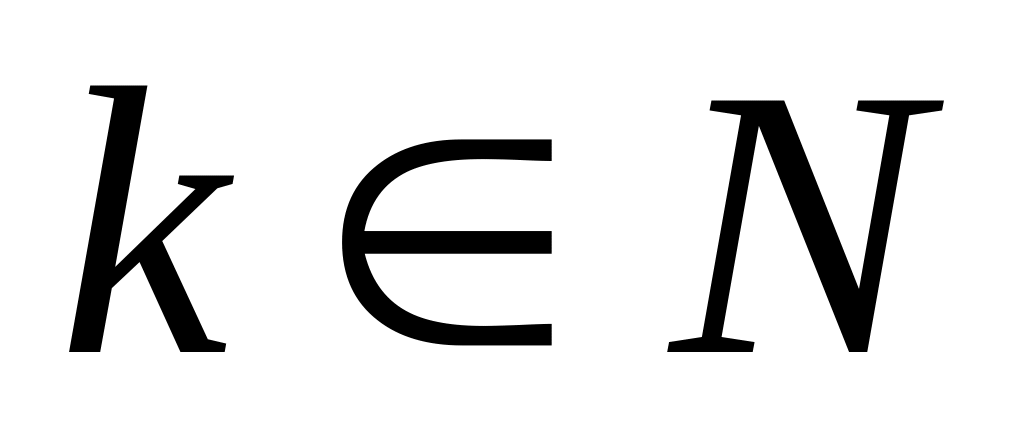
![]() .
Докажем, что она выполняется для
.
Докажем, что она выполняется для
![]()
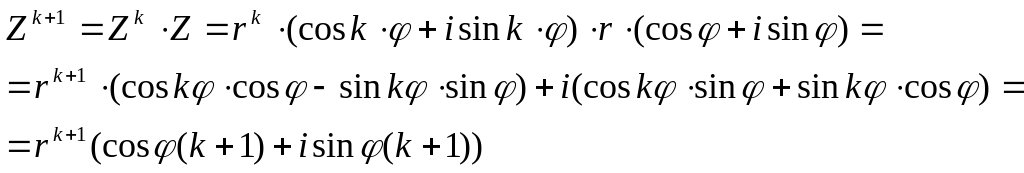
В правой части получили то, что требовалось доказать. Согласно ММИ данная формула верна ( ).
Рассмотрим
 .
.
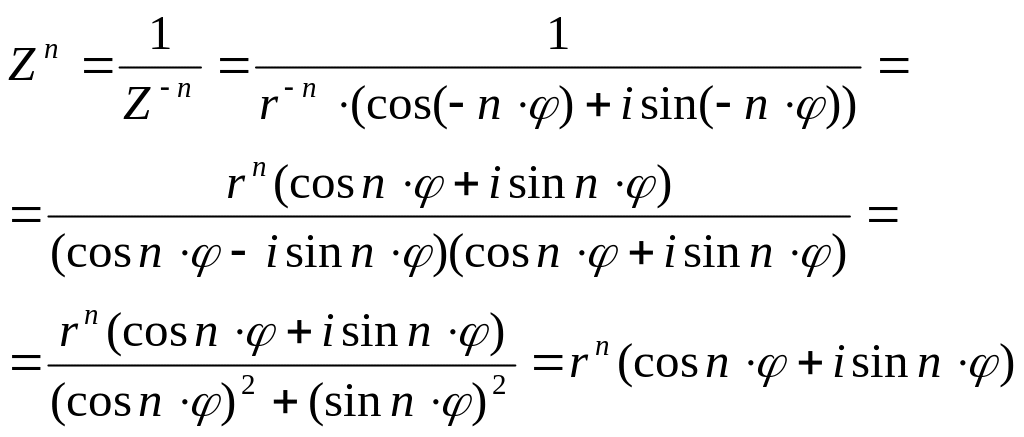
Из пунктов 1-4 формула
справедлива
![]()
Извлечение корней.
Комплексное число
называется корнем
-й
степени из комплексного числа
,
если
![]() ,
,
,
,
![]()
![]() .
.
Теорема
о корне
-й
степени из комплексного числа. Корень
-й
степени из комплексного числа
![]() имеет ровно
значений; если
задано в тригонометрической форме.
,
то всеми значениями корня
-й
степени
имеет ровно
значений; если
задано в тригонометрической форме.
,
то всеми значениями корня
-й
степени
![]() будут числа
будут числа
![]() ,
,
![]() ,
,
![]() - арифметический корень.
- арифметический корень.
Геометрическая интерпретация .
Пусть
,
![]() .
Корнем
-й
степени из 1 называется такое комплексное
число
.
Корнем
-й
степени из 1 называется такое комплексное
число
![]() ,
-я
степень которого = 1 (
,
-я
степень которого = 1 (![]() ).
).
Теорема:
Существует точно
-различных
корней
![]() и все они получаются по формуле:
и все они получаются по формуле:
![]() ,
.
,
.
Свойства корней :
Множество значений замкнуто относительно умножения и деления. Множество всех значений относительно операции умножения является группой.
Число , являющееся значением называется первообразным корнем , если его степени
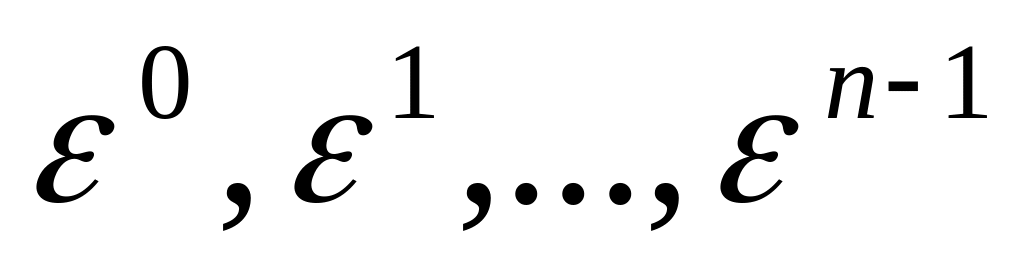 различны между собой. Это означает, что
они являются всеми значениями
.
различны между собой. Это означает, что
они являются всеми значениями
.
Пример:
