
- •1.Матрицы. Основные понятия. Прямоугольная таблица:
- •2.Действия над матрицами.
- •3.Обратная матрица. Пример.
- •7.Линейные операции над векторами.
- •8.Скалярное произведение векторов. Свойства.
- •12.Смешанное произведение векторов.
- •13.Функция. Основные понятия.
- •14.Пределы числовой последовательности.
- •17.Бесконечно малые функции и их свойства.
- •18. Бесконечно-большие функции и их свойства.
- •19. Основные теоремы о пределах.
- •20. Первый замечательный предел.
- •21. Второй замечательный предел.
- •23.Точки разрыва.
- •26.Таблица производных.
- •27.Основные прав ила дифференцирования.
- •Производная обратной функции
- •29.Дифференциал функции и его основные свойства.
- •30. Теоремы о дифференцируемых функциях.
- •31.Правило Лопиталя.
- •Существует конечный или бесконечный предел . Тогда: .
- •35.Прямая на плоскости. Способы задания.
- •36. Плоскость. Способы задания.
- •38.Взаимное расположение прямых.
- •39.Эллипс и его характеристики.
- •40. Гипербола.
- •44.Таблица интегралов.
- •48.Интегрирование по частям.
- •50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
- •Вычисление
- •58.Длина дуги.
44.Таблица интегралов.
|
|
|
|
|
|
|
|
|
10.
|
45.Метод подведения под знак дифференциала в неопределенном интеграле. Производная неопределенного интеграла равна подынтегральной функцией:
.Этот метод применяется для сведения интеграла к табличному путем замены какой нибудь части подинтегрального выражения его дифференциалом.
46.Метод подстановки.
Для упрощения подынтегральной функции
и, тем самым, для нахождения интеграла
![]() часто применяется так называемая
подстановка или замена переменных.
часто применяется так называемая
подстановка или замена переменных.
Если
обозначить
![]() и сделать соответствующие преобразования
в заданном подынтегральном выражении,
полученный интеграл при удачном выборе
функции
и сделать соответствующие преобразования
в заданном подынтегральном выражении,
полученный интеграл при удачном выборе
функции
![]() может оказаться более простым или даже
табличным.
может оказаться более простым или даже
табличным.
Для некоторых типов подынтегральных функций известны такие подстановки, которые приводят к цели. Ниже будут рассматриваться многие из них.
Например:
 .
Если применить замену
.
Если применить замену
 ;
;
 ,
то получим:
,
то получим:
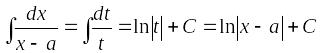 .
.
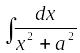 .
Применим замену
.
Применим замену
 ;
;
 .
В результате получим:
.
В результате получим:
 .
.
 Как
и в предыдущем случае, применим замену
;
.
В результате получим:
Как
и в предыдущем случае, применим замену
;
.
В результате получим:
 .
.
 .
Интегрирование этого выражения будет
проведено позднее при подробном
рассмотрении метода замены переменных.
.
Интегрирование этого выражения будет
проведено позднее при подробном
рассмотрении метода замены переменных.
Наряду с заменой переменных часто применяется метод разложения, который опирается на линейные свойства интегралов. Это можно проиллюстрировать следующим примером:
 .
.
47.Интеграл,
содержащий квадратный трехчлен.1. ,2.
,2. ;
3.
;
3. ;
4.
;
4. .
Для их нахождения нужно 1)выделить полный
квадрат двучлена, основание двучлена
обозначить через t,
а интегралы вида 1 и 3 –будут табличные,
а 2 и 4 – следует разбить на сумму двух
интегралов, один из которых будет
табличным, а другой берется подстановкой
или подведением под знак дифференциала.
.
Для их нахождения нужно 1)выделить полный
квадрат двучлена, основание двучлена
обозначить через t,
а интегралы вида 1 и 3 –будут табличные,
а 2 и 4 – следует разбить на сумму двух
интегралов, один из которых будет
табличным, а другой берется подстановкой
или подведением под знак дифференциала.
48.Интегрирование по частям.
Если
функции
![]() и
и
![]() дифференцируемы на множестве
и, кроме того, на этом множестве существует
интеграл
дифференцируемы на множестве
и, кроме того, на этом множестве существует
интеграл
![]() ,
то на нем существует и интеграл
,
то на нем существует и интеграл
![]() ,
причем
,
причем
![]() .
.
Действительно, если проинтегрировать формулу нахождения дифференциала произведения двух функций:
![]() ,
,
то можно получить следующее соотношение между первообразными от этих функций:
.
Такой
способ нахождения интеграла называется
интегрированием
по частям.
Этот способ
целесообразно применять, если интеграл,
стоящий в правой части проще исходного.
При использовании метода интегрирования
по частям задана левая часть равенства,
т.е. функция
и дифференциал
![]() .
Таким образом, выбор функций
и
неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла.
.
Таким образом, выбор функций
и
неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла.
Функции, интегрируемые по частям, можно схематично разделить на три группы.
1.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.
,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.

В случае если подынтегральная функция содержит в качестве множителя одну из перечисленных выше функций в степени , то операцию интегрирования по частям придется повторять раз.
2.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,
![]() ,
,
![]() ,
a
также, полином
,
a
также, полином
![]() й
степени
й
степени
![]() :
:
 .
.
Для вычисления интегралов второй группы нужно формулу интегрирования по частям применять раз, причем в качестве функции нужно брать многочлен соответствующей степени. После каждого интегрирования степень полинома будет понижаться на единицу.
3. Интегралы вида:
 ;
;
![]() ;
;
![]() .
.
Применение формулы интегрирования по частям может привести к ситуации, когда интеграл в правой части и интеграл в левой части равенства совпадают, т.е. получается равенство вида:
![]() ,
,
где
![]() исходный интеграл;
исходный интеграл;
![]() постоянная
постоянная
![]() .
.
В
этом случае применение метода
интегрирования по частям позволяет
получить уравнение первого порядка для
![]() ,
из решения которого находится исходный
интеграл
:
,
из решения которого находится исходный
интеграл
:
 .
.
Причем, метод интегрирования по частям может применяться многократно и любой из сомножителей можно всякий раз принимать за .
Большое количество интегралов, не входящих в эти три группы, у которых невозможно выделить общий признак для группировки, также вычисляются методом интегрирования по частям. К таким интегралам можно отнести:
![]() ,
,
![]() ,
,
 ,
,
 ,
,

49. Интегрирование
рациональных функций.
Из курса линейной алгебры известно, что
рациональной дробью называется выражение
вида
 ,
где
,
где
![]() и
и
![]() – многочлены степени
и
,
соответственно. Рациональная дробь
называется правильной при
– многочлены степени
и
,
соответственно. Рациональная дробь
называется правильной при
![]() .
В противном случае, когда
.
В противном случае, когда
![]() ,
рациональная дробь называется
неправильной. Деление числителя на
знаменатель позволяет от неправильной
дроби перейти к правильной.
,
рациональная дробь называется
неправильной. Деление числителя на
знаменатель позволяет от неправильной
дроби перейти к правильной.
При
интегрировании правильной рациональной
дроби производится разложение этой
дроби на простейшие, для чего предварительно
разлагается на элементарные множители
многочлен
.
Коэффициенты разложения определяются
методом неопределенных множителей.
Почленное интегрирование результатов
разложения сводится к вычислению
интегралов вида:
 и
и
 .
.
Интегралы вида вычисляются следующим образом:
 ;
; ;
;
Для вычисления интегралов вида применяются метод замены переменных и метод интегрирования по частям:

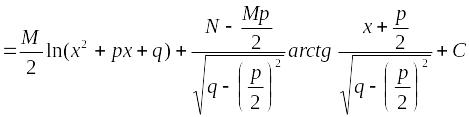 ;
;
Обозначим
 через
через
![]() ,
тогда
,
тогда
 .
Введем новую переменную
.
Введем новую переменную
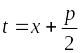 ,
тогда
,
тогда
![]() ,
,
 .
.


 ;
;
 .
.
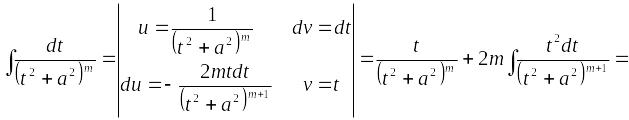

 .
.
Если
ввести обозначение
 ,
то полученное выражение можно переписать
в следующем виде:
,
то полученное выражение можно переписать
в следующем виде:

Таким
образом, происходит понижение порядка
вычисляемого интеграла, и вычисление
интеграла
![]() сводится к вычислению интеграла
сводится к вычислению интеграла
![]() .
.
Зная
с точностью до константы интеграл
 можно вычислить
можно вычислить
![]() :
:
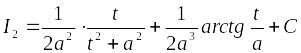 .
.
Используя
полученный результат, можно вычислить
![]() :
:

Таким образом, можно вычислить интеграл для любого натурального .

 ;
; ;
; ;
; ;
;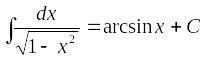 ;
;


