
- •1.Матрицы. Основные понятия. Прямоугольная таблица:
- •2.Действия над матрицами.
- •3.Обратная матрица. Пример.
- •7.Линейные операции над векторами.
- •8.Скалярное произведение векторов. Свойства.
- •12.Смешанное произведение векторов.
- •13.Функция. Основные понятия.
- •14.Пределы числовой последовательности.
- •17.Бесконечно малые функции и их свойства.
- •18. Бесконечно-большие функции и их свойства.
- •19. Основные теоремы о пределах.
- •20. Первый замечательный предел.
- •21. Второй замечательный предел.
- •23.Точки разрыва.
- •26.Таблица производных.
- •27.Основные прав ила дифференцирования.
- •Производная обратной функции
- •29.Дифференциал функции и его основные свойства.
- •30. Теоремы о дифференцируемых функциях.
- •31.Правило Лопиталя.
- •Существует конечный или бесконечный предел . Тогда: .
- •35.Прямая на плоскости. Способы задания.
- •36. Плоскость. Способы задания.
- •38.Взаимное расположение прямых.
- •39.Эллипс и его характеристики.
- •40. Гипербола.
- •44.Таблица интегралов.
- •48.Интегрирование по частям.
- •50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
- •Вычисление
- •58.Длина дуги.
50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
![]()
приводится
к интегралу от рациональной функции
при помощи подстановки
![]() ,
где
наибольшее
общее кратное показателей корней
,
где
наибольшее
общее кратное показателей корней
![]() .
.
Сходная подстановка рационализирует подынтегральную функцию и в более общем случае интегрирования выражений типа:
 .
.
В
этом случае также применяется подстановка
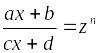 ,
где, как и в рассмотренном выше случае,
наибольшее
общее кратное показателей корней
,
где, как и в рассмотренном выше случае,
наибольшее
общее кратное показателей корней
![]() .
.
Вычисление
Интеграл
![]() сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
Если
 ,
то
,
то
 ;
;Если
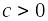 ,
то
,
то
 ;
;Если
 ,
,
то
![]() .
.
Здесь
![]() - новая переменная.
- новая переменная.
Интеграл
![]() находится подстановкой
находится подстановкой
![]() .
.
Интеграл
![]() находится подстановкой
находится подстановкой
![]() .
.
Интеграл
![]() находится подстановкой
находится подстановкой
 .
.
Пример:
Вычислить
 .
.
Применим
подстановку Эйлера
![]() .
Возводя это равенство почленно в квадрат,
получим
.
Возводя это равенство почленно в квадрат,
получим
![]() .
Дифференцируя обе части полученного
выражения, получим
.
Дифференцируя обе части полученного
выражения, получим
![]() .
Отсюда
.
Отсюда
![]() ,
или
,
или
 .
Таким образом,
.
Таким образом,
 .
Поскольку
.
Поскольку
![]() ,
то
,
то
![]() .
Следовательно,
.
.
Следовательно,
.
51-52. Интегрирование
тригонометрических функций.
Интеграл
![]() ,
где
,
где
![]() - рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки
- рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки
 .
При этом:
.
При этом:
 .
.
При
вычислении таких интегралов можно
использовать также и специальные
подстановки, а именно: в случае, когда
![]() ,
можно использовать подстановку
,
можно использовать подстановку
![]() .
.
В
случае неопределенного интеграла вида
![]() это соответствует нечетному значению
.
это соответствует нечетному значению
.
Если
![]() ,
можно
использовать подстановку
,
можно
использовать подстановку
![]() .
.
Если
![]() ,
то можно использовать подстановку
,
то можно использовать подстановку
![]() .
.
53.Задачи, приводящие
к понятию определенного интеграла.
Интегральные
суммы.Пусть
функция
задана на сегменте
![]() ,
,
![]() .
Обозначим символом
разбиение сегмента
при помощи некоторых несовпадающих
друг с другом точек
.
Обозначим символом
разбиение сегмента
при помощи некоторых несовпадающих
друг с другом точек
![]() на
частичных сегментов
на
частичных сегментов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Точки
,
.
Точки
,
![]() ,
,
,
,
![]() будем называть точками разбиения
.
Пусть
будем называть точками разбиения
.
Пусть
![]() - произвольная точка частичного сегмента
- произвольная точка частичного сегмента
![]() ,
а
,
а
![]() - разность
- разность
![]() ,
которую мы в дальнейшем будем называть
длиной частичного сегмента
.
,
которую мы в дальнейшем будем называть
длиной частичного сегмента
.
Определение.
Число
![]() ,
где:
,
где:

называется
интегральной
суммой
(или суммой Римана) функции
![]() ,
соответствующей разбиению
,
соответствующей разбиению
![]() сегмента
сегмента
![]() и данному выбору промежуточных точек
и данному выбору промежуточных точек
![]() на частичных сегментах
на частичных сегментах
![]() .
.
Геометрический смысл интегральной суммы – площадь ступенчатой фигуры.


Введем
обозначение
![]() .
.
Определение.
Число
называется пределом
интегральных сумм
![]() при
при
![]() ,
если для любого положительного
,
если для любого положительного
![]() можно указать такое число
можно указать такое число
![]() ,
что для любого разбиения
сегмента
,
для которого максимальная длина
,
что для любого разбиения
сегмента
,
для которого максимальная длина
![]() частичных сегментов меньше
,
независимо от выбора точек
,
на сегментах
выполняется неравенство
частичных сегментов меньше
,
независимо от выбора точек
,
на сегментах
выполняется неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Определение.:
Функция
называется интегрируемой
(по Риману) на сегменте
,
если существует конечный предел
![]() интегральных сумм этой функции при
интегральных сумм этой функции при
![]() .
Указанный предел
называется определенным
интегралом функции по сегменту
и обозначается следующим образом:
.
Указанный предел
называется определенным
интегралом функции по сегменту
и обозначается следующим образом:
 .
.
Числа и называются, соответственно, верхним и нижним пределом интегрирования, а отрезок – интервалом интегрирования.
В
случае
![]() определенный интеграл равен площади
криволинейной трапеции, границами
которой являются: ось
определенный интеграл равен площади
криволинейной трапеции, границами
которой являются: ось
![]() ,
линии
,
линии
![]() и
и
![]() ,
а также график функции
.
,
а также график функции
.
О бозначим
через
бозначим
через
![]() и
и
![]() соответственно точную верхнюю и точную
нижнюю грани этой функции на сегменте
.
соответственно точную верхнюю и точную
нижнюю грани этой функции на сегменте
.
Определение: Суммы:
![]()
и
![]()
называют соответственно верхней и нижней суммами Дарбу функции для данного разбиения сегмента .
Очевидно,
что любая интегральная сумма
![]() данного разбиения
сегмента
заключена между верхней и нижней суммой
данного разбиения
сегмента
заключена между верхней и нижней суммой
![]() и
и
![]() этого разбиения.
этого разбиения.
Свойства верхних и нижних сумм:
Для любого фиксированного разбиения и для любого промежуточные точки
 на сегментах
на сегментах
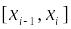 можно выбрать так, что интегральная
сумма
будет удовлетворять неравенствам
можно выбрать так, что интегральная
сумма
будет удовлетворять неравенствам
 .
Точки
на сегментах
можно выбрать также и таким образом,
что интегральная сумма
будет удовлетворять неравенствам
.
Точки
на сегментах
можно выбрать также и таким образом,
что интегральная сумма
будет удовлетворять неравенствам
 .
.Если разбиение
 сегмента
сегмента
 получено путем добавления новых точек
к точкам разбиения
этого сегмента, то для верхних и нижних
сумм этих разбиений выполнены неравенства
получено путем добавления новых точек
к точкам разбиения
этого сегмента, то для верхних и нижних
сумм этих разбиений выполнены неравенства
 и
и
 .
.Пусть и
 - любые два разбиения сегмента
- любые два разбиения сегмента
 .
Тогда если
.
Тогда если
 ,
,
 и
и
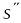 ,
,
 - соответственно нижние и верхние суммы
разбиений
и
,
то
- соответственно нижние и верхние суммы
разбиений
и
,
то
 и
и
 .
.Множество
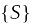 верхних сумм данной функции
для всевозможных разбиений сегмента
ограничено снизу. Множество
верхних сумм данной функции
для всевозможных разбиений сегмента
ограничено снизу. Множество
 нижних сумм ограничено сверху.
нижних сумм ограничено сверху.
Обозначим
через
![]() точную нижнюю грань множества
верхних сумм, а через
точную нижнюю грань множества
верхних сумм, а через
![]() - точную верхнюю грань множества нижних
сумм
- точную верхнюю грань множества нижних
сумм
![]() .
.
Определение:
Числа
![]() и
и
![]() называются соответственно верхним и
нижним интегралами Дарбу от функции
.
называются соответственно верхним и
нижним интегралами Дарбу от функции
.
Пусть разбиение
 сегмента
получено из разбиения
добавлением к последнему
сегмента
получено из разбиения
добавлением к последнему
 новых точек, и пусть, если
новых точек, и пусть, если
 ,
,
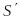 и
,
- соответственно нижние и верхние суммы
разбиений
и
.
Тогда для разностей
и
,
- соответственно нижние и верхние суммы
разбиений
и
.
Тогда для разностей
 и
и
 может быть получена оценка, зависящая
от максимальной длины
может быть получена оценка, зависящая
от максимальной длины
 частичных сегментов разбиения
,
числа
добавленных точек и точных верхней и
нижней граней
частичных сегментов разбиения
,
числа
добавленных точек и точных верхней и
нижней граней
 и
и
 функции
на сегменте
.
Именно
функции
на сегменте
.
Именно
 и
и
 .
.Лемма Дарбу: Верхний и нижний интеграл Дарбу и от функции по сегменту являются соответственно пределами верхних и нижних сумм при
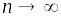 и, следовательно,
:
и, следовательно,
:
 ,
,
 ,
и при этом
,
и при этом
![]() .
.
54. Свойства определенного интеграла. Будем считать, что определенный интеграл с одинаковыми пределами интегрирования равен нулю (по определению):
 .
.
Будем считать, что при перемене мест верхнего и нижнего пределов интегрирования определенный интеграл меняет знак на противоположный:
 .
.
Пусть функции и
 интегрируемы на сегменте
,
тогда функции
интегрируемы на сегменте
,
тогда функции
 ,
,
 и
и
 также интегрируемы на этом сегменте,
причем:
также интегрируемы на этом сегменте,
причем:
 .
.
Если функция интегрируема на сегменте , то функция
 (
( =const)
интегрируема на этом сегменте, причем:
=const)
интегрируема на этом сегменте, причем:
 .
.
Если функция интегрируема на сегменте , то эта функция интегрируема на любом сегменте
 ,
содержащемся в сегменте
.
,
содержащемся в сегменте
.Пусть функция интегрируема на сегментах
 и
и
 .
Тогда эта функция интегрируема на
сегменте
,
причем:
.
Тогда эта функция интегрируема на
сегменте
,
причем:
 .
.
55.Формула Ньютона-Лейбница. Из этих равенств вытекает соотношение:
 ,
,
которое называется основной формулой интегрального исчисления или формулой Ньютона – Лейбница.
Пусть выполнены следующие условия:
1) Функция непрерывна на отрезке ;
2)
отрезок
является множеством значений некоторой
функции
![]() ,
определенной на отрезке
,
определенной на отрезке
![]() и имеющей на этом отрезке непрерывную
производную;
и имеющей на этом отрезке непрерывную
производную;
3)
![]() ,
,
![]() .
.
При этих условиях справедлива формула:

Указанная формула называется формулой замены переменной в определенном интеграле.
Пусть
функции
![]() и
и
![]() имеют непрерывные производные на
сегменте
.
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
имеют непрерывные производные на
сегменте
.
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
 .
.
Так
как
![]() и
и
![]() ,
то эту формулу можно записать следующим
образом:
,
то эту формулу можно записать следующим
образом:
 .
.
56.Замена переменной
в определенном интеграле.Теорема:Если
функция f(x)
непрерывна на[a;b],а
x= (t)
непрерывна на отрезке вместе со своей
x'(t)=
'(t)
на [α;β],где x(α)=
(α)=a,x(β)=
(β)=b,
то
(t)
непрерывна на отрезке вместе со своей
x'(t)=
'(t)
на [α;β],где x(α)=
(α)=a,x(β)=
(β)=b,
то

57.Вычисление
площади плоских фигур.
Определение:
Плоская
фигура
![]() – часть плоскости, ограниченная простой
замкнутой кривой
– часть плоскости, ограниченная простой
замкнутой кривой
![]() ,
при этом кривая
называется границей фигуры
.
,
при этом кривая
называется границей фигуры
.
Определение: Мы будем говорить, что многоугольник вписан в фигуру , если каждая точка этого многоугольника принадлежит фигуре или ее границе.
Определение: Если все точки плоской фигуры и ее границы принадлежат некоторому многоугольнику, то мы будем говорить, что указанный многоугольник описан вокруг фигуры .
Замечание: Площадь любого вписанного в фигуру многоугольника не больше площади любого описанного вокруг фигуры многоугольника.
Пусть
![]() - числовое множество площадей вписанных
в плоскую фигуру
многоугольников, а
- числовое множество площадей вписанных
в плоскую фигуру
многоугольников, а
![]() - числовое множество площадей описанных
вокруг плоской фигуры
многоугольников. Очевидно, что множество
ограничено сверху (площадью любого
описанного вокруг фигуры
многоугольника), а множество
ограничено снизу (например, числом
нуль).
- числовое множество площадей описанных
вокруг плоской фигуры
многоугольников. Очевидно, что множество
ограничено сверху (площадью любого
описанного вокруг фигуры
многоугольника), а множество
ограничено снизу (например, числом
нуль).
Обозначим
через
![]() точную верхнюю грань множества
,
через
точную верхнюю грань множества
,
через
![]() точную нижнюю грань множества
.
точную нижнюю грань множества
.
Числа и называются соответственно нижней площадью и верхней площадью фигуры
Замечание:
Нижняя площадь
фигуры
не больше верхней площади
,
т. е.
![]() .
.
Определение.
Плоская фигура
называется квадрируемой,
если верхняя площадь этой фигуры
совпадает с ее нижней площадью. При этом
число
![]() называется площадью
фигуры
.
называется площадью
фигуры
.
Теорема:
Для
того чтобы плоская фигура
была квадирируемой, необходимо и
достаточно, чтобы для любого положительного
числа
![]() можно было указать такой описанный
вокруг фигуры
многоугольник и такой вписанный в фигуру
многоугольник, что разность
можно было указать такой описанный
вокруг фигуры
многоугольник и такой вписанный в фигуру
многоугольник, что разность
![]() площадей которых была бы меньше
,
площадей которых была бы меньше
,
![]() .
.
Определение:
Криволинейной
трапецией
называется фигура, ограниченная графиком
заданной на сегменте
непрерывной и неотрицательной функции
,
ординатами, проведенными в точках
![]() и
и
![]() ,
и отрезком оси
,
и отрезком оси
![]() между точками
и
.
между точками
и
.
Теорема:
Криволинейная трапеция представляет
собой квадрируемую фигуру, площадь
![]() которой может быть вычислена по формуле:
которой может быть вычислена по формуле:
 .
.
