
- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
Опр.
Число
назыв. целым алгебраическим числом
(ц.а.ч.), если оно явл. корнем многочл.
с целыми кофиц., нормированного,
неприводимого над полем
.
Многочл.
явл.
многочл. для ц.а.ч.
.
Т.
Пусть дано множество
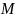 - всех ц.а.ч.. Это множество
образует кольцо. Док.:
Рассмотрим
- всех ц.а.ч.. Это множество
образует кольцо. Док.:
Рассмотрим
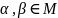 .
Пусть
.
Пусть
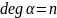 ,
а
,
а
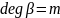 .
И пусть
для
,
и
.
И пусть
для
,
и
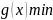 для
.
И обозначим
чила сопряженные с
,
а через
для
.
И обозначим
чила сопряженные с
,
а через
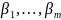 числа сопряженные с
.
Составим 2 многочл.
числа сопряженные с
.
Составим 2 многочл.
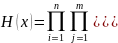 ,
,
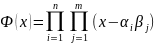 .
Если в
.
Если в
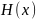 переставить
переставить
 или
или
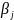 ,
то от этого многочл.
– не изменится, а это означает. что
кофиц. многочл.
явл. симметр. многочл. по двум систем.
перемен. котор. явл. корнями многочл.
и
с целыми кофиц. и старшим кофиц. равный
1. По следствию из теоремы об основных
симметрич. многочл. значения этих же
кофиц. от корней многочл.
,
то от этого многочл.
– не изменится, а это означает. что
кофиц. многочл.
явл. симметр. многочл. по двум систем.
перемен. котор. явл. корнями многочл.
и
с целыми кофиц. и старшим кофиц. равный
1. По следствию из теоремы об основных
симметрич. многочл. значения этих же
кофиц. от корней многочл.
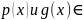 кольцу целых чисел, т.е. явл. целыми
числами. Старший кофиц.
равен 1, поэтому все корни этого многочл.
явл. ц.а.ч.. В часности
кольцу целых чисел, т.е. явл. целыми
числами. Старший кофиц.
равен 1, поэтому все корни этого многочл.
явл. ц.а.ч.. В часности
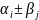 - корни многочл.
явл. ц.а.ч. следовательно
- корни многочл.
явл. ц.а.ч. следовательно
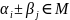 .
Аналогично показыв. что
.
Аналогично показыв. что
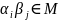 ,
а т.к. для чисел
и
,
,
а т.к. для чисел
и
,
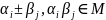 и
явл. числовым множеством, то
- кольцо.
и
явл. числовым множеством, то
- кольцо.
27.Разрешимость алгебраических уравнений в квадратных радикалах.
При
решении задач на построение используются
только циркуль и линейка. С
помощью циркуля и линейки можно построить
по заданным отрезкам
 и
и
 :
1)
:
1)
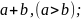 2)
2)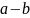 ;
3)
;
3)
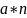 ;
4)
;
4)
 ;
5)
;
5)
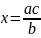 (четвертый
пропорциональный отрезок); 6) среднее
геометрическое. Четыре
этапа построения:
1) анализ; 2) построение; 3) доказательство;
4) исследование. Методы
решения задач на построение:
1) геометрический; 2) спряжение; 3) подобие;
4) параллельный перенос; 5) симметрия; 6)
поворот, и т.д. Многие задачи на построение
сводятся к нахождению корней уравнений.
Квадратные
радикалы.
Рассмотрим уравнение
(четвертый
пропорциональный отрезок); 6) среднее
геометрическое. Четыре
этапа построения:
1) анализ; 2) построение; 3) доказательство;
4) исследование. Методы
решения задач на построение:
1) геометрический; 2) спряжение; 3) подобие;
4) параллельный перенос; 5) симметрия; 6)
поворот, и т.д. Многие задачи на построение
сводятся к нахождению корней уравнений.
Квадратные
радикалы.
Рассмотрим уравнение
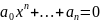 (1)
.
Уравнение (1) разрешимо в квадратных
радикалах над полем
,
если все его корни можно выразить через
элементы поля
,
с помощью операций +,-, возведения в
степень и извлечения корня. Абель доказал
что не ∃
универсальной формулы решения в
квадратных радикалах алгебр. уравнений
степени больше 4. Глуа доказал критерий
разрешимости уравнений в квадратных
радикалах ∀
степени. Опр.
Расширение
(1)
.
Уравнение (1) разрешимо в квадратных
радикалах над полем
,
если все его корни можно выразить через
элементы поля
,
с помощью операций +,-, возведения в
степень и извлечения корня. Абель доказал
что не ∃
универсальной формулы решения в
квадратных радикалах алгебр. уравнений
степени больше 4. Глуа доказал критерий
разрешимости уравнений в квадратных
радикалах ∀
степени. Опр.
Расширение
 поля
назыв. квадрат., если
поля
назыв. квадрат., если
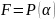
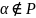 ,
но
,
но
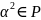 .
.
28.Область рациональности. Теорема (с док-вом).
Опр.
Областью
рациональности назыв. множество чисел
полученных из кофиц. уравнения
(1) и системы рацион. чисел. с помощью 4
математ. операций +,-,*,/, кроме деления
на 0. З!
Каждое уравнение имеет свою область
рациональности (обозначается
)
и область рациональности явл. полем. Т.
Корень
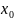 уравнения (1) с комплексными кофиц. выраж.
через квадратные радикалы
уравнения (1) с комплексными кофиц. выраж.
через квадратные радикалы
 ,
,
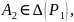
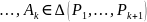 ,
,
 . Док.:
Необх.:
Пусть
выраж. через квадратные радикалы
. Док.:
Необх.:
Пусть
выраж. через квадратные радикалы
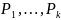 ,
тогда
получается с помощью 4 арефмет. действия
над радикалами
из кофиц. (1) и рацион. чисел. Т.к. все
расширению
,
тогда
получается с помощью 4 арефмет. действия
над радикалами
из кофиц. (1) и рацион. чисел. Т.к. все
расширению
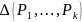 и
- есть поле, то
и
- есть поле, то
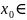 области рациональности. Дост.:
Пусть
области рациональности. Дост.:
Пусть
 . Т.к.
выраж. через
,
то
выражается через кофиц. уравнения (1) и
через рацион. числа.⊠
. Т.к.
выраж. через
,
то
выражается через кофиц. уравнения (1) и
через рацион. числа.⊠
