27. Формула Ньютона-Лейбница.

Пусть Ф^’(х)=f(x) и F’(х)=f(х) - др первообр.

Ф(х)=F(x)+C, =F(x)+C, где С- некоторое число, axb. Подставляя в это равенство значение х=а и используя свойство 1, имеем: =0, получим: 0= , F(a)+C, C=-F(a)

Т.е. для любого х[a,b] Полагая здесь х=b получим искомую формулу.

Замечание 1.В качестве F(х) можно взять любую первообр для f(х) на отрезке [a,b].

Замечание 2. Ф-ла Ньютона-Лейбница явл методом вычисления опр интеграла.

28. Замена переменных в определенном интеграле.

[T] пусть функция f(x) непрерывна на [a,b] и пусть выполнены следующие условия:

1. функцию х=(t) дифференцируема на [,] и ’(t) непрерывна на [,]

2. Множеством значений функции х=(t) является отрезок [a,b]

3. ()=a и ()=b, то справедлива формула

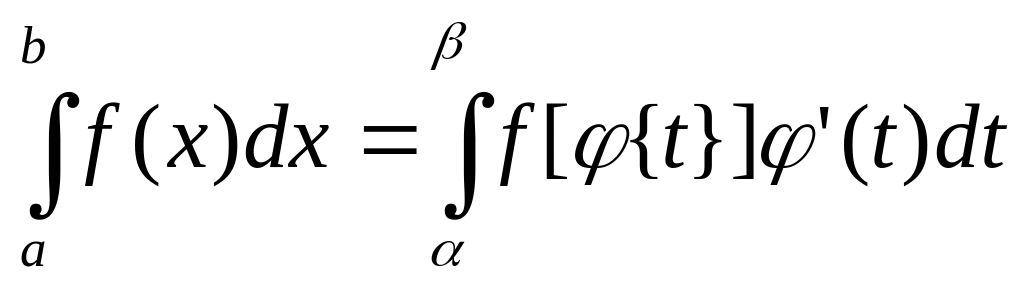
Доказательство: По формуле Ньютона- Лейбница:

Пусть F(x)- первообразная для функции f(x) на [a,b].

Рассмотрим сложную функцию Ф(t)=F((t)) Согласно правилу дифференцирования сложной функции находим: Ф’(t)=F’((t))*’(t)=f((t))’(t). Отсюда следует, что функция Ф(t) является первообразной для функции f((t))’(t), непрерывной на [,] и поэтому согласно формуле Ньютона-Лейбница получаем, = Ф()-Ф()=F(())-F(())=F(b)-F(a)=

Замечание1. При исп-нии данной ф-лы не надо возвращ от новой переем-ной t к старой х.

Замечание 2. При исп-нии ф-лы надо проверять соблюдение всех условий.

Формула интегрирования по частям в определенном интеграле.

[T] Если функция u(x) и v(x) имеют непрерывные производные на [a,b] то справедлива формула

Доказательство Так как функция u(x) и v(x) по условию имеют производные, то по правилу дифференцирования произведения [u(x)v(x)]’=u(x)v’(x)+v(x)u’(x). Откуда следует, что функция u(x)v(x) является первообразной для функции u(x)v’(x)+v(x)u’(x). Тогда по формуле Ньютона-Лейбница Отсюда , ч т.д.

29. Приложение определенного интеграла: площадь криволин трапеции,длина дуги плоской кривой,объем тела вращения и площадь поверхности.

Рассмотрим плоскую фигуру, ограниченную [a,b] оси Ох, прямыми x=a, x=b и графиком непрерывной и неотрицательной функции y=f(x) на [a,b]. S=

Геометрический смысл определнного интеграла: определенный интеграл от неотрицательной непрерывной функции f(x) на [a,b] численно равен площади криволинейной трапеции.

30. Несобственные интегралы с бесконечными пределами.

Пусть функция f(x) определена на промежутке [a; +) и интегрируема на любом отрезке [a,R], R>0, так что интеграл имеет смысл, Предел этого интеграла при R называется несобственным интегралом первого рода и обозначается (1). В случае, если этот предел конечен, говорят, что несобственный интеграл сходится, а функцию f(x) называют интегрируемой на бесконечном промежутке [a, +), если же предел бесконечен или не существует, то говорят, что несобственный интеграл расходится.

Аналогично вводится понятие несобственного интеграла по промежутку (-, b]. . Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов , где с- любое число.

Геометрический смысл несобственного интеграла первого рода состоит в том,что несобств интеграл первого рода-это площадь соотв заштрих бесконечной области.