
- •Пространство Rn.
- •Сходимость последовательности в Rn.
- •Открытые,замкнутые.Компактные мн-ва Rn.
- •Понятие функции n переменный. Предел функции n переменных.
- •Частные производные функции n переменных.
- •Дифференцируемость функции n переменных.
- •Дифференциал функции n переменных.
- •Дифференцирование сложной функции.
- •Неявные функции.
- •Производная по направлению. Градиент.
- •Частные производные высших порядков функции n переменных.
- •Локальный экстремум. Необходимые условия.
- •Достаточные условия локального экстремума функции n переменных.
- •Теорема о разрешимости системы функциональных уравнений.
- •Условный экстремум
- •Метод множителей Лагранжа.
- •Понятие первообразной. Основные свойства (лемма, теорема)
- •23. Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
- •Понятие неопределенного интеграла.
- •Основные методы интегрирования.Рекурентные формулы.
- •Непосредственное интегрирование.
- •Метод подстановки или метод замены переменных.
- •Метод интегрирования по частям.
- •Интегрирование рациональных функций
- •Интегрирование иррац. И трансцендентных функций.
- •Понятие определенного интеграла.
- •Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
- •Основные свойства определенного интеграла.
- •Оценки интегралов. Формула среднего значения.
- •Интеграл с переменным верхним пределом.
- •Формула Ньютона-Лейбница.
- •Замена переменных в определенном интеграле.
- •Приложение определенного интеграла: площадь криволин трапеции,длина дуги плоской кривой,объем тела вращения и площадь поверхности.
- •Несобственные интегралы с бесконечными пределами.
- •Несобственные интегралы от неограниченных функций.
- •Признаки сходимости несобственных интегралов.Примеры.
- •Определние и услвия сущ-ния двойных интегралов.Геом смысл.Св-ва.
- •Сведение двойного интеграла к повторному(2случая).
- •2Сл. Теорема о переходе от к повторному для криволинейной обл-ти.
- •Определение числового ряда, частичной суммы, сходящегося ряда.
- •Свойства сходящихся числовых рядов.
- •Необходимое условие сходимости числового ряда. Сходимость гармонического ряда.
- •38. Ряды с неотрицательными членами. Признак сходимости.
- •Признак сравнения.
- •Признак Даламбера.
- •Знакочередующийся ряд. Признак Лейбница.
- •Знакопеременные ряды, их сходимость.
- •Степенные ряды.
- •Разложение ф-ии в степенные ряды.Ряды Тейлора и Маклорена.
- •Диффер ур-ния 1-го порядка.Решение ур-ния.Теорема Коши и ее геом смысл.
- •Общее и частное решение диффер ур-ния.
Дифференциал функции n переменных.
Дифференциалом du дифференцируемой в точке М(х1,х2,…,хn) функции u=f(x1,x2,…,xn) называется главное линейное относительно приращения аргумента часть приращения этой функции в точке М.
Если все коэффициенты Ai=0, то дифференциал функции в точке М считается равным 0.
Как
и в случае 1 перем-ой будем считать,что
дифференциал от независимой переменной
совпадает с ее приращением,т.е. d'xi=![]() i=
.
du=
i=
.
du=![]() (*)
(*)
Замечание1. Ф-ла (*) выписана для случая,когда пргументы хi явл независ переменными.Далее будет доказано,что ф-ла справедлива и в случае,когда хi-зависимые переменные (это св-во назыв инвариантность формы первого диффер-ла).
Замечание2. Геометр смысл диф-ла 2х переменных. (рис.)
Дифференцирование сложной функции.
Рассмотрим вопрос о дифференцировании сложной функции нескольких переменных вида:
U=f(M)=f(X1,x2,…xn) (1)
Xi=i(t1,t2,…,tk), I=1,2,…m (2)
[T]
Пусть функция (2) дифференцируема в
некоторой точке Nо
(![]() ,
а функция (1) дифференцируема в точке
Мо(
,
а функция (1) дифференцируема в точке
Мо(![]() ,
причем
,
причем
![]() Тогда сложная функция u=f(x1,x2,…,xn),
где Х1,Х2,…,Хn
определяется по формулам (2) дифференцируема
в точке Мо, при этом частные производные
этой сложной функции вычисляются по
формулам:
Тогда сложная функция u=f(x1,x2,…,xn),
где Х1,Х2,…,Хn
определяется по формулам (2) дифференцируема
в точке Мо, при этом частные производные
этой сложной функции вычисляются по
формулам:
![]()
….
![]()
в
которых
![]() берутся в точке Mо,
а частные производные
берутся в точке Mо,
а частные производные
![]() берутся
в точке Nо.
берутся
в точке Nо.
Следствие:
Случай,когда ф-ла (2) зависит только от
t1
хi=φi(t),поэтому
ф-ла примет вид
![]()
Неявные функции.
D'ef Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.
Частные производные неявно заданной функции вычисляются по формулам:
d'u/d'xi=-(d'F/d'xi)/(d'F/d'u), i=1,...,n
Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:
/u1=ф1(х1,х2,...,хn)
/u2=ф2(х1,х2,...,хn) (1)
\...
\um=фm(х1,х2,...,хn)
Пусть функции определены, как решение М функциональных уравнений (2)
(2)
/F1(u1,...,um,x1,...xn)=0
/F1(u1,...,um,x1,...xn)=0 (2)
\...
\F1(u1,...,um,x1,...xn)=0
Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.
D'ef Это решение будем называть непрерывным и дифференцируемом в некоторой области D' изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.
ld'F1/d'u1, d'F1/d'u2,..., d'F1/d'un l
ld'F2/d'u1, d'F2/d'u2,..., d'F2/d'un l = D'(F1,F2,...,Fn)\D'(u1,u2,...,un)
l... l
ld'Fm/d'u1, d'Fm/d'u2,..., d'Fm/d'unl
Такой определитель называют определителем Якоби или Якобианом.
[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, d'Fi/d'ui непрерывна в точке Мо, D'(F1,F2,...,Fn)\D'(u1,u2,...,un)
Якобиан отличен от 0 и F1=F2=…=Fn в точке Мо
Производная по направлению. Градиент.
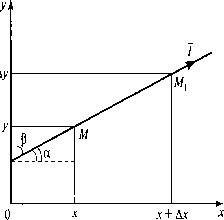
Рассмотрим
функцию трех переменных u=f(x,y,z).
Пусть она определена в некоторой
окрестности точки Мо(хо,yo,zo).
Рассмотрим всевозможные лучи, выходящие
из точки Мо. Каждый такой луч заадется
единственным вектором (соs,
cos,cos).
Если l-
длина этого отрезка, то его координаты
![]() (lcos,
lcos,
lcos)
C
другой стороны:
(x-xo,
y-yo,
z-zo)
(lcos,
lcos,
lcos)
C
другой стороны:
(x-xo,
y-yo,
z-zo)
Т.о. получили один и тот же отрезок:
Приравняем
![]()
u=f(Xo+lcos, Yo+lcos, Zo+lcos) (1)
Т.о. u- сложная функция.
Производную
указанной сложной функции по переменной
l,
взятую в точке l=0
нназывают производной функции u=f(x,y,z)
в точке Мо по направлению, оопределяемому
единичным вектором l.
Обозначение:
![]()
(2)
Градиентом
функции u=f(x,y,z)
в данной точке Мо(xo,yo,zo)
называется вектор, координаты которого
имеют вид gradu(Mo)=![]()
Если: u=f(x1,x2,…,xn) Mo(
[Т] Вектор градиента функции y=f(x,y,z) в точке Мо характеризует направление и величину максимального роста функции в точке Мо,т.е. производные функции u=f(x,y,z) в точке Мо по направлению, определенному вектором градиента этой функции в точке Мо имеет максимальное значение по сравнению с производной по любому другому направлению и это значение равно длине вектора градиента.
Док-во: Из ф-л (1) и(2) →(gradu,e) =∂u/∂e
∂u/∂e=(gradu,e) = |gradu|*|e|*cosφ
Cosφ=1 φ=0
Max значение достигается ↔ вектор е и вектор grad направлены одинаково. Тогда |∂u/∂e=gradu|
Следствие. Вектор градиента не зависит от выбора координат.
Геометрический смысл градиента:
Линии уровня для функции двух переменных u=f(x,y) называется линия на которой функция сохраняет свое постоянное значение.
Если В каждой точке линии уровня M(xо,yо) построить касательную, то вектор-градиент в точке Мо будет перпендикулярен этой касательной.
Поверхность уровня- фунция u=f(x,y,z) в точке Мо (xo,yo,zo) называется поверхность на которой функция сохраняет свое постоянное значение.
Свойства: если в каждой точке Mo(xo,yo,zo) провести касательную поверхность, то вектор градиент будет ортогонален этой поверхности.
