Несобственные интегралы от неограниченных функций.
Определение1.Пусть f(x), определенную на отрезке(a,b],иограниченна на на любом отрезке [a+,b], 0< <b-a,. В таком случае х=а называется особой точкой.
Определение2.
Пусть функция f(x)
определена на промежутке (a,b],
если особой является точка х=а, и сущ.
конечный предел то несобственных
интеграл второго рода определяется как
При
этом говорят, что несобственный интеграл
сходится, если же предел не сущ или равен
бесконечности, то говорят что несобствен.
интеграл расходится
Определение3.Точка х=в явл. особой точкой для f(х), если f(x) неогран. В любой окрестности данной точки, но огран на любом отрезке [а.b-] для всех >0 таких что a<b-<b
Определение4.
Пусть х=в особая точка для f(x)
определенной на[a,b)
тогда если сущ конечный предел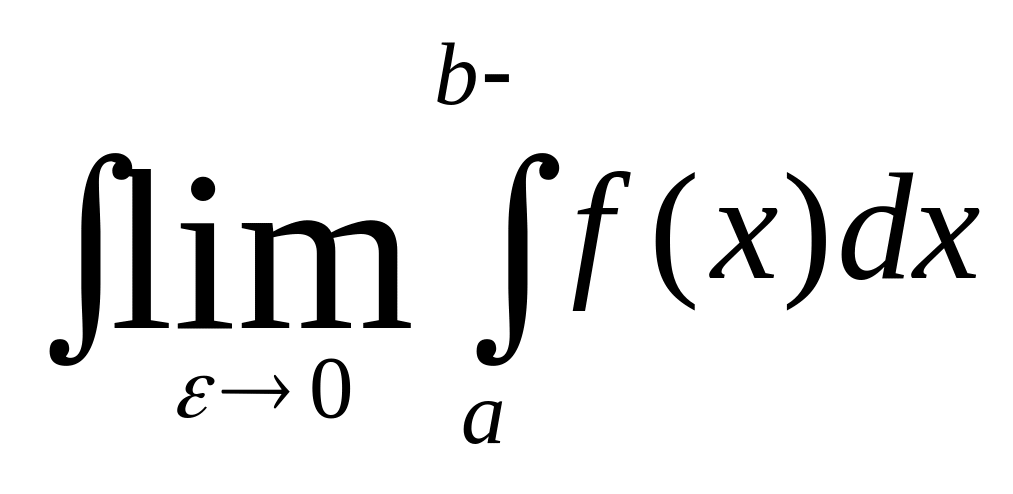
то
он называется несобствен интегралом
второго родап и обознач.
Определение5. Если а и b особые точки, т.е. функция С ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы , где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.
Определение6. f(x) определена на отрезке (a,b) за искл. точки d которая назыв особой опред. Как сумма двух несобственных интегралов.При условии что оба интграла сущ.
Признаки сходимости несобственных интегралов.Примеры.
Теорема (признак сравнения несобственных интегралов). Пусть функции f(x) и g(x) непрерывны на промежутке [a , ∞) и удовлетворяют на нём условию 0 ≤ f(x) ≤ g(x). Тогда из сходимости интеграла a ∫ ∞g(x) dx (1) следует сходимость интеграла a∫∞f(x)dx (2) и наоборот, из расходимости интеграла(2) следует расходимость интеграла (1).Доказательство: Введём обозначения F(R)=a∫Rf(x)dx, G(R)=a∫Rg(x)dx, причём 0≤F(R)≤G(R).
Функции F(R) и G(R) являются неубывающими; в самом деле, если a≤R1≤R2, то R1∫R2f(x)dx≥0 и тогда F(R2)=a∫R2 f(x)dx=a∫R1f(x)dx+R1∫R2f(x)dx≥a∫R1f(x)dx=F(R1).
Возьмём последовательность значений {Rn}→∞; тогда соответствующая последлвательность значений функции {F(Rn)} является монотонной и неубывающей. Пусть интеграл (1) сходится, тогда последовательность {G(Rn)} ограничена, но тогда ограничена и последовательность {F(Rn)}, а значит в силу теоремы(монотонная ограниченная последовательность сходится)она сходится. Следоавтельно, существует предел F(R) при R→∞, т.е. интеграл (2) сходится.
Теперь докажем вторую часть теоремы: пусть интеграл(2) расходится. Если предположить, что интеграл (1) сходится, то по доказанному выше интеграл(2) также должен сходится, что противоречит условию. Теорема доказана.
ЗАМЕЧАНИЕ. Аналогичный признак сравнения справедлив и для несобственных интегралов второго рода. Если функция f(x) и g(x) непрерывны на полуинтервале [a,b) и для всех точек в окресности особо точки b выполняются условия0≤f(x)≤ g(x), то из сходимости интеграла a∫b g(x)dx следует сходимость интеграла a∫b f(x)dx, а из сходимости интеграла a∫bf(x)dx следует расходимость интеграла a∫bg(x)dx.
ТЕОРЕМА (критерий Коши). Для сходимости несобственного интеграла(2) необходимо и достаточно, чтобы для любого ε>0 можно было найти такое A>0, что для любых R' и R'', больших, чем A, выполняется неравенство |F(R'')-F(R')=|R’∫R’’ f(x)dx|<ε