24.Нахождение частных решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами по виду правой части.

Рассматривается примером, но тут сразу описано нахождение искомого частного решения. Пример 1Найти общее решение дифференциального уравнения. Решение: 1)Сначала найдем общее решение соответствующего однородного уравнения. Берём наш неоднородный диффур  и обнуляем правую часть: Составим и решим характеристическое уравнение:  – получены различные действительные корни, поэтому общее решение: 2) Теперь нужно найти какое-либо частное решение  неоднородного уравнения И вопрос, который нужен: В каком виде нужно искать частное решение ? Прежде всего, смотрим на нашу правую часть: . Тут у нас многочлен третьей степени. По идее, частное решение тоже следует искать в виде многочлена третьей степени: , где  – пока ещё неизвестные коэффициенты (числа). Вариант подбора, который «сразу приходит в голову», неформально будем называть обычным, обыкновенным или штатным случаем.После предварительного анализа смотрим на корни характеристического уравнения , найденные на предыдущем этапе: это различные действительные корни, отличные от нуля. Частное решение неоднородного уравнения нужно искать в виде: После правильно выбранного подбора алгоритм пойдёт. Используем метод неопределенных коэффициентов. Найдём первую и вторую производную: Подставим  и  в левую часть неоднородного уравнения: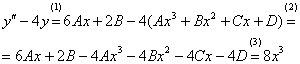 (1) Выполняем подстановку  и .(2) Раскрываем скобки.(3) После максимальных упрощений ставим знак равенства и приписываем нашу правую часть .Далее работаем с последним равенством – необходимо приравнять коэффициенты при соответствующих степенях и составить систему линейных уравнений. В картинках процесс выглядит так:

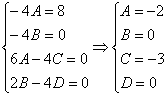
Чтобы было еще проще, рекомендую предварительно сгруппировать подобные слагаемые: , и только потом составлять систему.Подставляем найденные значения  в наш исходный подбор частного решения => Таким образом, подобранное частное решение неоднородного уравнения: 3) Запишем общее решение неоднородного уравнения: Всё! Ответ: общее решение:

25.Числовой ряд и его сумма; сходящиеся и расходящиеся ряды.

Числовой ряд – это сумма членов числовой последовательности вида . В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: 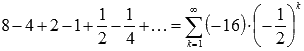. называют общим членом числового ряда или k–ым членом ряда.Для предыдущего примера общий член числового ряда имеет вид 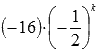.Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть, .Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.Так же тиун даёт: к расходящимся рядам относятся, например, ряды со следующими общими членами: u_n=n, u_n=n², u_n=√n, u_n=(n+1)/n, u_n=(-1)ⁿ⁺¹

26.Геометрический и гармонические ряды.

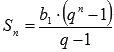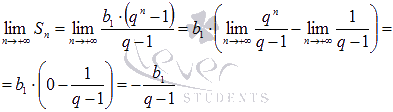Сумма геометрической прогрессии вида со знаменателем q является сходящимся числовым рядом, если , и расходящимся рядом при .(в книге тиуна b1 это aи ≠0 и q≠0) Докажем это.Мы знаем, что сумма первых n членов геометрической прогрессии находится по формуле .При справедливо что указывает на сходимость числового ряда. При q = 1 имеем числовой ряд . Его частичные суммы находятся как , а предел частичных сумм бесконечен , что указывает на расходимость ряда в этом случае.Если q = -1, то числовой ряд примет вид 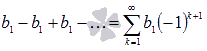. Частичные суммы принимают значение для нечетных n, и для четных n. 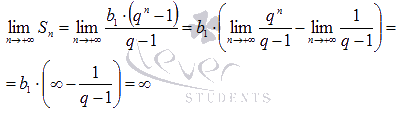Из этого можно сделать вывод, что предел частичных сумм не существует и ряд расходится.При справедливо что указывает на расходимость числового ряда. Гармонический ряд является расходящимся. Докажем расходимость гармонического ряда. Предположим, что ряд сходится. Тогда существует конечный предел его частичных сумм. В этом случае можно записать и , что приводит нас к равенству . 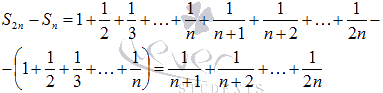С другой стороны, Не вызывают сомнения следующие неравенства . Таким образом, . Полученное неравенство указывает нам на то, что равенство не может быть достигнуто, что противоречит нашему предположению о сходимости гармонического ряда. Вывод: гармонический ряд расходится.