Свойства неопределённого интеграла

        Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если         , то 

        Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению 

        Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы 

        Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов 

        Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов 

        Свойство 6. Постоянный множитель можно выносить за знак интеграла 

        Свойство 7. Если 

то 

3.Таблица интегралов.

1. 

2. ,

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. ,

14. 

15. 

16. 

17. 

18. 

19. 

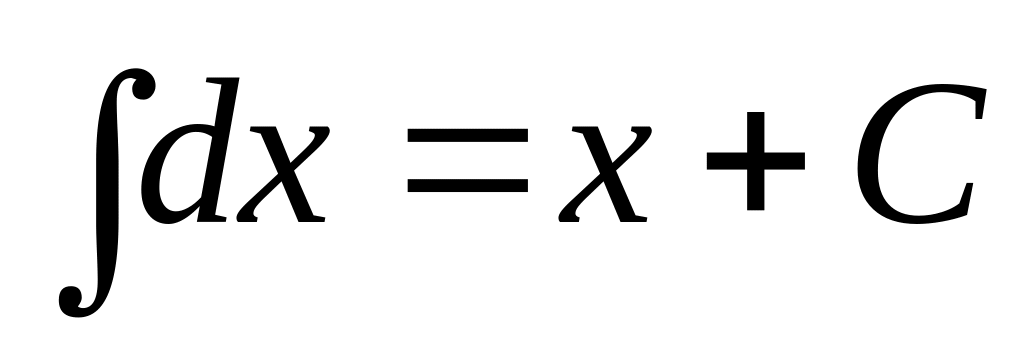
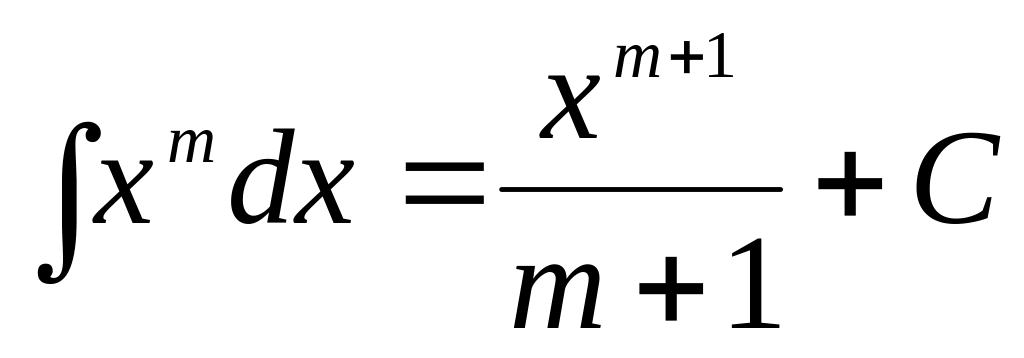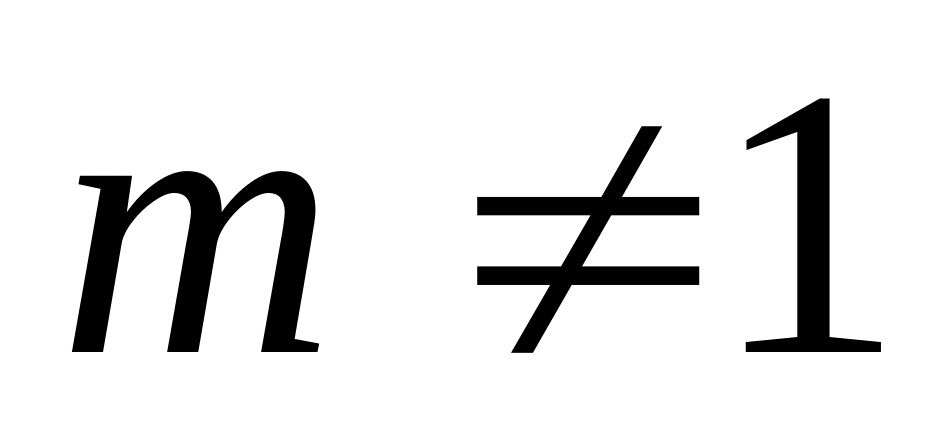
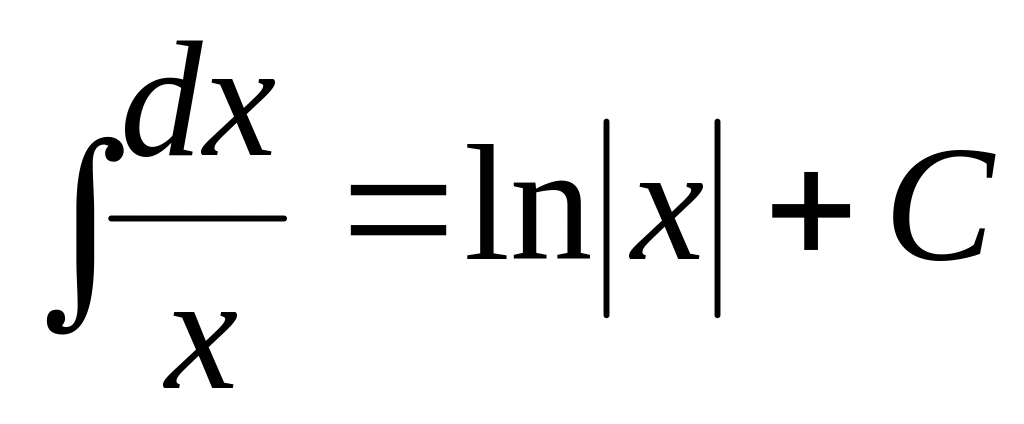
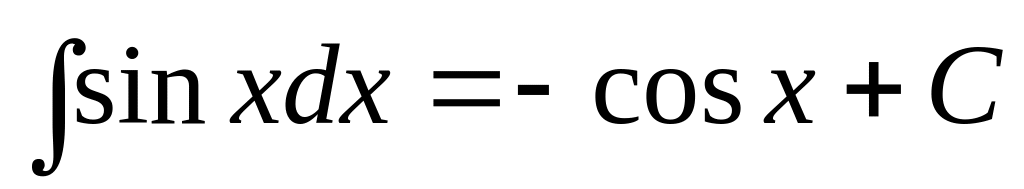
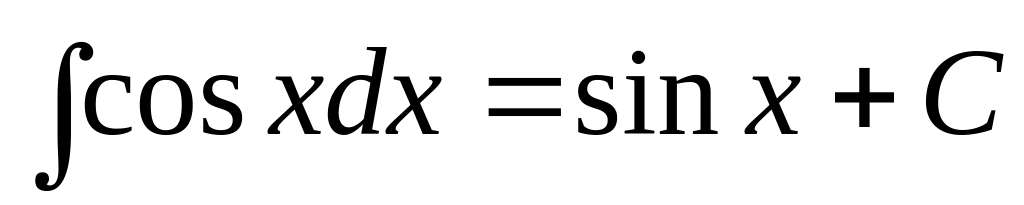
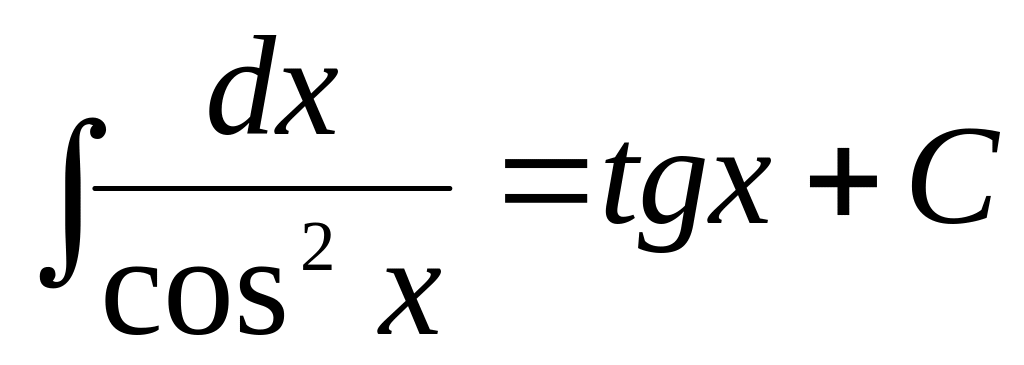
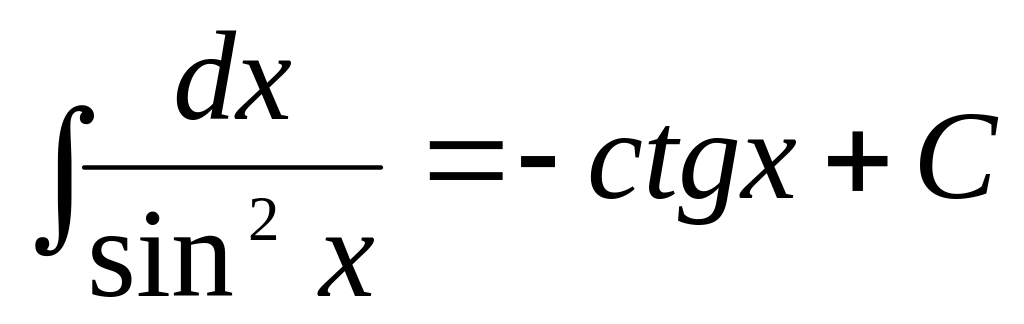
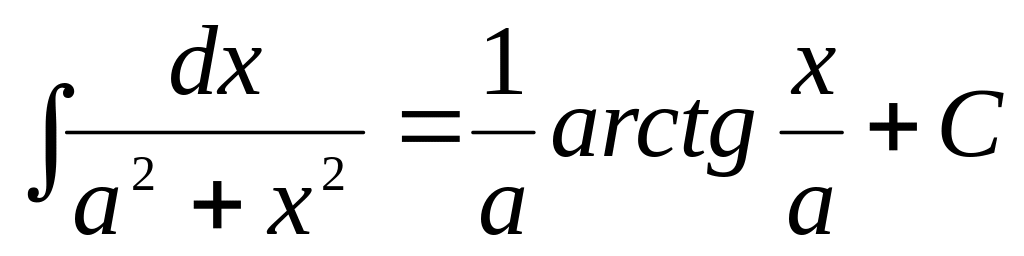
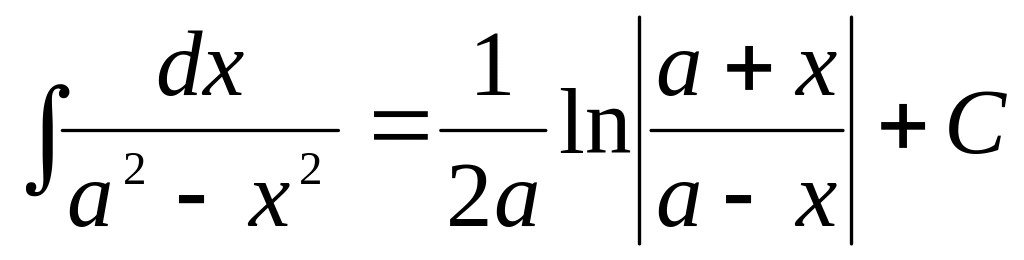
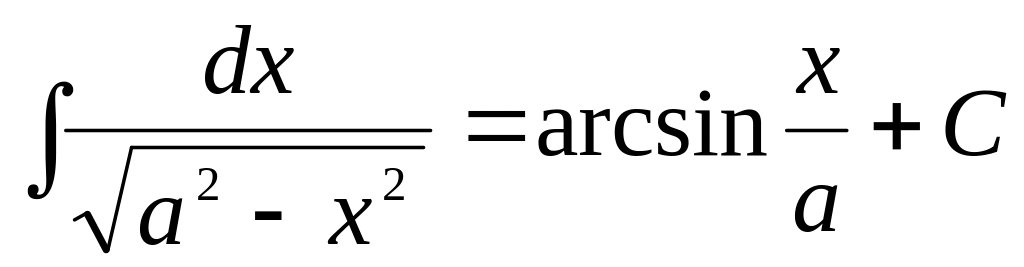
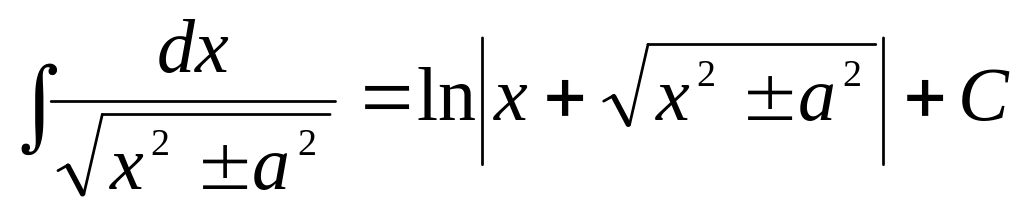
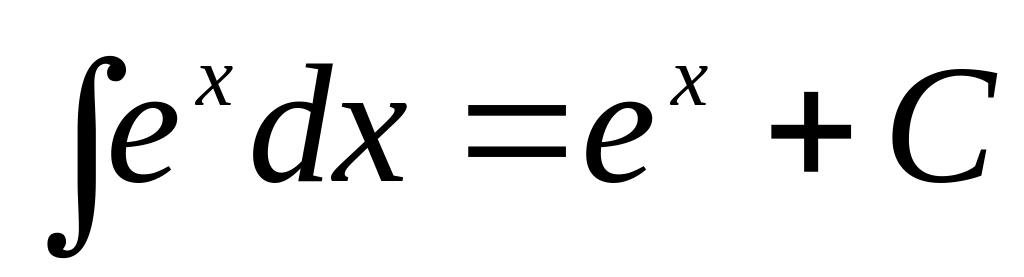
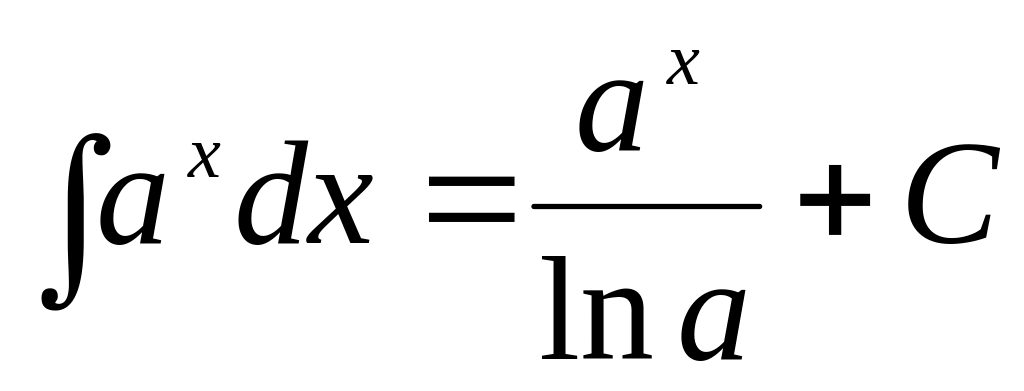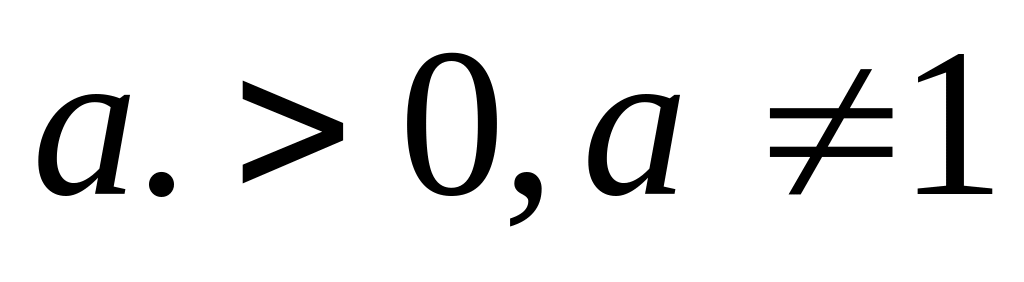
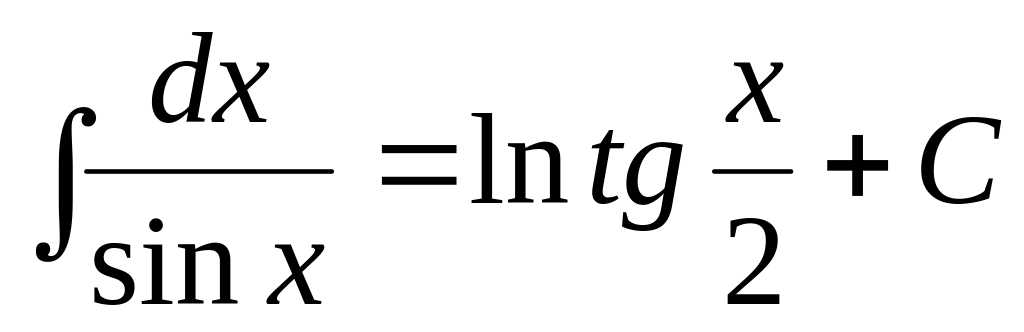
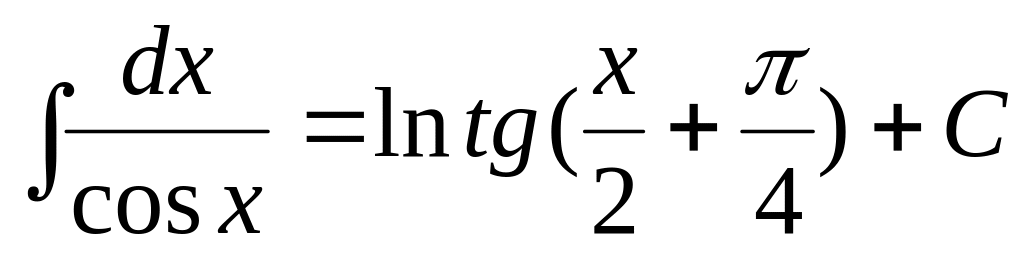
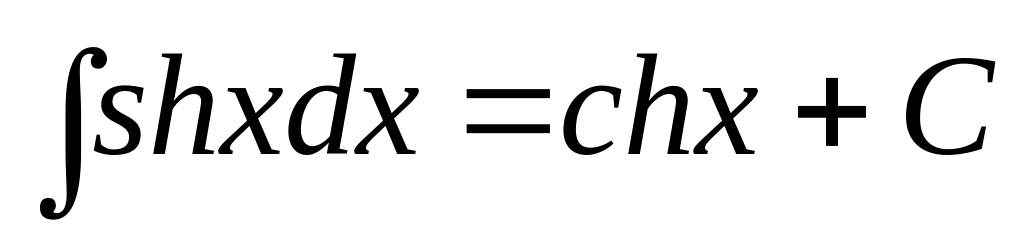
4.Замена переменной в неопределенном интеграле.

Если функция имеет непрерывную производную, то в

неопределённом интеграле можно перейти к новой переменной t по формуле

,

затем найти интеграл и вернуться к исходной переменной х. Такой способ нахождения интеграла называется методом замены переменной или методом подстановки.

Пусть F(x) –первообразная для f(x) на (a,b), функция  и    .

Тогда справедлива формула:

Доказательство. Докажем, что    .

Действительно, по правилу дифференцирования сложной функции 

 

Следовательно, функция   есть первообразная для   на  .

Замечание. Формулу замены переменных следует понимать так: при замене переменной   множество первообразных для f(x) на (a,b) переходит во множество первообразных для  на  .

5.Интегрирование по частям в неопределенном интеграле.

Интегрированием по частям называется нахождение интеграла по формуле

,

где u(x) и v(x) - дифференцируемые функции.

Применение её целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. В некоторых случаях формулу необходимо применять несколько раз.

При этом за u(x) берётся такая функция, которая при дифференцировании упрощается, а за dv -та часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например,

для интегралов вида , ,

за u(x) следует принять многочлен P(x) .

Для интегралов вида , ,

за u(x) принимаются функции lnx, arcsinx, arctgx, а за dv - выражение P(x)dx .

_Т.е.

Доказательство.

Пусть F₁(x) и F₂(x) соответственно некоторые первообразные для   и  .

Тогда по определению первообразной и правилу дифференцирования произведения двух функций  + = ,  .

Следовательно, по следствию из теоремы Лагранжа:

F₁(x) + F₂(x) =  + c, где c – некоторая константа, или F₁(x) =  - F₂(x).

Так как

 

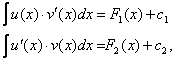
из данного равенства следует, что 

Замечание: Формулу интегрирования по частям следует понимать так: множество функций {F₁(x) + C₁}, стоящих в левой части равенства, совпадает со множеством функций { -F₂(x) + c₃}, стоящих в правой части, где с₃ = с – с₂, а с₁ и с₂ – произвольные числа.