16.Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

  Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

 Для нахождения суммарной площади используется формула .

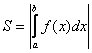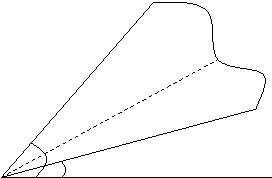
 Нахождение площади криволинейного сектора.

 

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид  = f(), где  - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а  - угол наклона этого радиус – вектора к полярной оси. Площадь криволинейного сектора может быть найдена по формуле

  

Вычисление длины дуги кривой.

 Длина ломаной линии, которая соответствует дуге, может быть найдена как .

Тогда длина дуги равна .

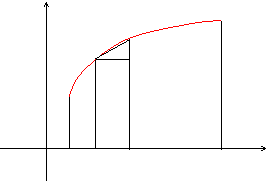
Из геометрических соображений:

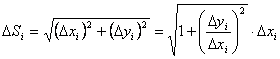
  Если задана пространственная кривая, и х = (t), у = (t) и z = Z(t), то

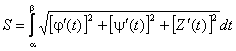
  Если кривая задана в полярных координатах, то

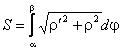,  = f().

17.Несобственные интегралы по бесконечному промежутку интегрирования от непрерывных функций.

Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при называется несобственным интегралом функции f(x) от a до и обозначается . Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.

Пусть на полуинтервале задана функция , интегрируемая на любом отрезке, принадлежащем данному интервалу, однако не интегрируемая на отрезке . В точке эта функция может быть вовсе не определена и стремиться к , либо вовсе не иметь никакого предела. Рассмотрим функцию . Она определена при . Эта функция может иметь предел при (левосторонний предел). Этот предел будем называть значением интеграла от по всему полуинтервалу и обозначать в точности: Определение. Пусть функция удовлетворяет указанным выше условиям на . Несобственным интегралом второго рода назовём определенный интеграл

значение которого равняется левостороннему пределу

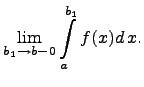
Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения.

19.Дифференциальные уравнения.

Уравнение, в которое входят производные неизвестной функции, называется дифференциальным. Если эта искомая функция зависит лишь от одного аргумента то наз обыкновенным дифф. уравнением. Если же неизвестная функция является функцией нескольких независимых переменных, то диф уравнение называется уравнением в частных производных.

Порядком диф ур-я наз макс порядок входящей в него производной неизвестной ф-и.

Решением диф ур-я наз любая ф-я, при подстановке которой в ур-е (с учётом входящих в него производных) получится тождество.

Общее решение диф ур-ия — функция наиболее общего вида, которая при подстановке в диф ур-ие вида обращает его в тождество.

Частным решением диф ур-ия на интервале называется каждая функция , которая при подстановке в уравнение вида

обращает его в верное тождество на интервале .

Всякое решение диф ур-я при условии у(х₀) = у₀, (1.5) где х₀ – произвольная точка из промежутка, на котором рассматривается уравнение, а у₀ – произвольно заданное число, называется частным решением (частным интегралом) диф уравнения. График частного решения называют интегральной кривой. Геометрически оно означает, что на плоскости Оху задаётся точка М₀(х₀, у₀), через которую должна проходить искомая интегральная кривая, т.е. график функции у = у(х). Задача нахождения решения диф ур-я или с присоед к нему условием (1.5), называется задачей Коши или задачей с начальным условием.