Лінійне і нелінійне програмування

7.1. Лінійне програмування

Оскільки в економічних сферах діяльності при оптимізації використання обмежених ресурсів метод лінійного програмування застосовують доволі часто, є сенс висвітлити деякі прикладні аспекти, що з цим пов’язані. Найчастіше метод лінійного програмування (ЛП) можна зустріти при вирішенні питань оптимізації номенклатури продукції (які продукти випускати), що виробляти при умові обмежених потужностей, при вирішенні проблем постачання, зокрема, оптимізації витрат на транспортні перевезення, як обрати постачальника, як розмістити виробництво, управління чергою і проектом, на яку діяльність орієнтуватись фірмі - виробляти чи купувати. Щодо вимог до параметрів зв’язків об’єкту, як системи, то у разі використання методу ЛП вони повинні бути лінійні. Тобто, потрібно знайти таку комбінацію випуску продукції, оперативних дій при яких визначений параметр, сягатиме максимальних, або мінімальних значень.

Розглянемо формальну сутність такого класу задач на прикладі спрощенної ситуації.

Хай є різні види сировини (ресурсів) у кількості b₁, b₂,…, b_m із яких може бути виготовлено n видів продукції. Якщо означити через х_j – довільну кількість j-го продукту, через а_ij– витрати і-го ресурсу на отримання одиниці j-го виду продукції, а через с_j – ціну одиниці j-ї продукції можна прийти до такої екстремальної задачі: знайти при умовах, що сумарні витрати сировини (ресурсів) не повинні перевищувати ті які маються - і що кількість продукції яка виробляється не може бути від’ємною – х_j > 0, j = 1,2,…, n. Будь-який набір значень х₁, х₂, …, х_n , що задовольняє означеним умовам звуть припустимим планом. Так може бути описана проста ситуація із лінійними обмеженнями і функцією мети.

Сутність таких задач добре ілюструється у разі їх геометричної інтерпретації.

Хай маємо декартову систему координат – Х₁ОХ₂ (рис.7. 1), де кожне із обмежень геометрично визначає множинність точок, що розташовані із одного боку прямої.

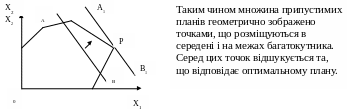
Рисунок 7.1 Графічне зображення процедур пошуку оптимального рішення

Якщо задатися числом, щоб пряма с₁х₁+с₂х₂ = а перетинала багатокутник припустимих планів і почати переміщувати її паралельно самій себе у бік зростання а доки пряма не співпаде із однією із верхівок або сторін багатокутника, то буде досягнуто цільову функцію (Р). Однак у разі значень n > 2 труднощі, що пов’язані з таким підходом до вирішення задачі значно зростають. Така перешкода усувається введенням об’єктивно обумовлених оцінок (ООО) використання кожного виду ресурсів (сировини), які надають змогу оцінити його економічну корисність. Особливістю цих оцінок є те, що вони є також і рішенням деякої задачі лінійного програмування – двоїстої задачі.

Побудуємо таку задачу до розглянутої раніше. Тобто наша турбота буде полягати не в тім, щоб отримати більше, а в тому, щоб менше витратити. Введемо оцінки у₁, у₂, …, у_n для всіх видів сировини і мінімізуємо функцію - оцінка сировини. Значення у_i повинні бути позитивними і бути меншими за оцінку одиниці продукту. Тобто потрібно знайти при умовах: у_і > 0, і = 1,2,…, m ; . Підкреслимо, що основна і двоїста задачі лінійного програмування мають математичні властивості які роблять доцільним їх сумісне розглядання. Якщо одна із пари двоїстих задач має рішення, то інша задача теж вирішується. При цьому для будь-яких оптимальних планів цих задач справедливим є співвідношення: . Змістовно це означає, що оптимальний план виробництва існує, якщо можна визначити оптимальний план оцінок. Тобто, особливість оптимального плану полягає в тому, що для такого плану співпадатимуть оцінки витрат і оцінки результатів виробництва.

Формально метод реалізується через розбудову системи рівнянь. Як вже було відмічено, при наявності в системі двох змінних (ресурси розподілені між двома товарами) рішення можна отримати графічними засобами. Якщо змінних більше – знадобиться спеціальний інструментарій.

Приклад 7.1.1

Розглянемо вже відому нам задачу коли компанія випускає товари А і В, технології виробництва кожного із них складаються з трьох етапів. Пипустимо, що менеджер для прийняття рішення щодо об’ємів випуску товарів А і В має у своєму розпорядженні таку інформацію (табл..7.1):

Таблиця 7.1. Вхідні дані задачі

Продукти	Етапи			Дохід	Попит
	х	у	z
А	3	2	4,5	140	10
В	4	1	3,5	100	18
Потужність	60	30	70

Слід визначити:

1. Тривалість стадій технологічного процесу виготовлення продукції;

2. Об’єм виробничих потужностей (годин/тиждень);

3. Дохід від кожного із видів продукції;

4. Попит (одиниць/тиждень).

Числовий запис умов задачі:

Цільова функція: 140А+100В max.

Обмеження:

Стадія х - 3A + 4B  60

Стадія у - 2A + B  30

Стадія z - 4,5А + 3,5B  70

Попит на продукцію А: 0  А  10

Попит на продукцію В: 0  В  18.

Задача може бути вирішена графічно в ручному режимі і у комп’ютерному варіанті.

Графічний варіант рішення задачі методом лінійного програмування

Запишемо умови у символьному забраженні і у нашому випадку матимемо цільову функцію F(х₁, х₂) = С₁х₁+С₂х₂ → max і три функціональні обмеження: a₁₁x₁+a₁₂x₂ ≤ b₁; (1).

a₂₁x₁+a₂₂x₂ ≤ b₂ ;(2).

a₃₁x₁+a₃₂x₂ ≤ b₃; (3)

x₁≥0; x₂≥

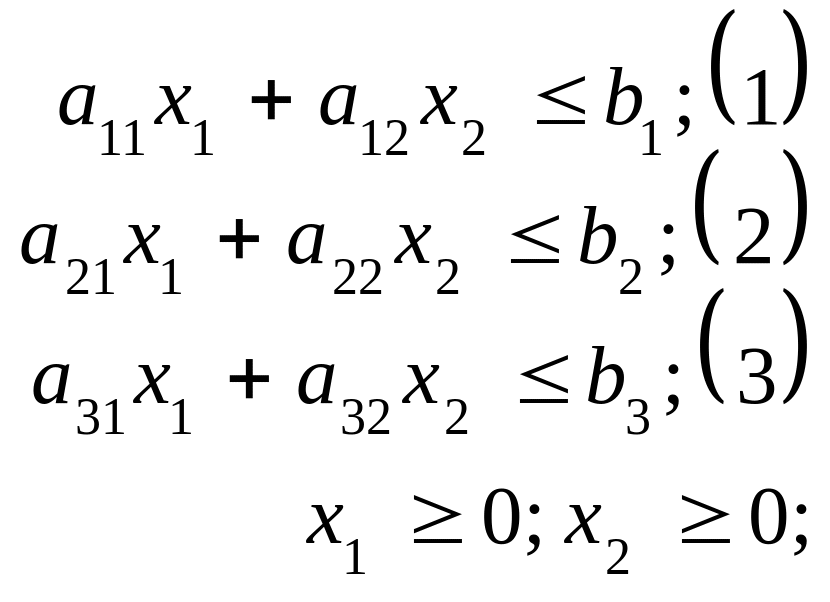
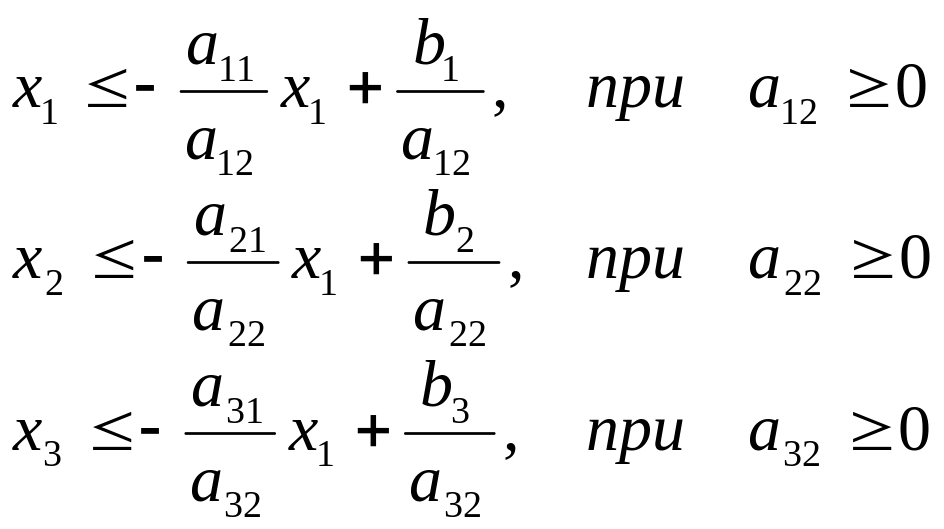Накреслимо на площині осі координат Х₁ і Х₂ (рис.7.2); у цих осях побудуємо графіки для обмежень; накреслимо графік цільової функції для випадку коли вона приймає фіксоване значення Z₁ (у разі зростання Z графік цільової функції зміщується догори-праворуч):

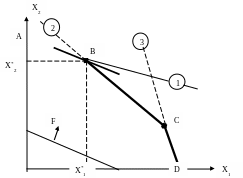
Рисунок 7.2. Графічне рішення задачі лінійного програмування (номери ліній відповідні до номерів нерівностей).

Хай де: Z₁ - будь-яке число. Виразимо х₂ і отримаємо, що Хай С₁х₁+ С₂х₂ = Z > Z_1. . Для того щоб зростало значення цільової функції потрібно пряму зміщувати в напрямку, що вказує стріkка (рис.7.2). Максимум буде у якійсь з вершин опуклого багатокутника, тобто будуть задовольнятися обмеження і буде досягатись екстримум цільової функції. Оптимальним рішенням у даному випадку будуть значення х₁^* і х^*₂. Для нашого графіку оптимальне рішення єдине.

На рисунку вказані номери обмежень, пунктиром – цільова функція при деякому Z, суцільна лінія – положення при якому значення цільової функції максимальне, х^*₁ і х^*₂ – ті значення змінних, при яких досягається максимум цільової функції. В результаті оптимальний дохід у точці z буде при умові випуску типів товарів у об’ємах: А = 9, В = 8 і А = 10, В = 7 одиниць. Можно підрахувати, що у першому випадку дохід становитиме 2060, у другому – 2100 грн. Тобто варіант z вважатиметься переважним.

Приклад 7.1.2 ( Комп’ютерний варіант)

Фірма виробляє товари трьох модифікацій - М-І, М-ІІ, М-ІІІ (n >2). Максимальні тижневі витрати, що пов’язані із роботами по виробництву комплектуючих, по збиранню і тестуванню, пакуванню складають відповідно 3600, 2400, 1800 грн. Прибуток від реалізації одного комплексного виробу модифікацій І, ІІ, ІІІ відповідно – 15, 22 ,19 грн.

Спираючись на дані таблиці 7.2 менеджеру потрібно вирішити такі проблеми:

1. Визначити оптимальний план випуску на тиждень;

2. Максимізувати прибуток;

3. Як зміняться умови випуску якщо фірма має котракт на постачання у продовж тижня не менще ніж 30 виробів типу М - ІІІ. До того ж, слід враховувати, що можливості зберігання виробів обмежені у розмірі 140 одиниць.

Таблиця 7.2. Ісходні дані задачі

Операції	Витрати на операції по типам виробів			Загальні витрати
	І	ІІ	ІІІ
Виготовлення комплектуючих	20	10	10	3600
Збирання виробу і тестування	30	20	10	2400
Пакування	20	30	20	1800

Ррішення:

Х_1, Х₂, Х₃ – кількість виробів модифікацій М-І, М-ІІ, М-ІІІ

Цільова функція:

Обмеження:

; ;

Х_1, Х₂, Х₃ – цілі числа.

Технологія рішення:

Значення клітинки А8 відшукується із використанням встроєної функції СУММПРОИЗВ (1-й масив; 2-й масив) , де 1-й масив складають значення прибутку від реалізації кожного виробу модифікацій І, ІІ, ІІІ (діапазон клітинок Н2:Н4); 2-й масив формується із значень змінних Х₁ Х₂ Х₃ (діапазон В2:В4). В такому разі у клітинці А8 буде міститись формула: =СУММПРОИЗВ (Н2:Н4;В2:В4). У діапазон клітинок С8:Е8 вводяться ліві частини нерівностей обмежень. Так у клітинку С8 вводиться формула = СУММПРОИЗВ (С2:С4; $B$2:$B$4). Для випадків модифікацій ІІ і ІІІ цю формулу слід скопіювати в клітинки Д8:Е8, використавши маркер заповнення.

Таблиця 7.3. Робоча матриця задачі

	A	B	C	D	E	F	Q	H
1		Значення	І	ІІ	Ш			Прибуток
2	Х1	0	20	10	10			15
3	Х2	0	30	20	10			22
4	Х3	0	20	30	20			19
5			3600	2400	1800
6
7	Цільова функція		1-а умова	2-а умова	3-я умова
8	0		0	0	0

Опісля заповнення робочої матриці підключається функціяі "Оптимізатора": Сервис → Поиск решения(рис.7.3).

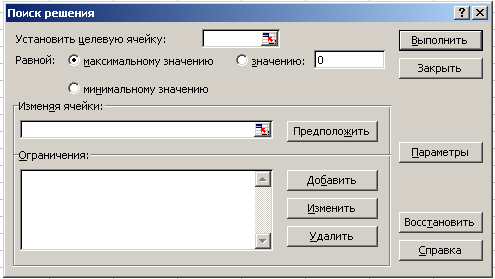
Рисунок 7.3 Фрагмент інтерфейсу „Оптимізатора”

У діалогове вікно включаємо адреса комірки цільової функції; Для обмежень – Добавить (з’являється діалогове вікно) заповнити посиланнями на відповідні комірки робочої матриці ( на комірки і обмеження, що накладаються на змінні).

Рисунок 7.4 Перетворення робочої матриці у підсумкову таблицю

Після отримання результатів рішення до системи обмежень додаємо обмеження стосовно контрактних забов’язань фірми стосовно М- ІІІ .

Вводимо додаткове обмеження - Х₃ ≥ 30. Система рівнянь буде мати вигляд:

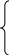
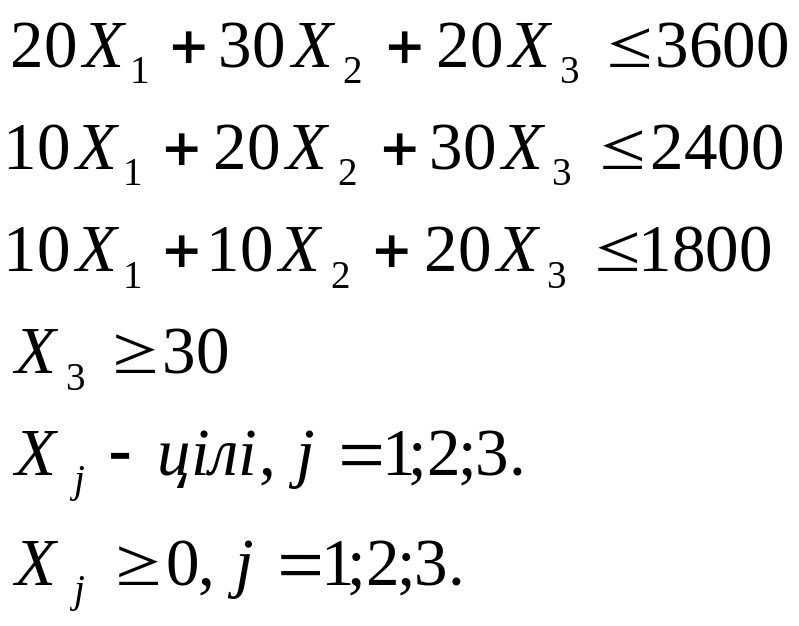
Рисунок 7.4а . Результат рішення при умові додаткового обмеження

У діалоговому вікні "Оптимізатора" додається нове обмеження - $F$8 =$F$5 [у комірці F8-CУММПРОИЗВ( В2:В4; F2:F4), а у комірці F5 –30] – (табл. 7.4). В такому випадку фірмі вигідно виробити М-І, М-ІІ, М-ІІІ у кількості 90, 30, 30 одиниць відповідно, щоб отримати прибуток у 2580 грн (рис.7.4а).

Вводимо умови – обмеження щодо збереження виробів (140 одиниць) -Х₁+Х₂+Х₃ 140

У діалоговому вікні надбудови «Поиск решений» знову додаємо нове обмеження. На цей раз фірма отримує прибуток 2500 грн і зміну у номенклатурі виробів (рис. 7.4b).

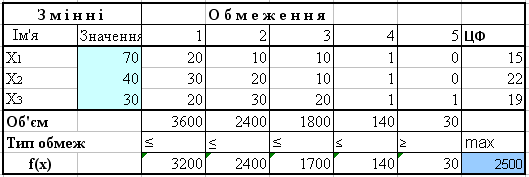
Рисунок 7.4 b. Результат рішення при додатковому обмеженні

Приклад 7.1.3

Бензин А-76 має октанове число не нижче за 76, сірки містить не більше ніж 0,31%. Фірма має необхідні компоненти для виготовлення якісного палива (табл.7.4).

Таблиця 7.4. Ісходні дані задачі

Показники	Компоненти
	1	2	3	4
Октанове число	68	72	80	90
Вміст сірки, %	0,35	0,35	0,3	0,2
Об’єм складових, т	700	600	500	300
Собівартість,	40	45	60	90

Визначити скільки і яких компонентів треба, щоб отримати 1000 т палива марки А-76 із мінімальною собівартістю. Сформуємо сутність задачі у вигляді системи рівнянь і робочої матриці (табл. 7.5).

Змінні: Х_1, Х₂, Х₃, Х₄ – оптимальна співвідношення компонентів.

Функція мети: f(х) = 40 Х₁+45Х₂+60Х₃+90Х₄ → min

Ообмеження:

- за октановим числом: 68Х₁+72Х₂+80Х₃+90Х₄ ≥ 76 ^. 1000

- за вмістом сірки: 0,35Х₁+0,35Х₂+0,3Х₃+0,2Х₄ ≤ 0,3 ^. 1000

- за об’ємом готової продукції: Х₁+Х₂+Х₃+Х₄ = 1000

- за ресурсами складових: Х₁≤700, Х₂ ≤ 600 , Х₃ ≤500, Х₄ ≤300;

- позитивність змінних: Х_{1 ,} Х₂, Х₃, Х₄ ≥ 0

Рішення дає: Х = (571; 0; 143; 286; 0; 0; 129; 600; 357). Використовувати суміш, що складається з 571 т. компонента 1; 143 т компонента 3 і 286 т компонента 4. Мінімальна собівартість всього об’єму А-76 становитиме 57143 грн.(табл.7.5).

Таблиця 7.5. Робоча матриця задачі

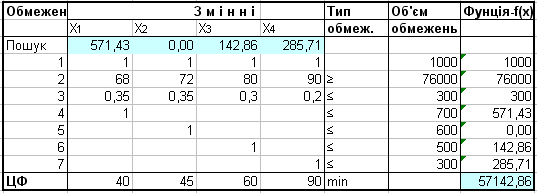
Приклад 7.1..

Хай підприємство має намір виготовити стоп металу із таких компонентів: олова – 15%, цинку - 55% і свинцю - 30%. Які стопи використовувати і у яких об’ємах, щоб сумарні витрати були мінімальні?

Таблиця 7.6. Ісходні дані задачі

Показники	Стопи
	1	2	3	4	5
Вміст свинцю, %	40	30	25	15	35
Вміст цинку, %	40	60	45	15	60
Вміст олова, %	20	10	30	20	5
Вартість одиниці стопу, грн.	5	4	7	5	3

Запишемо умови у числовому виразі:

Критеріальна функція:

Обмеження:

Х₁+Х₂+Х₃+Х₄+Х₅ = 1

40Х₁+30Х₂+25Х₃+15Х₄+35Х₅ = 30

40Х₁+60Х₂+45Х₃+65Х₄+60Х₅ = 55

20Х₁+10Х₂+30Х₃+20Х₄+5Х₅ = 15

Х₁>0; Х₂>0; Х₃>0; Х₄>0; Х₅>0.

Рішення: Застосовуємо вже відому опцію „Поиск решений” і отримуємо результат:

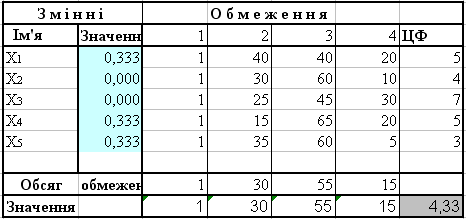
Рисунок 7.5 Результат рішення задачі

Оптимізація структури посівних площь

Приклад 7.1.5

Корпорація має 2000 га орної землі. Ресурси праці складають 300000 люд.-годин, грошові ресурси – 1500000 грн. Контрактні зобов’язання на зерно – 16000 цнт. Найбільш придатними культурами вважаються зернові, картопля і кормові коренеплоди. Планується, що частина зерна буде використана як фуражне в обмін на комбіновані корми. При цьому потреба у комбікормах складає 66737 корм.одиниць.

Визначити яку площу повинні зайняти кожна із культур, щоб прибуток був максимальним.

Таблиця 7.7. Робоча матриця (нормативна інформація)

Вид ресурсів	Зерно товарне - Х1	Зернові в обмін на комбікорми - Х2	Картопля - Х3	Коренепло- ди - Х4
Витрати люд.-годин на 1га	20	20	300	500
Грошові витрати на 1га	250	250	1500	1000
Вихід кормів на 1га, ц. корм. од.	-	40	-	75
Прибуток з 1 га	100	-	500	-

Обмеження:

-На ресурс землі;

- На використання ресурсів праці;

-На використання грошових ресурсів; млн.

- На придбання комбікормів:

- На виробництво товарного зерна:

Цільова функція:

Задача вирішується за допомогою "Оптимізатора".

Результати рішення:

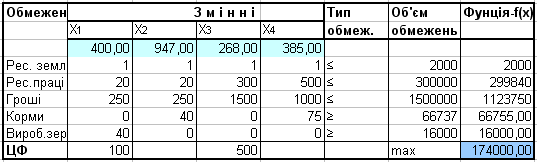
Х₁ = 400 га (зерно товарне)

Х₂ = 947га (зерно в обмін на комбікорми)

Х₃ = 268 га (картопля)

Х₄ = 385 га (коренеплоди). Прибуток - 174000 грн..

Рисунок 7.6 Функціональні складові „Оптимізатора”

Таблиця 7.8. результати рішення задачі

7.1.1. Аналіз оптимального рішення. Теорема двоїстості

Хай підприємство має бажання і потужності для виробництва чотирьох типів продукції і використовує при цьому три види матеріалів.

Вхідна інформація наведена в таблиці 7.9.

Таблиця 7.9 Вхідна інформація

Вид продукції	Норма витрат матеріалів на одиницю продукції			Прибуток від реалізації оди-ниці продукції
	1	2	3
А	7	5	2	3
Б	2	8	4	4
В	2	4	1	3
Г	6	3	8	1
Ресурси	80	480	130	-

Службі маркетингу необхідно перевірити, чи буде оптимальним у цих умовах план випуску 30 одиниць продукції Б и 10 одиниць продукції В (продукція видів А и Г не випускається) за критерієм максимізації прибутку, що отримується. Крім того, треба визначити ступінь дефіцитності матеріалів, що використовуються і ступінь впливу на показник цільової функції змінення об’ємів ресурсів, передбачається у таких вимірах: збільшення ресурсу матеріалу 1 на 3 одиниці, зменьшення ресурсу матеріалу 3 на 6 одиниць.

А). Формування економіко-математичної моделі.

Змінні: Х₁, Х₂, Х₃, Х₄ – кількість продукції кожного виду. Цільова функція:

Обмеження:

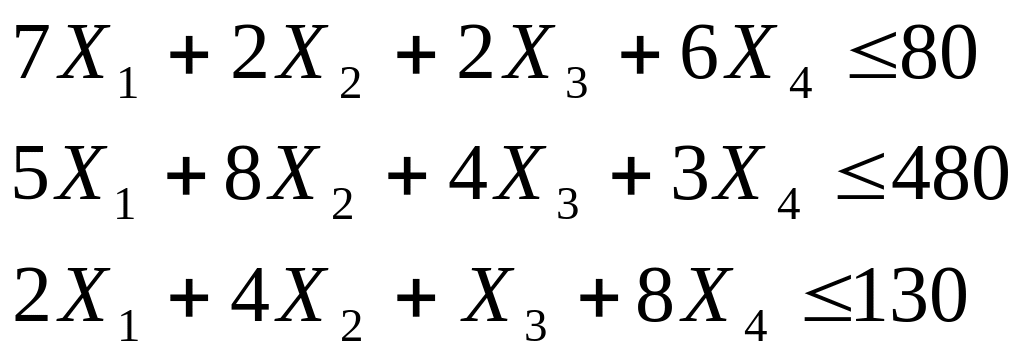
Таблиця 7.10. Оптимальний план випуску

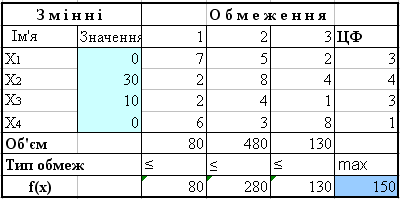
Запропонований для анализу план: Х₁ = 0; Х₂ = 30; Х₃ = 10; Х₄ = 0 є припустимим рішенням. При цьому ресурси матеріалу 1 і матеріалу 3 використані сповна, а витрати матеріалу 2 складають 280 одиниць. Тобто залишається злишкова частина цього матеріалу у кількості 480 – 280 = 200 одиниць. Для такого плану прибуток становитиме: грн.

Б). Формуємо подвійну задачу по відношенню до початковій змінній: У₁, У₂, У₃ – двоїсті оцінки 3-х видів матеріалів. Скористаємось відношенням: ; . Складаємо систему рівнянь: а) цільова функція - ;b) система обмежень:

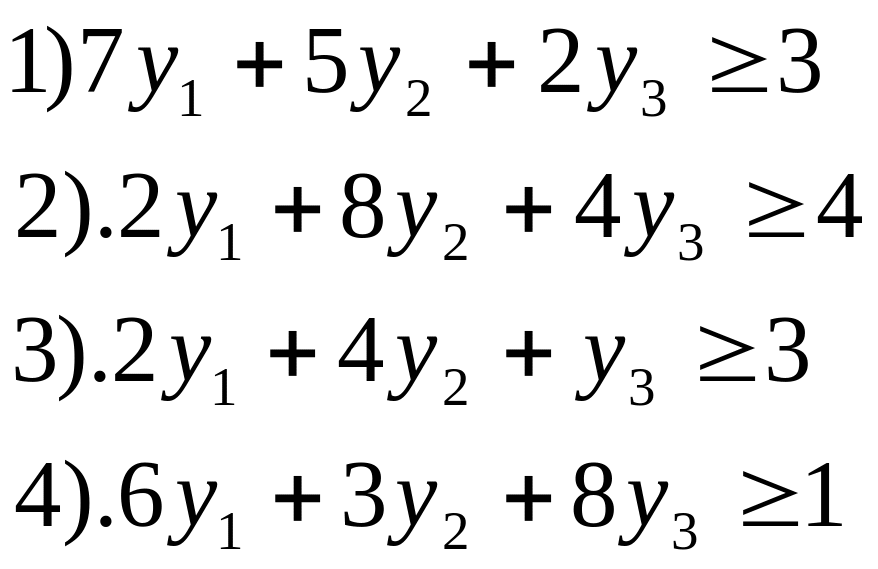
5). У₁, У₂, У₃ 0

Таблиця 7.11. Результати вирішення двоїстої задачі

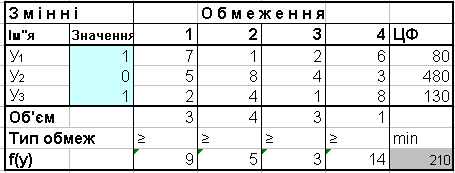
Із перших співвідношень (за кількістю видів продукції їх чотири) витікає, що оскільки Х₂ = 30; Х₃ = 10, то відповідні друге і третє функціональні обмеження двоїстої задачі перетворюються у рівняння:

2У₁+8У₂+4У₃ = 4; 2У₁+4У₂+У₃ = 3

Із інших співвідношень (за кількістю видів матеріалів їх три ) витікає, що оскільки матеріал 2 витрачається нерівністю (280 – 480 = -200), то його відповідна двоїста оцінка дорівнює 0 (У₂ = 0). Якщо підставити це значення у наведене рівняння і вирішити систему двох рівнянь відносно У₁ і У₂, будемо мати: У₁ = 4/3; У₃ = 1/3. Для знайдених значень змінних двоїстої задачі розрахуємо значення цільової функції цієї задачі:

Співставляючи значення цільової функції обох задач, бачимо, що для варіанту виробничого плану який розглядається - , тобто, із першої теореми двоїстості цей варіант є оптимальний і дає максимальний прибуток = 150. Відповідно до цього значення змінних двоїстої задачі є об’єктивно обумовленими оцінками 3-х видів матеріалів і на підставі цього можна зробити висновок про ступінь дефіцитності матеріалів. Матеріал 2 є не дефіцитним, (у₂ = 0), а матеріал 1 і 3 є дефіцитними (У₁ = 4/3; У₃ = 1/3), при цьому більш дефіцитним буде матеріал 1.

Також ми отримали відповідь і на останнє завдання у задачі. Скористаємось висновком із третьої теореми двоїстості щодо існуючих ресурсів матеріалів які знаходяться у межах інтервалу сталості оптимального рішення і на підставі співвідношення визначимо: .

Тобто, дані зміни об’ємів ресурсів приведуть до збільшення максимального прибутку на 2 одиниці і у кінцевому підсумку прибуток становитиме 152 одиниці.