Итерационный метод с чебышёвским набором параметров

Пусть рассматривается система линейных алгебраических уравнений Ax = f с симметричной положительно определенной матрицей А. Решение будем искать с помощью явного нестационарного метода Ричардсона,

Попытаемся так определить набор , чтобы была минимальной для заданного числа итераций N.

Теорема 2.6. Пусть А - симметричная положительно определенная матрица, - наименьшее и наибольшее собственные значения. Пусть задано число итераций N. Среди всех наборов , наименьшую погрешность имеет набор, для которого

Оценка погрешности в этом случае имеет вид:

.

Доказательство. Введем, как и ранее, погрешность решения . Схема Ричардсона позволяет записать систему уравнений относительно погрешностей:

.

Отсюда получаем

.

В частности,

,

. . .

.

Обозначим

.

Понятно, что - симметричная матрица. Теперь погрешность на N итерации можно представить выражением

.

Для симметричной положительно определенной матрицы в качестве нормы может быть выбран спектральный радиус . В самом деле, для собственного вектора , соответствующего собственному значению ,

,

.

С учетом свойств нормы получаем

(2.19)

С другой стороны, пусть - ортонормированная система векторов, построенная на основе собственных векторов матрицы ,

.

Разложим вектор  по этому базису:

.

Согласно определению нормы вектора

В компонентной записи вектор с использованием собственных чисел и векторов выглядит следующим образом:

.

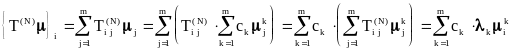Здесь использовано определение собственных значений и векторов:

.

Учитывая, что

,

можно подсчитать норму оператора

.

Сравнивая последнее неравенство с выражением (2.19), определяем точное значение нормы:

.

С учетом этого можно оценить величину погрешности:

.

Построение доказательства теоремы 2.6 основано на поиске такого набора , который минимизирует спектральный радиус  матрицы .

Предположим, что все собственные значения матрицы А упорядочены:

.

Известно [7], что если f(A) - матричная функция матричного аргумента А, то - полная система собственных значений матрицы f(A).

Поскольку

является как раз матричной функцией матричного аргумента, то соответствующая скалярная функция

определяет собственные значения матрицы . В этом случае ее спектральный радиус может быть определен как

.

Обозначим

. (2.20)

Тогда спектральный радиус можно определить следующим образом:

и определение набора сводится к задаче поиска

.

Очевидно, что функция (2.20) является полиномом степени N, причем f(0) = 1. Иначе говоря, поиск итерационных параметров сводится к задаче об отыскании полинома степени N, наименее уклоняющегося от нуля на отрезке , которая может быть решена с использованием полинома Чебышёва.

Корни функции (2.20) принимают значения:

и должны совпадать с корнями полинома Чебышёва:

.

Теперь очевидно, что итерационные параметры следует выбирать следующим образом:

.

Обозначения соответствуют введенным при формулировке теоремы.

Для оценки нормы погрешности заметим, что

,

откуда получаем .

Что и требовалось доказать.