Формула трапеций

Заменим функцию f(x) на отрезке линейным приближением

.

Это означает, что в разложении (7.2) удерживаются две функции .

Тогда весовые коэффициенты

Отсюда вытекает формула метода трапеций (рис. 7.4):

. (7.8)

Воспользуемся формулами Тейлора

,

.

x_k-1 x_k x

Рис. 7.4. Схема численного интегрирования методом трапеций

Оценим погрешность представления (7.8) на отрезке :

В силу того, что

,

,

вычисляемая погрешность

.

Получим оценку погрешности:

.

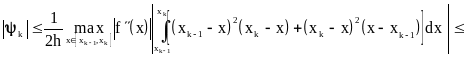
Погрешность для всего отрезка интегрирования [a, b]

(7.9)

имеет второй порядок.

На рис. 7.5 показан график сходимости приближенного значения определенного интеграла , полученного с помощью формул метода трапеций.

Рис. 7.5. Значения интеграла , вычисленные точно ( ------ ) и по формуле метода трапеций ( -  - ) на сетках _n

Формула Симпсона1

Заменим на отрезке функцию f(x) полиномом Лагранжа. В частности, для трех точек полином второй степени имеет вид

Это означает, что в разложении (7.2) оставлены три функции:

,

,

.

Для определения коэффициентов вычислим интегралы:

.

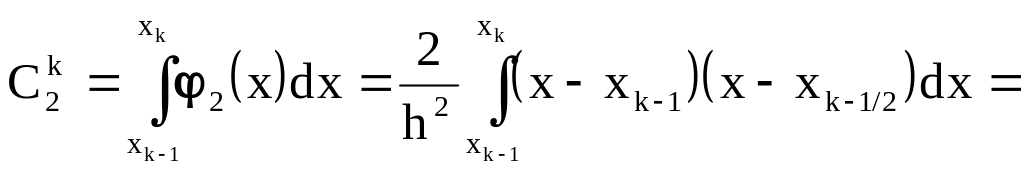
Формула приближенного интегрирования Симпсона (рис. 7.4):

. (7.10)

f(x)

x_k-1 x_k-1/2 x_k x

Рис. 7.6. Схема численного интегрирования методом Симпсона

Для оценки погрешности выражения (7.10) приближенного интегрирования, как и ранее, воспользуемся формулами Тейлора для представления вблизи точки :

,

,

Здесь принято, что .

Подсчитаем интеграл в левой части формулы (7.10):

.

Подсчитаем выражение в правой части (7.10):

.

Определим величину погрешности формулы Симпсона:

.

Модуль погрешности на отрезке :

.

Для всего отрезка [a, b] интегрирования погрешность

(7.11)

имеет четвертый порядок.

В последних выражениях использованы обозначения

, .

На рис. 7.7 изображен график сходимости приближенного значения определенного интеграла , полученного с помощью формул метода Симпсона.

Рис. 7.7. Значения интеграла , вычисленные точно ( -------- ) и по формуле метода Симпсона ( - o - ) на сетках W_n

Формула Эйлера1

При исследовании численного интегрирования методом трапеций получена формула для вычисления погрешности на отрезке :

.

Положим , то есть равными координате в середине указанного отрезка. Тогда может быть приближенно вычислена величина погрешности интегрирования:

(7.12)

Учитывая, что

,

получим уточненную формулу интегрирования

.

Вспоминая, что согласно теореме Лагранжа , получим формулу интегрирования Эйлера:

. (7.13)

Погрешность формулы (7.13) на отрезке [a, b] оценивается формулой, совпадающей с выражением (7.11).