Машинная реализация вычислений

Рассмотрим задачу об оценке погрешности вычисления произведения . В соответствии с определением относительной погрешности приближенное значение переменной можно представить в виде . Приближенный (округленный) результат произведения двух первых чисел в указанном выражении может быть оценен формулой . Очевидно, что для получения значения всего выражения следует многократно повторить эту операцию:

.

Для получаем , что соответствует величине относительной погрешности вычисления всего результата 0,0998501 % . При перемножении 1 000 000 сомножителей погрешность может достигнуть 63,212 % . На практике такого катастрофического нарастания погрешности, как правило, не наблюдается в силу того, что погрешности округления могут иметь разные знаки и зачастую компенсируют друг друга.

Контрольные вопросы и задания

• Дайте определение понятиям “математическая модель”, “вычислительный эксперимент”, “алгоритм”, “компьютерное моделирование”.

• Опишите этапы выполнения вычислительного эксперимента.

• Укажите причины погрешностей математической модели. Какие из них являются неустранимыми, а какие - регулируемыми?

• Объясните причины погрешности исходных данных.

• Что понимается под погрешностью численного метода?

• Как оценить величину погрешности вычислений на ЭВМ?

• Какую погрешность, относительную или абсолютную, целесообразно оценивать и почему?

2. Системы линейных алгебраических уравнений

Система m линейных алгебраических уравнений представляется в виде

Ax = f, (2.1)

где A - квадратная матрица ранга m;

- правая часть системы уравнений; - искомый вектор.

Система уравнений (2.1) имеет единственное решение, если определитель det(A) отличен от нуля. В развернутой (компонентной) записи эта система уравнений имеет вид

(2.2)

Прямые методы решения

Прямыми называют методы решения систем линейных алгебраических уравнений, для которых результат получается за конечное, заранее определенное, число арифметических операций. Наиболее популярным среди них является метод Гаусса¹.

Метод Гаусса

Рассмотрим процедуру решения системы линейных алгебраических уравнений методом Гаусса на следующем примере:

Главный определитель такой системы

,

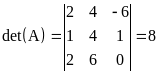что гарантирует единственность решения.

1 шаг. Первая строка системы уравнений делится на первый коэффициент:

2 шаг. Первая строка вычитается из второго уравнения:

3 шаг. Из третьего уравнения вычитается первая строка, умноженная на 2:

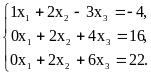
4 шаг. Второе уравнение делится на 2:

5 шаг. Из третьего уравнения вычитается второе уравнение, умноженное на 2:

6 шаг. Определяются искомые величины:

Таким образом, получено решение исходной системы уравнений.

Теперь рассмотрим процедуру получения решения методом Гаусса в более общем случае. Пусть . Тогда первое уравнение системы (2.2) можно поделить на этот коэффициент:

.

С помощью этого уравнения можно преобразовать систему уравнений (2.2) к виду

Здесь обозначено . В полученной системе можно выделить подсистему (m-1) линейных уравнений с (m-1) неизвестными величинами:

Пусть теперь . Поделим второе уравнение системы на этот коэффициент:

.

С помощью этого соотношения уравнения системы преобразуются к виду

Здесь обозначено .

В результате преобразований получена подсистема (m-2) уравнений с (m-2) неизвестными:

В предположении, что , делим третье уравнение системы на этот коэффициент:

.

Снова выполняется следующий шаг по понижению порядка системы алгебраических уравнений, и так далее, до тех пор, пока вся система уравнений не будет преобразована к виду

В результате всех произведенных выкладок матрица коэффициентов А системы алгебраических уравнений приведена к виду

- “верхняя” треугольная матрица¹, у которой равны нулю все элементы, расположенные под главной диагональю. Процедура получения такой матрицы носит название “прямого хода” метода Гаусса. Очевидным условием для успешного выполнения “прямого хода” является .

“Обратный ход” метода позволяет определить искомые величины:

Таким образом, “прямой ход” метода Гаусса можно трактовать как преобразование системы уравнений вида Ax = f в эквивалентную систему Ux = y, причем

.

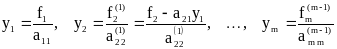Последнюю систему соотношений с учетом вышеприведенных выкладок можно представить в иной форме

и записать в виде Ly = f , где L - нижняя треугольная матрица¹ с отличными от нуля коэффициентами на главной диагонали.

Все вышесказанное позволяет трактовать метод Гаусса как последовательное решение двух систем уравнений: Ly = f и Ux = y .

Объединяя эти соотношения, получаем

LUx = f.

Сравнивая последнюю формулу с записью уравнения (2.1), можно сделать заключение, что процедура метода Гаусса эквивалентна разложению исходной матрицы коэффициентов в произведение двух матриц специального вида:

L - нижняя треугольная матрица с ненулевыми коэффициентами на главной диагонали;

U - верхняя треугольная матрица с единицами на главной диагонали.

Обозначим угловые миноры матрицы А символами :

Теорема 2.1. Пусть все угловые миноры матрицы А отличны от нуля, . Тогда матрицу А можно представить единственным образом в виде

A = LU, (2.3)

где L - нижняя треугольная матрица с ненулевыми диагональными элементами, U - верхняя треугольная матрица с единицами на главной диагонали.

Доказательство теоремы проводится по индукции.

Рассмотрим разложение матрицы для простейшего случая m=2. Пусть в этом случае матрицы имеют вид

Предполагая разложимость для m=2, получаем систему уравнений относительно коэффициентов матриц L₂ и U₂ :

Решение этой системы уравнений дает значения коэффициентов:

Это означает, что возможность разложения (2.3), соответствующего условию теоремы, показана для простейшего случая m=2. Теперь предположим, что условия теоремы выполнены для случая (m-1), то есть имеет место разложение . Вводя обозначения

представим матрицы в форме

Здесь принято, что

.

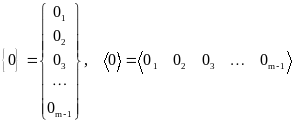Покажем существование разложения для матрицы . Перемножая и сравнивая результат со структурой матрицы , получаем систему (2m-1) алгебраических уравнений относительно (2m-1) неизвестного :

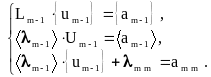
В силу того, что (треугольные матрицы с ненулевыми значениями на главных диагоналях), существуют единственные решения первых двух систем уравнений: . И, кроме того, может быть вычислено последнее неизвестное , значение которого должно быть отлично от нуля. Для того, чтобы убедиться в этом, произведем следующие выкладки:

.

В силу того, что , имеет место равенство , из которого сразу следует, что . При выполнении последних преобразований вновь учтено, что матрицы являются диагональными, а их определители представлены разложениями соответственно по последнему столбцу и нижней строке.

Покажем единственность разложения (2.3). Предположим, что такое разложение возможно не единственным образом, то есть

.

Проводя простейшие преобразования, получаем

Можно заметить, что поскольку исходные и обратные матрицы сохраняют свою “треугольную” форму, в левой части последнего выражения расположена нижняя треугольная матрица, а в правой части - верхняя треугольная. Но равенство в этом случае возможно лишь тогда, когда матрицы являются диагональными. Более того, поскольку содержат единицы на главной диагонали, полученные диагональные матрицы будут единичными, то есть . А отсюда следует, что , но это и означает единственность разложения (2.3).

Рассмотрим матрицу коэффициентов системы линейных алгебраических уравнений следующего вида:

Первый шаг метода Гаусса приводит матрицу к виду

.

Нулевое значение на главной диагонали матрицы вызывает аварийную остановку вычислительного процесса. Нетрудно убедиться, что для исходной матрицы А один из угловых миноров , то есть имеется противоречие условиям теоремы 2.1. Для успешного выполнения процедуры метода Гаусса следует поменять местами строки матрицы А (смена столбцов приведет к необходимости изменить порядок неизвестных), например:

.

Приведение исходной матрицы к новому виду можно интерпретировать как некоторое преобразование вида . Для рассматриваемого случая

.

Теорема 2.2. Если определитель матрицы коэффициентов , то существует матрица перестановок Р такая, что у матрицы все угловые миноры отличны от нуля.

Доказательство теоремы проводится по индукции.

Рассмотрим простейший случай - систему двух уравнений:

.

Если , теорема справедлива при Р = Е , то есть в случае тождественного преобразования.

Пусть теперь . Поскольку , то . Преобразуем исходную матрицу к виду

.

Теперь , то есть при m = 2 теорема справедлива.

Пусть утверждение теоремы также верно и для . Рассмотрим матрицу (обозначения введены ранее):

.

1. Рассмотрим случай . Сформируем матрицу преобразования

и построим новую матрицу

.

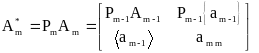В силу сделанного предположения все угловые миноры матрицы отличны от нуля; последний угловой минор также отличен от нуля. В рассмотренном частном случае теорема доказана.

2. Пусть теперь .

Представим разложение определителя матрицы А в виде разложения по последнему столбцу:

.

В силу , существует хотя бы один . Поменяем местами строки матрица А с номерами m и k ( в силу принятого условия ). В результате получаем преобразованную матрицу , у которой угловой минор отличен от нуля. Теперь, в соответствии с доказательством случая 1, уже все угловые миноры матрицы отличны от нуля.

Следствие. Если , то существует матрица перестановок Р такая, что справедливо разложение

PA = LU,

где L - нижняя треугольная матрица с ненулевами коэффициентами на главной диагонали; U - верхняя треугольная матрица с единицами на главной диагонали.