Метод наименьших квадратов
В практических исследования часто
возникает ситуация, когда необходимо
аппроксимировать табличные значения
с помощью приближения (x),
содержащего определяемые коэффициенты
в количестве, меньшем чем число узловых
точек, m < n. По этой причине, в отличие
от рассмотренных ранее способов
аппроксимации функции полиномами
Ньютона, Лагранжа, сплайнами, не
используется условие
- равенство значений функции f(x) и ее
приближения (x) для
заданного числа значений аргумента.
Так, в рассматриваемом методе наименьших
квадратов, “близость” аппроксимирующего
многочлена к самой функции оценивается
с помощью какой-либо нормы, то есть “в
среднем” для всего отрезка, на котором
строится аппроксимация. Для получения
алгоритма построения приближения
воспользуемся полученными соотношениями
(4.26) - (4.31).
Пусть известен набор значений
функции для ряда значений ее аргумента.
Для рассматриваемого случая положим H
=
.
В линейном пространстве размерности
(n+1) скалярное произведение и норма
определяются известным образом:
,
.
Пусть отыскиваемое приближение
зависит от известного числа m параметров
.
Степень отклонения функции f(x) от ее приближения (x) определяется соотношением
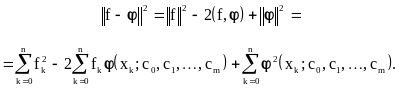(4.32)
Для определения наименьшего отклонения воспользуемся необходимыми условиями минимума функции нескольких переменных:
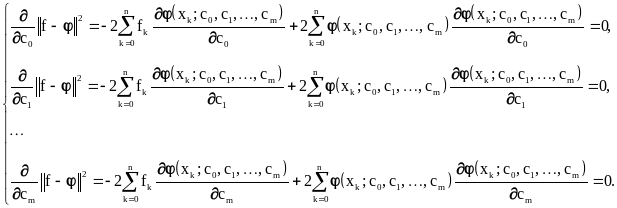
Иными словами, речь идет о решении системы алгебраических уравнений, в общем случае - нелинейных:
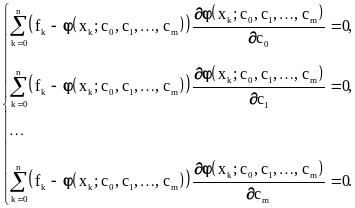
В частном случае, когда приближение (x) представимо в виде
,
оценку (4.32) отклонения функции от ее приближения можно записать в форме:
.
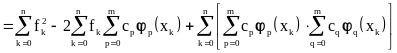Условие минимальности отклонения приближения от функции записывается аналогично представленному выше:
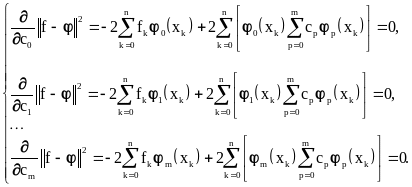
В итоге получена система линейных
алгебраических уравнений относительно
коэффициентов разложения
:
Пример приближения функции | x | на отрезке [-1, 1] с использованием метода наименьших квадратов приведен на рис. 4.7.
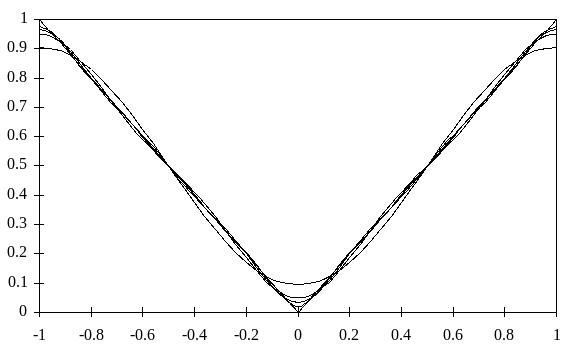
Рис. 4.7. Приближение полиномами Pn функции |x| методом наименьших квадратов
Контрольные вопросы и задания
Сформулируйте задачу аппроксимации. Каковы условия разрешимости этой задачи?
Укажите требования к аппроксимирующим функциям. В каком случае интерполяция называется линейной?
Что представляют собой разделенные разности? Поясните их геометрический смысл.
Укажите порядок построение интерполяционного многочлена Ньютона. Что представляет собой схема Горнера?
Укажите порядок построение интерполяционного многочлена Лагранжа.
Покажите, что полиномы Ньютона и Лагранжа, построенные на одном множестве табличных значений функции, тождественны.
Приведите оценку погрешности аппроксимации функции, заданной таблично, полиномом Ньютона (Лагранжа).
Укажите условия сходимости процесса интерполяции полиномами. Приведите примеры.
Обоснуйте преимущества метода интерполяции для решения нелинейного уравнения.
Опишите способ решение нелинейного уравнения с помощью обратной интерполяции.
Укажите порядок построение интерполяционного многочлена Эрмита.
Опишите идею сплайн-аппроксимации функции и порядок построения кубического сплайна.
Что понимается под сходимостью процесса интерполяции кубическими сплайнами? Сформулируйте и докажите лемму об оценке сходимости по "сеточной" норме.
Сформулируйте и докажите теорему о сходимости процесса интерполяции функции кубическими сплайнами.
Опишите порядок построения наилучшего приближения функции с использованием теории гильбертовых пространств.
В чем заключается метод наименьших квадратов для аппроксимации функции, заданной таблично?