Интерполяция степенными функциями
Пусть в качестве системы функций
рассматриваются полиномы
.
В этом случае D принимает вид определителя Вандермонда1
,
причем
,
если среди множества точек
нет совпадающих. При этом алгебраический
интерполяционный многочлен
всегда существует и определен единственным
образом.
Интерполяционный многочлен Ньютона
Для произвольной функции y(x) определим разделенные разности:
- первая разделенная разность
,
- вторая разделенная разность
,
- третья разделенная разность
,
и так далее.
Рассмотрим геометрический смысл
разделенных разностей. Очевидно, что
и
являются аналогами первых производных
функции y(x) на соответствующих отрезках
и
.
Вторая разделенная разность
аппроксимирует вторую производную
функции y(x) на отрезке
.
Соответственно, третья разделенная
разность - аналог третьей производной
на отрезке
,
и так далее.
Пусть
-
искомый интерполяционный многочлен.
Запишем для него разделенные разности:
,
,
,
...
Отсюда получаем выражение для полинома в виде схемы Горнера1:
Иначе это выражение можно записать в такой форме:
Эта цепочка конечна и содержит (n+1)
слагаемое. В самом деле,
-
полином степени n; разность
при
обращается в нуль, то есть
является корнем выражения
,
и следовательно, оно без остатка делится
на разность
.
Но в этом случае
оказывается полиномом степени (n-1).
Соответственно,
- полином степени (n-2), и так далее. В
итоге,
- полином степени (n-n) = 0, то есть константа,
и наконец,
.
В силу условия (4.1) имеет место
,
откуда получаем
,
либо по схеме Горнера
.
Пример 4.1. Построить аппроксимацию функции sin(x) на отрезке [0, /2].
Таблица 4.1
Таблица для интерполяции функции sin по 4 точкам
-
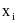
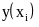
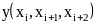
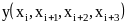
0
0
0,954929659
p/6
0,5
-0,244340364
0,699057028
-0,113871899
p/3
0,866025404
-0,423209925
0,255872631
p/2
1,0
Схема Горнера для аппроксимации заданной функции имеет вид
.
Для значения аргумента
,
отсутствующего в таблице, значение
построенного полинома принимает
значение, равное
.
Вычисление функции sin с погрешностью
не более
дает
.
Таким образом, относительная погрешность
вычисления составляет 0,172 % .
Пример 4.2. Определение корня
нелинейного уравнения
методом обратной интерполяции.
Идея метода обратной интерполяции
заключается в построении полинома
Ньютона для функции x(y) по заданной
зависимости y(x). Особенность данного
случая - необходимость построения
полинома Ньютона на сетке с переменным
шагом по координате
.
Таблица 4.2
Таблица для построения обратной интерполяции функции x(y)
-
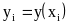
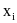
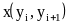
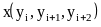
-1,083564434
0,25
0,490578385
-0,573961875
0,5
-0,077430171
0,403097823
0,013912025
0,046234976
0,75
-0,051261555
0,3327975
0,797442541
1,0
Интерполяционный полином Ньютона имеет вид
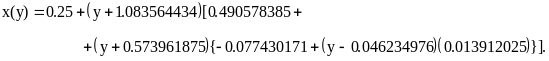
Для y = 0 получаем: x(0) = 0,73301752. Точное решение x = 0,732941247 (невязка уравнения при этом корне равна ). Относительная погрешность вычисления корня равна 0,0104 % .