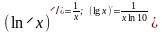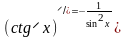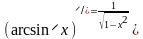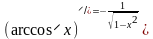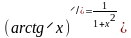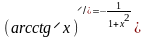- •Курс лекций по дисциплине
- •Введение
- •4. Введение в математический анализ
- •4.1. Понятие функции и аргумента Математический анализ изучает переменные величины и функциональные зависимости между ними.
- •4.2 Пределы функции в точке и на бесконечности
- •4.3. Непрерывность функции и точки разрыва
- •4.4. Производная функции
- •4.5. Дифференцирование функций
- •Практическое занятие 2.
- •I Производная.
- •II. Производная сложной функции
- •3.Найти интервалы вогнутости и выпуклости, а также точки перегиба кривой Гаусса
- •4.Найти асимптоты кривых
- •4.Исследовать функцию с помощью производной и построить ее график
- •4.6. Производные высших порядков
- •4.7. Исследование функций с помощью производных
- •4.7.1. Основные теоремы дифференциального исчисления
- •4.7.2.Признак монотонности функций
- •4.7.3. Локальные экстремумы функций
- •4.7.4. Выпуклость, вогнутость графика функции и точки перегиба
- •4.7.5. Асимптоты графиков функций
- •4.7.6. Общая схема исследования функций и построения графиков
- •Решение:
4.3. Непрерывность функции и точки разрыва
Определение: Функция у=f(х) называется непрерывной в точке х=х0, если выполняются три условия:
Функция определена в точке х0, т.е. существует частное значение функции f(x0);
Существуют равные правый и левый пределы функции в точке х0;
Эти пределы равны частному значению функции в этой точке, т.е.
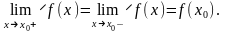
Е сли
в точке х0 не выполняется хотя бы
одно из указанных условий, то точка х0
называется точкой разрыва. Различают
два вида разрывов: разрывы I и II рода.
сли
в точке х0 не выполняется хотя бы
одно из указанных условий, то точка х0
называется точкой разрыва. Различают
два вида разрывов: разрывы I и II рода.
К точкам разрыва I рода относят точки скачка функции, когда
существуют
правый и левый пределы функции, но они
не равны друг другу:
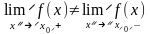 .
Величина h=
.
Величина h= называется величиной скачка.
называется величиной скачка.
К точкам разрыва II рода относят точки
бесконечного разрыва, в которых предел
функции равен бесконечности. Так, функция
точкам разрыва II рода относят точки
бесконечного разрыва, в которых предел
функции равен бесконечности. Так, функция
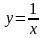 имеет точку бесконечного разрыва II рода
в точке х0=0, т.к.
имеет точку бесконечного разрыва II рода
в точке х0=0, т.к. .
.
Отметим, что все элементарные функции и их комбинации непрерывны в области их определения.
4.4. Производная функции
Переходим к дифференциальному исчислению. Дифференциальное исчисление основывается на понятии производной функции.
Введем
понятие производной функции. Пусть на
некотором множестве D задана непрерывная
функция у = f(х). Возьмем произвольную
точку х из этого множества (хD)
и дадим аргументу приращение
 х.
Причем так, чтобы (х+
х)D
При этом функция получит приращение:
х.
Причем так, чтобы (х+
х)D
При этом функция получит приращение:
 .
.
Определение:
Производной функции у = f(х) называется
предел отношения приращения функции
 к приращению аргумента
к приращению аргумента
 ,
когда приращение аргумента стремится
к нулю
,
когда приращение аргумента стремится
к нулю
 .
.
Производная
обозначается:
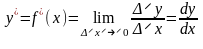 .
.
Е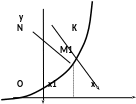 сли
функция у = f(x) имеет конечную производную
в каждой точке множества D, то производная
сли
функция у = f(x) имеет конечную производную
в каждой точке множества D, то производная
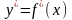 является также функцией от х. Название
производной можно рассматривать как
функцию, произведенную от исходной
функции у = f(x).
является также функцией от х. Название
производной можно рассматривать как
функцию, произведенную от исходной
функции у = f(x).
геометрический и физический смысл производной
Геометрически
производная
определяет угловой коэффициент
касательной к графику функции у=f(x), т.е.
 .
.
Пусть на графике функции у = f(x) задана точка М1(х1,у1). Проведем касательную K и нормаль N к графику функции в заданной точке. Нормаль – это прямая перпендикулярная к касательной.
Угловой
коэффициент касательной равен значению
производной в заданной точке
 ,
а угловой коэффициент нормали из условия
N┼K равен
,
а угловой коэффициент нормали из условия
N┼K равен
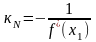 .
.
Тогда можно записать уравнения касательной и нормали к графику функции в заданной точке М1(х1,у1), используя уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом:
 - ур. касательной;
- ур. касательной;
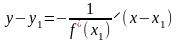 - ур. нормали.
- ур. нормали.
Физический смысл производной заключается в том, что она определяет мгновенную скорость движения.
Пусть материальная точка двигается по закону у = f(t), где у - пройденный путь за время t. Тогда скорость движения в момент времени t = t0 , будет равна:
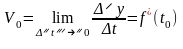 .
.
Ниже будет дан пример расчета скорости и ускорения, исходя из физического смысла первой и второй производных.
4.5. Дифференцирование функций
Определение:
Функция у = f(x) называется дифференцируемой
на множестве D, если в каждой точке этого
множества существует конечная её
производная, т.е. для каждого хD
существует конечный предел
 .
.
Дифференцирование функции – это означает нахождение её производной.
Теорема. Для того, чтобы функция у = f(x) была дифференцируемой на множестве D необходимо и достаточно, чтобы в каждой точке хD этого множества приращение функции ∆у можно было представить в виде: ∆у=А*∆х+α(∆х)*∆х, где А – множитель, который определяется значением производной в точке х: А=f/(x); α(∆х) – б.малая функция при ∆х0.
Действительно, если ∆у=А*∆х+α(∆х)*∆х, то существует конечный предел:
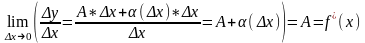 .
.
дифференциал функции
Определение: Дифференциалом функции у=f(x) называется главная линейная часть приращения функции, которая обозначается в виде:
dy= А*∆х=f /(x)* ∆х.
Если возьмём линейную функцию у=х, то дифференциал этой функции будет равен: dх=(x)/* ∆х=1*∆х=∆х или dх =∆х, т.е. дифференциал аргумента равен его приращению.
Тогда дифференциал
любой функции будет равен: dy=f
/(x)*dх.
Откуда производную можно представить
в виде отношения дифференциала функции
к дифференциалу аргумента:
 .
.
Используя обозначение дифференциала, приращение функции можно представить в виде: ∆у=dy+α(∆х)*∆х. Второй нелинейный член приращения: α(∆х)*∆х является б.малой величиной более высокого порядка, чем ∆х и ввиду его малости можно отбросить из выражения. Тогда приращение функции приблизительно равно её дифференциалу: ∆у dy = f/(x)* ∆х.
Если представить приращение функции в виде: ∆у=f(x+∆х)-f(x) f/(x)* ∆х, тогда можно записать f(x+∆х) f(x) + f/(x)* ∆х. Данная формула используется для приближенного расчета значения функции в точке x+∆х по известному значению в точке х.
Теорема о связи между дифференцируемостью и непрерывностью функции. Если функция y=f(x) является дифференцируемой в точке х, то в этой точке она непрерывна.
Отметим, что всякая дифференцируемая на множестве D функция является непрерывной на этом множестве. Однако обратное утверждение не верно – не всякая непрерывная функция является дифференцируемой.
Таблица производных элементарных функций
1. С /= 0, где С = const
2.
где показатель
4.
5.
6.
7.
|
8.
9.
10.
11.
12.
13.
14.
|
Основные правила дифференцирования
Пусть даны две дифференцируемые функции: f(x) и (x).
1. Правило дифференцирования суммы, разности функций:
 ;
;
2. Правило дифференцирования произведения:
 ;
;
3. Правило дифференцирования частного (дроби):
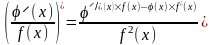 .
.
4. Правило дифференцирования сложной функции.
Пусть
дана функция у = f(u), где u = u(x) - промежуточный
аргумент или промежуточная функция.
Тогда у=f(u(x)) называется сложной функцией.
Производная от сложной функции вычисляется
по формуле:
 .
.
Пример: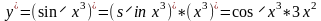 ,
т. к. (sin u)/=(sinu)/*
u/ где u = x3.
,
т. к. (sin u)/=(sinu)/*
u/ где u = x3.

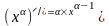 ,
,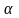 -число
-число
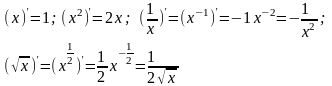 3.
3.
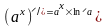
 ,
где е = 2,71...
,
где е = 2,71...