4.7.3. Локальные экстремумы функций

О пределение: Точка х₀ называется точкой локального максимума (или минимума) функции, если в некоторой окрестности точки х₀ функция принимает наибольшее (или наименьшее) значение, т.е. для всех х из некоторой окрестности точки х₀ выполняется условие f(x) f(x₀) (или f(x) 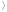f(x₀)).

Точки локального максимума или минимума объединены общим названием - точками локального экстремума функции.

Отметим, что в точках локального экстремума функция достигает своего наибольшего или наименьшего значения лишь в некоторой локальной области. Возможны случаи, когда по значению у_max у_min .

Необходимый признак существования локального экстремума функции

Теорема. Если непрерывная функция у = f(x) имеет в точке х₀ локальный экстремум, то в этой точке первая производная либо равна нулю, либо не существует, т.е. локальный экстремум имеет место в критических точках I рода.

В точках локального экстремума либо касательная параллельна оси 0х , либо имеются две касательные (см. рисунок). Отметим, что критические точки являются необходимым, но недостаточным условием локального экстремума. Локальный экстремум имеет место только в критических точках I рода, но не во всех критических точках имеет место локальный экстремум.

Например: кубическая парабола у = х³, имеет критическую точка х₀=0, в которой производная у^/(0)=0, но критическая точка х₀=0 не является точкой экстремума, а в ней имеет место точка перегиба (см. ниже).

Достаточный признак существования локального экстремума функции

Теорема. Если при переходе аргумента через критическую точку I рода слева направо первая производная у ^/ (x)

1. меняет знак с “+” на “-”, то непрерывная функция у(х) в этой критической точке имеет локальный максимум;

2. меняет знак с “-” на “+”, то непрерывная функция у(х) имеет в этой критической точке локальный минимум

3. не меняет знак, то в этой критической точке нет локального экстремума, здесь имеет место точка перегиба.

Для локального максимума область возрастания функции (у^/ 0) сменяется на область убывания функции (у^/ 0). Для локального минимума область убывания функции (у^/ 0) сменяется на область возрастания функции (у ^/ 0).

Пример: Исследовать функцию у = х³ + 9х² + 15х - 9 на монотонность, экстремум и построить график функции.

Решение:

1. Найдем критические точки I рода, определив производную (у^/) и приравняв ее нулю: у^/ = 3х² + 18х + 15 =3(х² + 6х + 5) = 0

Решим квадратный трехчлен с помощью дискриминанта: х² + 6х + 5 = 0 (а=1, в=6, с=5) D= , , 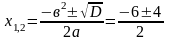х_1к = -5, х_2к = -1.

2) Разобьем числовую ось критическими точками на 3 области и определим в них знаки производной (у^/). По этим знакам найдем участки монотонности (возрастания и убывания) функций, а по изменению знаков определим точки локального экстремума (максимума и минимума).

Результаты исследования представим в виде таблицы, из которой можно сделать следующие выводы:

1. На интер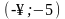вале у ^/(-10) 0 функция монотонно возрастает (знак производной у оценивался по контрольной точке х = -10, взятой в данном интервале);

2. На интервале (-5 ; -1) у ^/(-2) 0 функция монотонно убывает (знак производной у оценивался по контрольной точке х = -2, взятой в данном интервале);

3. На интервале 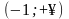у ^/(0) 0 функция монотонно возрастает (знак производной у оценивался по контрольной точке х = 0, взятой в данном интервале);

4. При переходе через критическую точку х_1к= -5 производная меняет знак с "+" на "-" , следовательно эта точка является точкой локального максимума

(y_max(-5) = (-5)³+9(-5)² +15(-5)-9=-125 + 225 - 75 - 9 =16);

5. При переходе через критическую точку х_2к= -1 производная меняет знак с "-" на "+" , следовательно эта точка является точкой локального минимума

( y_min(-1) = -1 + 9 - 15 - 9 = - 16).

х -5 (-5 ; -1) -1

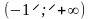
y ^/ + 0 - 0 +

y 16 -16

max min

3) Построение графика выполним по результатам исследования с привлечением дополнительных расчетов значений функции в контрольных точках:

• строим прямоугольную систему координат Оху;

• показываем по координатам точки максимума (-5; 16) и минимума (-1;-16);

• для уточнения графика рассчитываем значение функции в контрольных точках, выбирая их слева и справа от точек максимума и минимума и внутри среднего интервала, например: у(-6)=(-6)³ +9(-6)²+15(-6)-9=9; у(-3)=(-3)³+9(-3)²+15(-3)-9=0;

у(0)= -9  (-6;9); (-3;0) и (0;-9) – расчетные контрольные точки, которые наносим для построения графика;

• п оказываем график в виде кривой выпуклостью вверх в точке максимума и выпуклостью вниз в точке минимума и проходящей через расчетные контрольные точки.