4.7. Исследование функций с помощью производных

4.7.1. Основные теоремы дифференциального исчисления

Основные теоремы дифференциального исчисления лежат в основе исследования функций с помощью производных.

Теорема Ферма. Если дифференцируемая на отрезке [а,b] функция y=f(x) достигает своего наибольшего или наименьшего значения внутри отрезка в некоторой точке х=c, то производная в этой точке равна нулю: f ^/(c) = 0.

Г еометрический смысл теоремы Ферма заключается в том, что если дифференцируемая на отрезке [а,b] функция y=f(x) внутри отрезка в точке х=c имеет наибольшее или наименьшее значение, то касательная к графику функции в этой точке параллельна оси Ох, т.к. угловой коэффициент касательной, который определяется значением производной в этой точке равен нулю: к_к=f ^/(c)=0.

Т еорема Ролля. Если дифференцируемая на отрезке [а,b] функция y=f(x) принимает на концах отрезка равные значения f(a)=f(b), то внутри отрезка [а,b]существует точка х=с, в которой производная равна нулю: f ^/(c) = 0.

Геометрический смысл теоремы Ролля заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), принимающей на концах этого отрезка равные значения f(a)=f(b), существует такая точка х=с внутри отрезка, в которой касательная к графику функции в этой точке параллельна оси Ох.

Т еорема Лагранжа. Если функция y=f(x) дифференцируема на отрезке [а,b], то внутри этого отрезка существует такая точка х=с, в которой производная равна

f ^/(c) = .

Геометрический смысл теоремы Лагранжа заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), существует такая точка х=с внутри отрезка [а,b], в которой касательная к графику функции в этой точке параллельна секущей, соединяющей график на концах отрезка.

Правило Лопиталя. Предел отношения двух б.малых или б.больших функций в точке х=х₀ или на бесконечности при равен пределу отношения их производных:

Правило Лопиталя используется для вычисления пределов при раскрытии неопределенностей типа: .

Примеры. Вычислить пределы:

1. ;

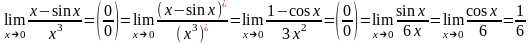2. .

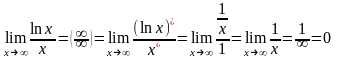4.7.2.Признак монотонности функций

Определение: Функция f(x) называется монотонной на интервале, если она на нем или только возрастает, или только убывает.

Е сли функция монотонно возрастает на интервале, то большему значению аргумента х₂x₁, соответствует большее значение функции: f(x₂)f(x₁).

Если функция монотонно убывает на интервале, то большему значению аргумента х₂x₁, соответствует меньшее значение функции: f(x₂)f(x₁).

На рисунке на интервале функция монотонно возрастает , а на интервале монотонно убывает.

Введем обозначения х = х₂ - х₁ - приращение аргумента и приращение функции: у = f(x₂) - f(x₁). Для возрастающей функции приращения аргумента и функции имеют одинаковые знаки, а следовательно, отношение 0. Для убывающей функции приращения аргумента и функции имеют противоположные знаки, а следовательно, отношение  0. Так как первая производная функции равна , то по знаку производной можно определять участки возрастания и убывания функции.

Необходимый и достаточный признак монотонности функции

Т еорема. Если функция у=f(x) дифференцируема на интервале и ее производная положительна у, то функция на этом интервале монотонно возрастает, а если производная отрицательна у0, то функция на интервале монотонно убывает.

Свяжем это с геометрическим смыслом первой производной, которая определяет угловой коэффициент касательной. Для возрастающей функции угол наклона касательной острый 0⁰90⁰, а следовательно, у^/=tg0. Для убывающей функции этот угол тупой 90⁰180⁰, у^/=tg0.

Отметим, что если в точках первая производная равна нулю или не существует, то в этих точках функция не возрастает и не убывает. Здесь возможны:

• точки перегиба, в которых выпуклость графика функции сменяется вогнутостью или наоборот;

• точки локального экстремума, в которых участок возрастания функции сменяется участком убывания или наоборот.

Определение: Точки, в которых первая производная либо равна нулю, либо не существует, называются критическими точками I рода.