4.7.4. Выпуклость, вогнутость графика функции и точки перегиба

О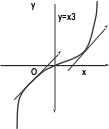 пределение: График дифференцируемой на интервале (a;b) функции называется выпуклым (или вогнутым), если он расположен ниже (выше) любой своей касательной на этом интервале.

Так график кубической параболы у=х³ на интервале выпуклый и лежит ниже своих касательных, а на интервале вогнутый и лежит выше своих касательных.

Отметим, что выпуклость и вогнутость графика функции можно определять по знаку её второй производной. Для кубической параболы у=х³ график на интервале выпуклый, а вторая производная на этом интервале отрицательна у^//=(3x²)^/=6x<0(при x<0). На интервале её график вогнутый, а вторая производная на этом интервале положительна у^//=6x>0(при x>0). Это связано с тем, что вторая производная определяет поведение первой производной. Для выпуклого участка угловой коэффициент касательной, который определяется первой производной, убывает, а следовательно вторая производная отрицательна, а для вогнутого участка наоборот угловой коэффициент касательной возрастает, а следовательно вторая производная положительная.

необходимыЙ и достаточныЙ признак выпуклости и вогнутости

Теорема. Если на интервале (а;b) вторая производная непрерывной функции положительна у^//>0, то график функции вогнутый, а если вторая производная отрицательна у^//<0, то график функции выпуклый.

Определение: Точка, отделяющая выпуклую часть от вогнутой, называется точкой перегиба.

Необходимый признак существования точек перегиба

Теорема. Если непрерывная функция y=f(x) имеет точку перегиба х_п, то в этой точке вторая производная равна нулю (у^//=0) или не существует.

Определение: Точки, в которых вторая производная равна нулю (у^//=0) или не существует называются критическими точками второго рода.

Согласно теоремы точки перегиба бывают только в критических точках второго рода, но не во всех в критических точках второго рода имеют место точки перегиба.

Достаточный признак существования точек перегиба

Теорема. Если при переходе аргументом через критическую точку второго рода х_п вторая производная меняет знак, то эта критическая точка является точкой перегиба.

Так кубическая парабола у=х³ имеет точку перегиба х_п=0, в которой её вторая производная у^//=6х_п=0 и при переходе через эту точку вторая производная меняет знак с «-» на «+».

4.7.5. Асимптоты графиков функций

При исследовании поведения функций на бесконечности при х∞ или вблизи точек бесконечного разрыва второго рода, когда у∞ часто оказывается, что график функции неограниченно близко приближается к некоторой прямой.

Определение: Прямые к которым неограниченно близко приближаются графики функций называются асимптотами.

Асимптоты бывают трех видов: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты имеют место в точках бесконечного разрыва второго рода, когда пределы в этих точках равны бесконечности.

Определение: Прямая х=а называется вертикальной асимптотой графика функции у=f(x), если стремится к бесконечности хотя бы один из пределов: правый 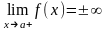или левый .

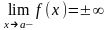В ертикальные асимптоты имеют место, когда функция неопределена в точке при делении на ноль.

Пример. Функция 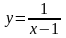неопределена при

х-1=0 или х=1. В этой точке функция терпит бесконечный разрыв второго рода, т.к. -левый предел; 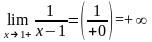-правый предел. Прямая х=1 является вертикальной асимптотой.

Здесь же отметим, что на бесконечности при х∞ эта функция стремится к нулю: у=f(x)  0, т.к. 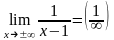=0. Горизонтальная прямая у=0, к которой стремится функция на бесконечности называется горизонтальной асимптотой.

Определение: Прямая у=b называется горизонтальной асимптотой графика функции у=f(x) при х∞, если равен числу b любой из пределов: .

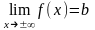Отметим, что эти пределы могут быть разными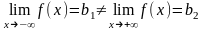 , а следовательно имеют место две горизонтальные асимптоты y=b₁и y=b₂.

Существуют также наклонные асимтоты.

Определение: Прямая у=kx+b называется наклонной асимптотой графика функции y=f(x) при х ∞, если равен нулю любой из пределов .

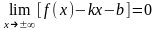Для отыскания наклонной асимптоты используют следующую теорему.

Теорема. Для того, чтобы график функции y=f(x) имел наклонную асимптоту необходимо и достаточно, чтобы одновременно существовали по два конечных предела .

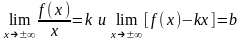С помощью этих пределов определяются параметры (k и b) наклонных асимптот. Причем пределы при х - ∞ и при х + ∞ вычисляются раздельно, т.к. возможны две разные наклонные асимптоты у=k₁x+b₁ и y= k₂x+b₂.

Отметим, что горизонтальная асимптота у=b является частным случаем наклонной асимптоты, когда .
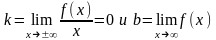