Адамушко Н.Н.

Теория функций

комплексного переменного

Теория функций комплексного переменного

Учебное пособие

по высшей математике

Для специальностей:

220201 – Управление и информатика в технических системах

230105 – Программное обеспечение вычислительной техники и автоматизированных систем

г. Коломна, 2012 г.

УДК 517.5/.8

ББК 22.161.5

А28

Автор: Адамушко Надежда Николаевна

Рецензент: Моос Евгений Николаевич, д.т.н, профессор кафедры ______------------ВМиФ КИ(ф)МГОУ

Адамушко Н.Н.

Теория функций комплексного переменного: курс лекций для студентов инженерных специальностей. – Коломна: КИ (ф) МГОУ, 2012. – 84_с.

Аннотация

В учебном пособии изложены основные понятия теории функций комплексного переменного, применяемой в диаграммной технике анализа систем автоматического регулирования и электрических цепей переменного тока, закладывающей фундамент инженерных знаний студентов.

При изложении последовательно показывается единство математических оснований для функций комплексного переменного и действительных функций действительного переменного.

Все теоретические положения снабжены многочисленными примерами, позволяющими обучаемому глубже понять содержание основного материала и получить начальные навыки оперирования с функциями комплексного переменного. Учебное пособие может быть полезным для самостоятельного изучения курса.

Предназначено для студентов, обучающихся по специальностям: 220201 – Управление и информатика в технических системах;

230105 – Программное обеспечение вычислительной техники и автоматизированных систем.

ISBN © Адамушко Н.Н., 2012

© Коломенский институт

(филиал) ГОУ ВПО

"Московский

государственный открытый

университет", 2012

Содержание

Глава 1.Основные теоремы интегрального исчисления 7

§1 Определение интеграла от функции комплексного переменного и его свойства 7

§2. Теорема Коши. 10

§3 Неопределенный интеграл 12

§4 Интегральная формула Коши и ее приложения. 15

§5 Некоторые теоремы аналитических функций 19

Глава 2 .Функциональные ряды в комплексной области 20

§1. Числовые ряды 20

§2. Функциональные ряды. 23

§3. Степенные ряды. 25

§4. Ряды Тейлора. 29

§5.Ряды по целым отрицательным степеням 34

§6 Ряды Лорана 35

§7 Ряд Лорана в окрестности особой точки. 41

§8 Нули аналитических функций 46

Глава 3. Изолированные особые точки. 52

§1 Изолированные особые точки функции. 52

§2 Определение типа особых точек для суммы, разности, произведения и частного функций. 56

Глава 4. Вычеты и их применение 62

§1 Определение вычета. 62

§2 Вычисление вычетов в полюсе и устранимой особой точке 70

§3 Вычисление контурных интегралов с помощью вычетов 75

Литература 83

ГЛАВА 1

Основные теоремы интегрального исчисления

§ 1. Определение интеграла от функции комплексного

Переменного и его свойства

Определение интеграла

Пусть задана некоторая ориентированная непрерывная кривая и на ней однозначная функция комплексного переменного .

Разобьем кривую произвольно на элементарных дуг точками , записанными в порядке их следования на кривой (точки и - начало и конец кривой соответственно), и на каждой из дуг произвольно возьмем по точке . (см. рис. (1.1). Обозначим .

Интегралом функции вдоль кривой называется предел

, (1.1)

если он существует и не зависит ни от способа разбиения кривой , ни от выбора точек .

Вопрос о существовании комплексного интеграла (1.1) сводится к вопросу о существовании криволинейного действительного интеграла. Действительно, получим, положив ,

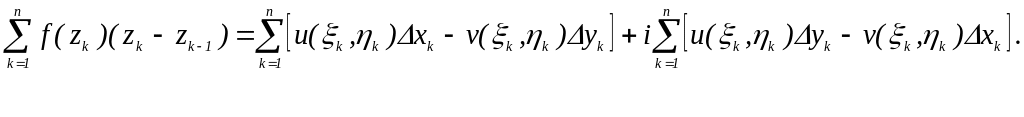Замечаем, что суммы правой части равенства представляют собой интегральные суммы криволинейных интегралов , соответственно. Как следует из теоремы о существовании криволинейного интеграла, для существования интеграла (1.1) достаточно, чтобы кривая была кусочно-гладкой, а функции , кусочно-непрерывными функциями действительных переменных, или что-то же самое, чтобы функция была непрерывной на . Интеграл (1.1) связан с криволинейными интегралами формулой

(1.2)

Пример 1.

Пусть дана постоянная функция . Ее интегральная сумма равна

следовательно, .

В частности, если кривая замкнута , то .

Пример 2.

Пусть .Полагая , получим интегральные суммы , если же положить , то интегральные суммы примут вид . Так как эти суммы имеют один и тот же предел, то их среднее арифметическое имеет тот же предел , равный ,т.к.

Свойства интеграла функции комплексного переменного

1. . (1.3)

2. , (1.4)

где - кривая, составленная из дуг и так, что конец совпадает с началом .

3. , −const. (1.5)

4. . (1.6)

Свойства 1-4 получаются по определению интеграла или из формулы (1.2).

5. (1.7)

где −дифференциал длины кривой , отсчитываемой от начала кривой до произвольной точки ее.

Интеграл записывают также в виде . Действительно, в силу неравенства , модуль интегральной суммы записывается:

, где длины дуги , следовательно, . Переходя к пределу в последнем неравенстве при , получаем формулу (1.7). В частности, если для точки , из формулы (1.7) следует, что .

6. , (1.8)

где гладкая кривая имеет уравнение действительного параметра

Действительно, на основании формулы (1.4) способ вычисления криволинейного интеграла дает

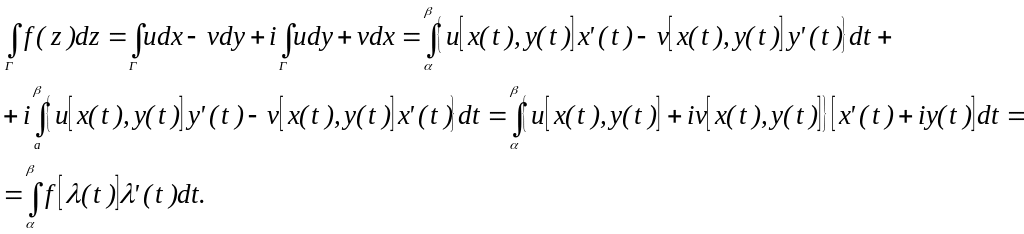Пример 3. Вычислить по окружности, обходимой против часовой стрелки,

интеграл , где уравнение окружности , где .

Применяя формулу (1.4), имеем .

Замечание. Пусть − замкнутая кусочно-гладкая кривая Жордана. Условимся под записью понимать интеграл вдоль контура Г в положительном направлении (т.е. когда область ограниченная кривой Г, остается слева при движении по Г). Когда интегрирование по контуру Г производится в отрицательном направлении, будем писать