
- •Предназначено для студентов, обучающихся по специальностям: 220201 – Управление и информатика в технических системах;
- •230105 – Программное обеспечение вычислительной техники и автоматизированных систем.
- •Содержание
- •Основные теоремы интегрального исчисления
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •§5 Некоторые теоремы аналитических функций
- •Глава 2 функциональные ряды в комплексной области
- •§1. Числовые ряды
- •§2. Функциональные ряды.
- •§3. Степенные ряды.
- •§4. Ряды Тейлора.
- •§5.Ряды по целым отрицательным степеням
- •§6 Ряды Лорана
- •§7 Ряд Лорана в окрестности особой точки.
- •§8 Нули аналитических функций
- •Алгоритм нахождения нулей аналитических функций и определения их порядков.
- •Глава 3 особые точки функций косплексного переменного.
- •§1 Изолированные особые точки функций
- •§2 Определение типа особых точек для суммы, разности, произведения и частного функций
- •Глава 4 вычеты и их применение
- •§ 1. Определение вычета
- •§ 2. Вычисление вычетов в полюсе и устранимой особой точке
- •§3 Вычисление контурных интегралов с помощью вычетов
- •Учебное издание Адамушко Надежда Николаевна Теория функций комплексного переменного
- •140402, Г. Коломна мо, ул. Октябрьской революции, д. 408
§3 Вычисление контурных интегралов с помощью вычетов
Рассмотрим несколько примеров на применение вычетов к вычислению интегралов по замкнутому контуру, используя основную теорему о вычетах(формула 4.4).
Алгоритм
вычисления интегралов
![]() с помощью
вычетов
с помощью
вычетов
1. Найти особые точки функции f(z).
2. Определить, какие из этих точек расположены в области ограниченной контуром C. Для этого достаточно сделать чертёж: изобразить контур C и отметить особые точки.
3. Вычислить вычеты в тех особых точках, которые расположены в области D.
4. Записать результат по формуле ( 4.4):
![]()
![]()
![]() D.
D.
Пример 1.
Вычислить
интеграл
![]() .
.
Записываем решение по алгоритму.
К
 онечными
особыми точками функции
онечными
особыми точками функции
 являются нули знаменателя,
являются нули знаменателя,
 ,
т.е.
,
т.е.
 , k = 0,1,2,3. Заметим, что
все точки – простые нули знаменателя,
следовательно, простые полюсы f(z).
, k = 0,1,2,3. Заметим, что
все точки – простые нули знаменателя,
следовательно, простые полюсы f(z).Контуром интегрирования является окружность
 , а точки
, а точки
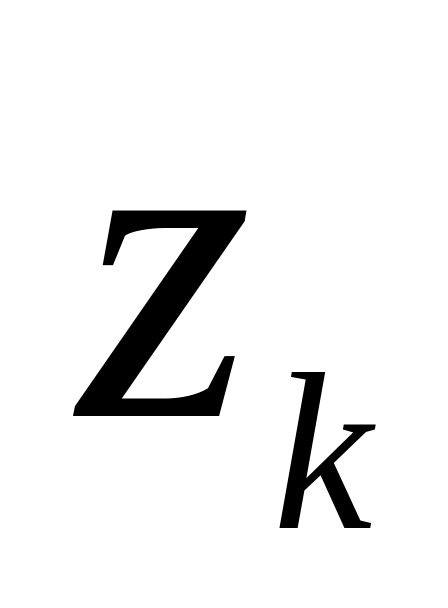 расположены в вершинах квадрата,
вписанного в окружность
(рис.4.5). Поэтому в область, ограниченную
контуром, попадают точки
расположены в вершинах квадрата,
вписанного в окружность
(рис.4.5). Поэтому в область, ограниченную
контуром, попадают точки
 и
и
 . Заметим, что
. Заметим, что
 .
.
3. Находим вычеты в точках по формуле (4.8):
![]() .
.
4. Записываем ответ:

Пример 2.
Вычислить интегралы:
a)
![]() ;
б)
;
б)
![]() .
.
Единственный конечной особой точкой каждой из подынтегральных функций является - существенно особая точка. В обоих случаях она принадлежит области, ограниченной контуром интегрирования. Вычеты находим, раскладывая функции по степеням z (см примеры 2 и 3 §1).
Получаем
![]() .
.
Записываем ответ: а)
![]() ; б)
; б)
![]() .
.
Пример 3.
Вычислить интегралы:
а) ; б)
; б)
![]() .
.
а) Воспользуемся алгоритмом.
1. Находим конечные особые точки функции
![]() -
корни уравнения
-
корни уравнения![]() ,
следовательно,
,
следовательно,
![]() ,
,![]() .
.
2. В область
![]() входят точки
входят точки
![]() ,
так как
,
так как
![]()
и
![]() .
Другие точки не принадлежат кругу
,
так как для них
.
Другие точки не принадлежат кругу
,
так как для них
![]() .
.
3. Точка
- устранимая особая точка функции, так
как, применив
![]() ,
,
 ;
;
поэтому
![]() .
Точка z=-1 является полюсом
первого порядка
,
поскольку она − простой нуль знаменателя,
а числитель при этом не обращается в
нуль, следовательно, функция записывается
в виде
.
Точка z=-1 является полюсом
первого порядка
,
поскольку она − простой нуль знаменателя,
а числитель при этом не обращается в
нуль, следовательно, функция записывается
в виде
![]() .
Вычет вычисляем по формуле (4.8) :
.
Вычет вычисляем по формуле (4.8) :
![]() .
.
4.Запишем ответ:
 .
.
б) Воспользуемся алгоритмом.
1. Особыми точками функции являются нули
знаменателя - корни уравнения
![]() или
или
![]() ,откуда
,откуда
![]() ,
,![]()
2. Из всех найденных корней кругу
![]() принадлежит только одна точка
принадлежит только одна точка
![]() .
.
3,4. Находим вычет в точке - простом полюсе :
 .
.
Записываем ответ:![]() .
.
Пример 4.
Вычислить интегралы:
а)
![]() ; б)
; б)
 .
.
а) Особыми точками функции
![]()
![]() являются простые полюсы
являются простые полюсы
![]() и
и
![]() ,
,
![]() Точка
не принадлежит кругу
,
точки
Точка
не принадлежит кругу
,
точки
![]() расположены на окружности
,следовательно,
принадлежат кругу
.
Применяя формулу ( 4.4), можно найти вычеты
в этих точках, получив ответ:
расположены на окружности
,следовательно,
принадлежат кругу
.
Применяя формулу ( 4.4), можно найти вычеты
в этих точках, получив ответ:
![]() .
.
Чтобы не вычислять вычеты в 15 особых
точках
![]() ,
применим обобщенную теорему о вычетах
(формулу(4.5)). В данном случае она имеет
вид
,
применим обобщенную теорему о вычетах
(формулу(4.5)). В данном случае она имеет
вид
![]() и, следовательно,
и, следовательно,
![]() .
.
Для - простого полюса вычет находим по формуле (4.8):
![]() .
.
Точка
-
устранимая особая точка для
и
![]() .
Вычет вычисляем по формуле (4.10):
.
Вычет вычисляем по формуле (4.10):
![]() .
.
Получаем ответ: ![]() .
.
б) Особыми точками функции
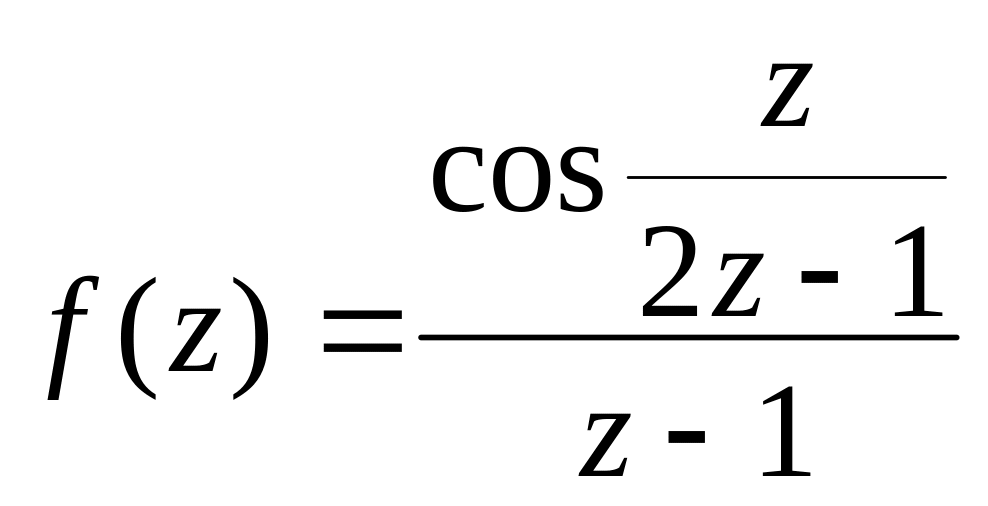 являются точки
- простой полюс и точка
являются точки
- простой полюс и точка
![]() -
существенно особая точка. Обе точки
принадлежат кругу
.
-
существенно особая точка. Обе точки
принадлежат кругу
.
Вычет в точке находим по формуле (4.8):
![]() .
.
Для нахождения вычета в существенно
особой точке
нужно найти коэффициент c-1
в разложении функции
![]() в ряд Лорана по степеням
в ряд Лорана по степеням
![]() .
Для этого записываем разложения в ряд
Лорана функций
.
Для этого записываем разложения в ряд
Лорана функций
![]() и
и
![]() ,
перемножаем ряды и находим c-1
- коэффициент при степени
,
перемножаем ряды и находим c-1
- коэффициент при степени
 .
.
Заметим, вычет в существенно особой
точке
можно вычислить, используя формулу
(4.5).Из равенства
![]() следует
следует
![]() .
.
Поэтому
 и
и

Пример 5.
Вычислить интеграл
![]() ,где
С-граница круга единичного радиуса
с центром в точке
,где
С-граница круга единичного радиуса
с центром в точке
![]() :
:
а)
![]() б)
б)
![]() .
.
Особыми точками подынтегральной функции
являются
![]() - полюс первого порядка,
- полюс первого порядка,
![]() − существенно особая точка и
− существенно особая точка и
![]() - устранимая особая точка(см. пример
4.6).
- устранимая особая точка(см. пример
4.6).
а) В круг
![]() входит точка
входит точка
![]() .
Находим вычет по формуле (4.8):
.
Находим вычет по формуле (4.8):
 .
.
Получаем ответ:
![]() .
.
б) В круг
![]() входят две точки:
входят две точки:
![]() - существенно особая точка,
− устранимая особая точка. Поэтому
- существенно особая точка,
− устранимая особая точка. Поэтому
 ,
,
или, применяя формулу (4.5) (чтобы избежать вычисления вычета в существенно особой точке), получаем
 .
.
Так как
![]() ,
находим
,
находим
![]() по формуле (4.8):
по формуле (4.8):
![]() .
.
Получаем ответ:
![]() .
.
ЛИТЕРАТУРА
1. Лаврентьв М.А. , Шабат Б.В. Методы теории функций комплексного переменного. «Наука», Москва, I 965.
2. Маркушевич А.И. Краткий куре теории аналитических функций. «Наука», Москва, I 966.
3. Свешников А.Г. Тихонов А.В. Теория функций комплексной переменной. «Наука», Москва, I 970.
4. Фукс Б.А.‚ Шабат Б.В. Функции комплексного переменного и некоторые их приложения. Физматгиз. Москва, I 959.
5. Конторович М.И. Операционное исчисление и процессы в электрических цепях. «Наука», Москва, I 964.
Рассмотрено и рекомендовано к рассмотрению
учебно-методического совета КИ (ф)
МГОУ
на заседании кафедры
Высшей и прикладной математики
КИ (ф) МГОУ "22" февраля 2012
г.
протокол № 7
Рекомендовано
к печати решением
учебно-методического
совета
КИ
(ф) МГОУ от
"___" _____________2012
г.
протокол
№ ___
