
- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
1. Прямоугольная система координат на плоскости. Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую единицу масштаба (рис. 3), образуют прямоугольную (или декартову) систему координат на плоскости.
Ось Ох называется осью абсцисс, ось Оу – осью ординат. Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называется координатной плоскостью и обозначается Оху.
Пусть
М
– произвольная точка плоскости. Опустим
из нее перпендикуляры МА
и МВ
соответственно
на оси Ох
и Оу.
Прямоугольными
координатами
х
и у
точки М
будем называть соответственно величины
ОА
и ОВ
направленных отрезков
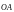 и
и
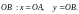

Рис. 3 Рис. 4
Координаты х и у точки М называются, соответственно, ее абсциссой и ординатой.
Тот факт, что точка М имеет координаты х и у, символически обозначают М(х; у). При этом первой в скобках указывают абсциссу, а второй – ординату. Начало координат О имеет координаты (0; 0).
Таким образом, при выбранной системе координат каждой точке М плоскости соответствует пара чисел (х; у) – ее прямоугольные координаты и, обратно, каждой паре чисел (х; у) соответствует, и при этом только одна, точка М на плоскости Оху такая, что ее абсцисса равна х, а ордината у. Значит, прямоугольная система координат на плоскости устанавливает взаимно однозначное соответствие между множеством всех точек плоскости и множеством упорядоченных пар чисел, которое дает возможность при решении геометрических задач применять алгебраические методы.
Оси координат разбивают плоскость на четыре части, их называют четвертями, квадрантами или координатными углами и нумеруют римскими цифрами I, II, III, IV так, как показано на рис. 4. На рис. 4 также указаны знаки координат точек в зависимости от их расположения в той или иной четверти.
Рассмотрим задачу определения расстояния между двумя точками.
Покажем,
что для любых двух точек
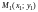 и
и
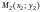 плоскости расстояние
d
между ними
выражается формулой
плоскости расстояние
d
между ними
выражается формулой
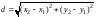 . (2)
. (2)
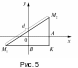 Для
доказательства формулы (2) опустим из
точек
Для
доказательства формулы (2) опустим из
точек
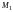 и
и
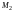 перпендикуляры
перпендикуляры
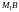 и
и
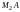 соответственно на оси Оу
и Ох
и обозначим через К
точку пересечения прямых
и
(рис. 5).
соответственно на оси Оу
и Ох
и обозначим через К
точку пересечения прямых
и
(рис. 5).
Точка
К
имеет координаты
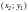 .
Тогда:
.
Тогда:
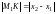 ;
;
 .
Так
как треугольник
.
Так
как треугольник
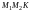 прямоугольный,
то по теореме Пифагора
прямоугольный,
то по теореме Пифагора
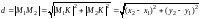 .
□
.
□
2. Полярная система координат. Кроме декартовой системы координат на плоскости широко используется полярная система координат. Эта система состоит из точки О, называемой полюсом, и исходящего из нее луча ОЕ, называемого полярной осью. Задается также единица масштаба для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть М
– любая точка
плоскости. Обозначим через
 расстояние от точки М
до точки О,
а
через
расстояние от точки М
до точки О,
а
через
 − угол, на который нужно повернуть
против часовой стрелки
полярную ось для совмещения с лучом ОМ
(рис. 1).
− угол, на который нужно повернуть
против часовой стрелки
полярную ось для совмещения с лучом ОМ
(рис. 1).
Полярными координатами точки М называются числа и . Число считают первой координатой и называют полярным радиусом, число – второй координатой и называют полярным углом.
Точка
М
с полярными координатами
и
обозначается
 Обычно считают, что полярные координаты
и
изменяются в пределах:
Обычно считают, что полярные координаты
и
изменяются в пределах:

Установим связь между полярными координатами точки и ее прямоугольными координатами, считая, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка М имеет прямоугольные координаты х и у и полярные координаты и (рис. 2). Тогда будем иметь
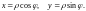 (1)
(1)
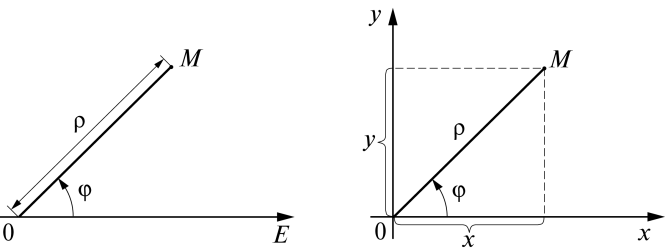
Рис. 1 Рис. 2
Формулы (1) выражают прямоугольные координаты через полярные, а из них полярные координаты через прямоугольные представляются в виде
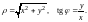 (2)
(2)
Формула
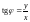 определяет два значения полярного угла
,
т.к.
изменяется в пределах от 0 до
определяет два значения полярного угла
,
т.к.
изменяется в пределах от 0 до
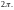
Если
из условий задачи понятно в какой
четверти лежит точка
 то выбираем тот из полярных углов,
который соответствует этой четверти.
В общем случае для определения угла
пользуются соотношениями
то выбираем тот из полярных углов,
который соответствует этой четверти.
В общем случае для определения угла
пользуются соотношениями

Цилиндрическая
система координат.
Кроме
декартовой системы координат в
пространстве часто используется
цилиндрическая
система координат.
Здесь произвольная точка М
в пространстве однозначно определяется
тройкой чисел
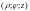 ,
где z
– аппликата точки
М,
,
где z
– аппликата точки
М,
 ,
,
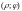 – полярные координаты точки
,
которая
является проекцией точки М
на плоскость Оху
(рис. 3).
– полярные координаты точки
,
которая
является проекцией точки М
на плоскость Оху
(рис. 3).
С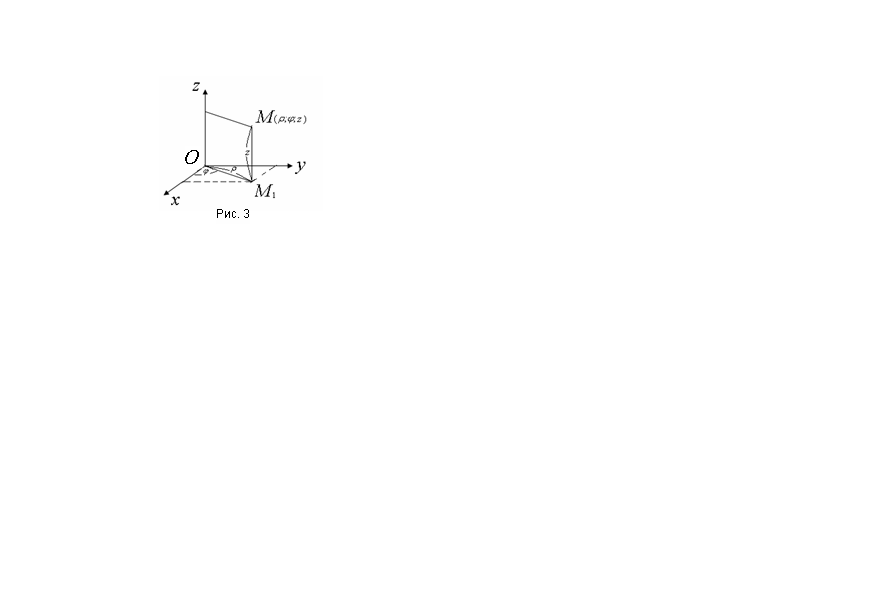 читаем,
что полярная ось на плоскости Оху
совпадает с положительным направлением
оси Ох
при совмещении их начал. Тогда (см.
рис. 3) легко
убедиться, что имеют место формулы:
читаем,
что полярная ось на плоскости Оху
совпадает с положительным направлением
оси Ох
при совмещении их начал. Тогда (см.
рис. 3) легко
убедиться, что имеют место формулы:
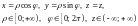 (3)
(3)
Они
выражают декартовы координаты
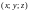 точки М через
ее цилиндрические координаты
точки М через
ее цилиндрические координаты
 .
.
3.Уравнение
линии на плоскости. Уравнение прямой
на плоскости.Важным
понятием аналитической геометрии
является понятие уравнения линии.
Рассмотрим на плоскости прямоугольную
систему координат
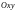 и некоторую линию L
(рис.1), заданную уравнением
и некоторую линию L
(рис.1), заданную уравнением
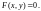 (1)
(1)
Соотношение (1) называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты точек, не лежащих на этой линии.
При
этом на функцию
 должны быть наложены ограничения так,
чтобы, с одной стороны, уравнение это
имело бесконечное множество решений
и, с другой стороны, чтобы это множество
решений не заполняло «куска плоскости».
должны быть наложены ограничения так,
чтобы, с одной стороны, уравнение это
имело бесконечное множество решений
и, с другой стороны, чтобы это множество
решений не заполняло «куска плоскости».
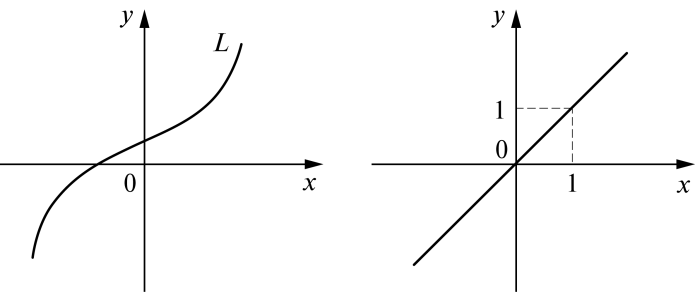
Рис. 1 Рис. 2
Если (1) является уравнением линии L, то говорят, что уравнение (1) определяет или задает линию L.
Линия L может определяться не только уравнением вида (1), но и уравнением вида
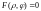 , (2)
, (2)
содержащим полярные координаты.
Примеры определения линий уравнениями:
1)
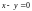 .
Записав это уравнение в виде
.
Записав это уравнение в виде
 ,
заключаем, что множеством точек,
координаты которых удовлетворяют
данному уравнению, являются биссектрисы
I
и III
координатных углов (рис.2);
,
заключаем, что множеством точек,
координаты которых удовлетворяют
данному уравнению, являются биссектрисы
I
и III
координатных углов (рис.2);
2)
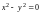 .
Запишем уравнение в виде
.
Запишем уравнение в виде
 .
Заключаем, что множество точек,
координаты которых удовлетворяют этому
уравнению, это две прямые, содержащие
биссектрисы четырех координатных углов
(рис.3);
.
Заключаем, что множество точек,
координаты которых удовлетворяют этому
уравнению, это две прямые, содержащие
биссектрисы четырех координатных углов
(рис.3);
3)
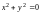 .
Множество точек, координаты которых
удовлетворяют этому уравнению, состоит
из одной точки (0;0). Здесь уравнение
определяет вырожденную линию;
.
Множество точек, координаты которых
удовлетворяют этому уравнению, состоит
из одной точки (0;0). Здесь уравнение
определяет вырожденную линию;
4)
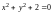 .
Так как при любых
.
Так как при любых
 и
и
 числа
числа
 и
и
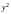 неотрицательны, то
неотрицательны, то
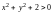 .
Нет ни одной точки, координаты которой
удовлетворяют данному уравнению, т.е.
данное уравнение определяет «пустое»
множество;
.
Нет ни одной точки, координаты которой
удовлетворяют данному уравнению, т.е.
данное уравнение определяет «пустое»
множество;
5)
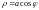 ,
где
,
где
 – постоянная, переменные
и
– полярные координаты. Обозначим через
M
точку с полярными координатами
– постоянная, переменные
и
– полярные координаты. Обозначим через
M
точку с полярными координатами
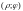 ,
через
,
через
 – точку с полярными координатами
– точку с полярными координатами
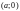 (рис.4). Если
,
где
(рис.4). Если
,
где
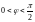 ,
то угол
,
то угол
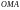 – прямой. Верно и обратное. Следовательно,
множество точек, полярные координаты
которых удовлетворяют данному уравнению
– окружность с диаметром
– прямой. Верно и обратное. Следовательно,
множество точек, полярные координаты
которых удовлетворяют данному уравнению
– окружность с диаметром
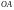 (рис.4);
(рис.4);

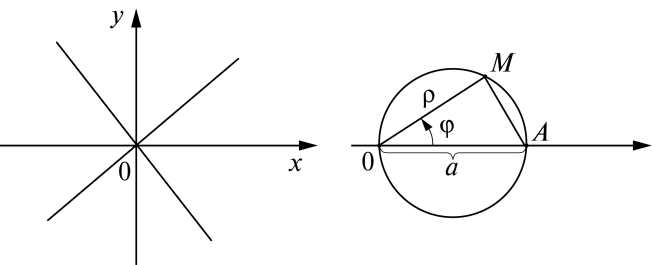
Рис. 3 Рис. 4
6)
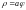 ,
где постоянная
,
и
полярные координаты. Пусть M
– точка с полярными координатами
.
Если
,
где постоянная
,
и
полярные координаты. Пусть M
– точка с полярными координатами
.
Если
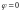 ,
то
,
то
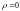 .
Таким образом, при увеличении угла
точка
.
Таким образом, при увеличении угла
точка
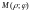 ,
начавшая свое движение в полюсе, движется
вокруг него, одновременно удаляясь от
полюса. Множество точек, полярные
координаты которых удовлетворяют
уравнению
,
называется спиралью
Архимеда
(рис.5).
При этом предполагается, что
может принимать любые неотрицательные
значения.
,
начавшая свое движение в полюсе, движется
вокруг него, одновременно удаляясь от
полюса. Множество точек, полярные
координаты которых удовлетворяют
уравнению
,
называется спиралью
Архимеда
(рис.5).
При этом предполагается, что
может принимать любые неотрицательные
значения.
Если
точка
 совершит один полный оборот вокруг
полюса, то
возрастет
на
совершит один полный оборот вокруг
полюса, то
возрастет
на
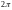 ,
а
– на
,
а
– на
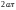 ,
т.е. спираль рассекает любую прямую,
проходящую через полюс, на равные отрезки
длины
(не считая отрезка, содержащего полюс).
,
т.е. спираль рассекает любую прямую,
проходящую через полюс, на равные отрезки
длины
(не считая отрезка, содержащего полюс).
Рассмотрим теперь обратную задачу: для заданного какими-либо его свойствами множества точек, т.е. для заданной линии L, найти ее уравнение.
3 Общее уравнение прямой.
Утверждение 1. В прямоугольной системе координат любая прямая задается уравнением первой степени
 , (7)
, (7)
и,
обратно, уравнение (7) при произвольных
коэффициентах
 (
и
(
и
 одновременно не равны нулю) определяет
прямую в прямоугольной системе координат
.
одновременно не равны нулю) определяет
прямую в прямоугольной системе координат
.
 Доказательство.
Докажем вначале первую часть утверждения.
Если прямая не перпендикулярна оси
Доказательство.
Докажем вначале первую часть утверждения.
Если прямая не перпендикулярна оси
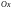 ,
то, как было показано в п.1, она
определяется уравнением первой степени
,
то, как было показано в п.1, она
определяется уравнением первой степени
 ,
т.е. уравнением
вида (5), где
,
т.е. уравнением
вида (5), где
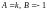 и
и
 .
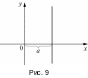
Если прямая перпендикулярна оси
,
то все ее точки имеют одинаковые абсциссы,
равные величине
.
Если прямая перпендикулярна оси
,
то все ее точки имеют одинаковые абсциссы,
равные величине
 отрезка, отсекаемого прямой на оси
(рис.2).
отрезка, отсекаемого прямой на оси
(рис.2).
Уравнение
такой прямой имеет вид
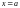 ,
т.е. (7), где
,
т.е. (7), где
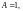
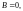
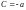 .
Первая часть утверждения доказана.
.
Первая часть утверждения доказана.
Докажем вторую часть утверждения. Пусть дано уравнение (7), где хотя бы один из коэффициентов или не равен нулю.
Если
 ,
то (7) можно записать в
виде
,
то (7) можно записать в
виде
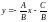 .
Полагая
.
Полагая
 ,
получаем уравнение
,
то
есть
уравнение вида (4), которое определяет
прямую. Если
,
получаем уравнение
,
то
есть
уравнение вида (4), которое определяет
прямую. Если
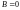 ,
то
,
то
 ,
и (5) примет вид
,
и (5) примет вид
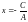 .
Обозначая
.
Обозначая
 ,
получаем
,
т.е. уравнение прямой, перпендикулярной
оси
.
□
,
получаем
,
т.е. уравнение прямой, перпендикулярной
оси
.
□
Линии вида (7) называются линиями первого порядка. Уравнение вида называется общим уравнением прямой, или полным уравнением прямой. При различных значениях оно определяет всевозможные прямые.
4. Неполные уравнения первой степени. Уравнение прямой в «отрезках». Рассмотрим три частных случая, когда уравнение является неполным, т.е. один из коэффициентов равен нулю:
1)
 ;
уравнение имеет вид
;
уравнение имеет вид
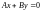 и определяет прямую,
проходящую через начало координат;
и определяет прямую,
проходящую через начало координат;
2)
 ;
уравнение имеет вид
;
уравнение имеет вид
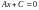 и определяет прямую,
параллельную оси
и определяет прямую,
параллельную оси
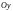 .
В частности, уравнение
.
В частности, уравнение
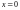 определяет
ось ординат;
определяет
ось ординат;
3)
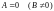 ;
уравнение имеет вид
;
уравнение имеет вид
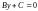 и определяет прямую,
параллельную оси
.
В частности, уравнение
и определяет прямую,
параллельную оси
.
В частности, уравнение
 определяет
ось абсцисс.
определяет
ось абсцисс.
Рассмотрим
теперь уравнение
при условии, что ни один из коэффициентов
не равен нулю, т.е. уравнение (7) является
полным. Преобразуем его к виду .
.
Вводя
обозначения
,
 ,
получаем
,
получаем
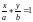 . (8)
. (8)
Уравнение
(8) называется уравнением
прямой «в
отрезках».
Числа
и
 является величинами отрезков, которые
прямая отсекает на осях координат. Эта
форма уравнения удобна для геометрического
построения прямой.
является величинами отрезков, которые
прямая отсекает на осях координат. Эта
форма уравнения удобна для геометрического
построения прямой.
4. Линии второго порядка
Общее уравнение линии второго порядка имеет следующий вид:
 , (1)
, (1)
где
A,
B,
C,
D,
E,
F
– любые заданные числа, но A,
B
и C
одновременно
не равны нулю
 .
.
Теорема 1. Пусть в прямоугольной системе координат Оху задано общее уравнение линии второго порядка (1). Тогда существует такая прямоугольная система координат, в которой уравнение (1) принимает один из следующих девяти простейших (канонических) видов:
эллипс
 ;
;мнимый эллипс
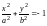 ;
;пара мнимых пересекающихся прямых
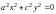 ;
;гипербола
 ;
;пара пересекающихся прямых
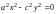 ;
;парабола
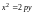 ;
;пара параллельных прямых
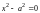 ;
;пара мнимых параллельных прямых
 ;
;пара совпадающих прямых
 .
.
В этих формах х и у равноправны, т.е. их можно менять местами.
