
- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
45. .Первообразная функция и неопределенный интеграл.
Задача интегрального исчисления – восстановление ф. по известным ее производным. F(x) наз. первообразной ф. к функции f(x) на нек. числовом промежутке I если ф. F(x) дифференцируема на I и в каж. точке этого промежутка производная ф. F(x) равна значению ф. f(x). F(x)= f(x) для всех хЄ I.Например ф. F(x)=cosx явл. первообразной к ф. f(x)=-sinx на всей числовой прямой R, т.к. производная cosx это –sinx. Первообразная ф. –sinx будут cosx-3; cosx+5 и т.д. В общем случае cosx+C. Теорема1:2е дифф-мые на числовом промежутке I ф. F(x) и Ф(х) явл. первообразными одной и той же ф. тогда и только тогда, когда они отличаются на постоянной, т.е. Ф(х)=F(X)+C, C=const. Из этой теоремы следует, что для нахождения первообразной ф. f(x) на числовом промежутке I достаточно:1.Найти первообразную F(x) на промежутке I.2.Семейство всех первообразных задается формулой: F(x)+C. Неопределенный интег. от ф. f(x) на числовом промежутке I наз. совокуп. ее всех пнрвообр. на этом числовом промежутке и обозначается ∫f(x)dx. ∫знак интеграла, f(x) – подинтегральная ф., f(x)dx – подинтегральное выражение, х – переменная интегрирования. Если F(x) – какая-либо первообр. к ф. f(x) на числовом промежутке I, то ∫f(x)dx=F(x)+C, для всех х €I. С геометрической точки зрения неопределенный интег. представляет собой семейство плоских прямых(интег. прямых), смещ. относительно друга вдоль оси ординат в прямой декартовой системе координат Оху.
48. Понятие определенного интеграла и его геометр. Смысл.
Рассмотр. Ф-ию у= f(х), заданную на отрезке[а.в], а<в(см. рис. 1).Отрезок [а.в] точками:
а=х0
<x1
<…<xn-1
<xn
=в. Разобьем на n-
элементарных отрезков [a;x1],
[x1;x2],[
xn-1;в],
длины которых обозначаются через ⌂хi
, т.е. ⌂хi
= хi-хi-1.
В каждом из элементарных отрезков [хi-1;
хi]
возмем произведение точки Сi,
значение ф-ии f(Ci)*
⌂хi
( длина
отрезка), получим произведение: f(Ci)*
⌂хi
Составим
сумму таких произведенй: Sn=
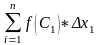 (1)
(1)
Сумма
(1) наз-ся интегральной суммой Римена
ф-ии у= f(х)
на отрезке[а.в]. Обозначим через ג-
длину наиб. Из отрезка[хi-1;
хi],
т. е. ג
=
 .Определ.
интеграл ф-ии у= f(х)
на отрезке[а.в] наз-ся конечный предел
ее интегральной суммы, когда число
отрезка в разбиении не ограничивает
возрастания, а длина наиб. Стремится к
0.
.Определ.
интеграл ф-ии у= f(х)
на отрезке[а.в] наз-ся конечный предел
ее интегральной суммы, когда число
отрезка в разбиении не ограничивает
возрастания, а длина наиб. Стремится к
0.
 При этом числа а и в наз-ся нижн. И верх.
Пределами интегрирования, отрезок
[а.в]- промежуток интегрирования f(х)-
подынтегральная ф-ии. Ф-ия f(х)
для котор. на отрезке[а.в] сущ. Интеграл
наз-ся интегрируемой на этом отрезке.
Необходимым усл. интегрированности
ф-ии у= f(х)
на отрезке[а.в] явл. Ее ограниченность
на этом отрезке. Справедливо утверждение
:1)если Ф-ия f(х)
интегрируема на отрезке[а.в], то она
интегрируема и на любом отр.[c;d]
, содержащемся в [а.в]; 2) если Ф-ия f(х)
непрерывна на отрезке[а.в] или имеет
конечное число точек разрыва на этом
отрезке , то она интегрируема на
отрезке[а.в]. Геометр. Смысл определ.
Интеграла. Определ. Интеграл от
непрерывной на отрезке[а.в] ф-ии у= f(х),
есть S
(площадь ) криволенейной трапеции ( с
учетом знака ф-ии) , огранич. графиком
Ф-ии f(х),
осью ОХ и отрезками прямых х= а ,х=в, т.е.
При этом числа а и в наз-ся нижн. И верх.
Пределами интегрирования, отрезок
[а.в]- промежуток интегрирования f(х)-
подынтегральная ф-ии. Ф-ия f(х)
для котор. на отрезке[а.в] сущ. Интеграл
наз-ся интегрируемой на этом отрезке.
Необходимым усл. интегрированности
ф-ии у= f(х)
на отрезке[а.в] явл. Ее ограниченность
на этом отрезке. Справедливо утверждение
:1)если Ф-ия f(х)
интегрируема на отрезке[а.в], то она
интегрируема и на любом отр.[c;d]
, содержащемся в [а.в]; 2) если Ф-ия f(х)
непрерывна на отрезке[а.в] или имеет
конечное число точек разрыва на этом
отрезке , то она интегрируема на
отрезке[а.в]. Геометр. Смысл определ.
Интеграла. Определ. Интеграл от
непрерывной на отрезке[а.в] ф-ии у= f(х),
есть S
(площадь ) криволенейной трапеции ( с
учетом знака ф-ии) , огранич. графиком
Ф-ии f(х),
осью ОХ и отрезками прямых х= а ,х=в, т.е.

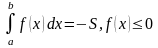
49. Св-во опред. интеграла
1:
2:(линейность опр.инт.)если ф-я y=f(x),y=g(x)
Интегр.на
[a,b],то
для люб. вещ.чисел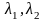 ф-я
ф-я
 интегр.на
[a,b]
интегр.на
[a,b]
То
для люб. Веществ.чис
Также инт. На [a,b] и
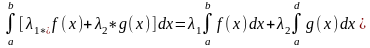
3:(аддитивность опр.инт)если ф-я f(x) инт. На отр.[c,a]и[c,b],то
Она инт. на[a,b],причём опр.инт.)если ф-яик.ф-и

4:(монотон.опр.инт.)если f(x)>=g(x),xэ[a,b],то
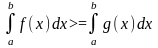
5: (теорема о ср. знач.)для непрер.на отр.[a,b] ф-и f(x) сущ. по
крайн. мере одна точка Eэ[a,b],такая,что
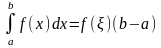
Геометр.теорем о ср.знач обознач,что на[a,b] сущ.по крайн.
мере одна точка, такая,что криволин. трапец,огранич сверхуграфик.
ф-и y=f(x) равновелика прямоуг. С тем же основ.a,b и высотой f( )
