Алгоритм нисходящего разбора

Леворекурсивные грамматики неприменимы для нисходящего разбора.

Используются 2 стека (магазина), счетчик, в котором хранится текущая позиция указателя.

Пусть задана не леворекурсивная грамматика G{N, S, P, Z}. Правила из Р занумерованы для каждого нетерминала А Î N. Упорядочим его альтернативы:

А = a₁ | a₂ | a₃.

A₁ = a₁.

A₂ = a₂.

A₃ = a₃.

Конфигурацию алгоритма будем характеризовать четверкой: (S, i, L₁, L₂), где S – состояние алгоритма.

i – счетчик положения входного указателя.

L₁ – стек, содержащий историю используемых альтернатив и терминальных символов, которые прошли удачное сравнение.

L₂ – вершина слева хранит левовыводимую цепочку, ту ее часть, которая получилась к данному моменту в результате развертки нетерминала.

(q, i, $a, Ab) |¾ (q, i, $a, a_ib). Если существует A_i = a_i (А имеет i альтернатив).

(q, i, $g, aa_ib) |¾ (q, i+1, $gA_ia, a_ib). Если A_i = аa_i и произошло сравнение, то а (терминал входной цепочки) = а (терминал в растущем дереве).

Примечание: i и индекс у a_i – это две разные вещи!

(q, n+1, $p, e) |¾ (t, n+1, $, e);

h(A_i) = i h(p) – номера используемых правил;

h(a) = e.

неудачное сравнение: (q, i, $gA_ia, b) |¾ (q, i, $gA_ia, b) |¾

теперь возврат по дереву |¾ (q, i-1, $g, A_iab).

Пример:

E₁:= T+E.

E₂:= T.

T₁:= F*T.

T₂:= F.

F₁:= (E).

F₂:= a.

(q, 1, $, E₁) |¾ (q, 1, $E₁, T+E) |¾ (q, 1, $E₁T₁,F*T+E) |¾ (q, 1, $E₁T₁F₂,a*T+E) |¾

(q, 2, $E₁T₁F₂a,*T+E) |¾ (b, 2, $E₁T₁F₂a,*T+E) |¾ (b, 1, $E₁T₁,F*T+E) |¾

(q, 1, $E₁T₂,F+E)|¾ (q, 1, $E₁T₂F₂,a+E)|¾ (q, 3, $E₁T₂a+, E) |¾ (q, 3, $E₁T₂a+E₁, T+E) |¾

(q, 3, $E₁T₂a+E₁T₁,F*T+E).

а+а#

E:=E+T|T

|→ |→ |→

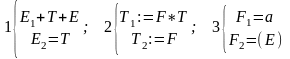
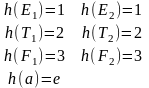
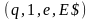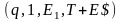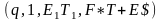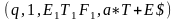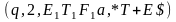|→ |→ - a здесь нужна для возможности вернуться, в случае неудачи мы загружаем в стек терминальный символ |→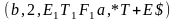 - неудачное сравнение, возврат по дереву

|→ |→ |→ |→

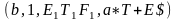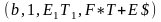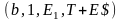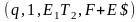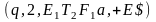|→ |→ |→ - удачное сравнение, перемещаем указатель: ;

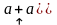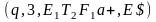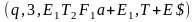|→ |→ |→ далее мы повторим то же самое, но указатель уже передвинется, сравнение будет удачно, но дерево останется, 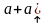, и мы вернёмся назад и возьмём вторую альтернативу |→ 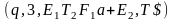|→ |→ 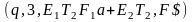- пояснения по поводу последней Т₂ в последних скобках: машина выбрала первую альтернативу и, столкнувшись с неудачей вернулась и выбрала бы

Т₂|→ |→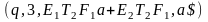

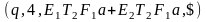
сравниваем удачно

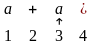
Гомоморфизм .

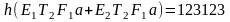Восходящий разбор

Должно быть понятно, что каким бы методом («сверху вниз» или «снизу вверх») мы ни воспользовались для синтаксического разбора стро­ки 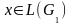, где G — контекстно свободная грамматика, результат дол­жен быть один (это утверждение справедливо при условии допустимости использования обоих методов), так как эти методы отличаются лишь спо­собами построения деревьев.

Если метод синтаксического разбора «сверху вниз» рекомендует построение указанных деревьев на­чиная с корня, то метод «снизу вверх» рекомендует строить их наоборот, начиная с листьев и кончая корнем дерева. Введенные входные строки в последнем случае анализируются слева направо; получаемые в процессе подстроки сравниваются с правыми частями продукции грамматики, а при совпадении заменяются или приводятся к нетерминальному символу, стоящему в левой части таких продукций. В результате такой замены может быть получена сентенциальная форма грамматики, а затем вся процедура повторяется до тех пор, пока полученная сентенциальная форма не примет вид S, где символом S помечен корень дерева вывода. В результате будет получена последовательность схем вывода и соответствующих им приведе­ний, позволяющая построить дерево вывода от листьев до корня. Каждо­му элементу этой последовательности, очевидно, соответствует один ро­дительский узел дерева вывода.

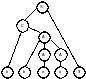
Рассмотрим грамматику G₁, имеющую следующие продукции:

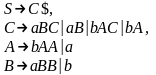
G₁ - одноз­начная грамматика, и, следовательно, любой строке соответст­вует единственное дерево вывода.

Например, дерево вывода для строки 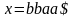приведено на рис. 2, д.

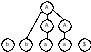
а) б) в)

г) д)

Рис. 2. Дерево вывода для строки

Далее каждому дереву вывода соответ­ствует единственная правосторонняя схема вывода, т. е. такая схема вывода, в которой всегда выводится самый правый нетерминальный символ. Так, дереву вывода, рассмотренному в вышеприведенном примере, соответству­ет правосторонняя схема вывода:

.

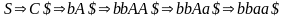Рассматриваемый метод синтаксического разбора «снизу вверх», позволит построить такую схему вывода справа налево. Пример построения дерева вывода для строки bbaa$ показан на рис.1. Подстроку, которая приводится, называют основой правосторонней сен­тенциальной формы, или правосторонней простой фразой. Процесс построе­ния дерева вывода для нашего примера иллюстрируется табл.1.

Таблица1

Правосторонняя сентенциальная форма	Основа	Замещающий символ
bbaa$	а (левый символ)	А
bbАа$	а	А
bbАА$	bАА	А
bА$	bА	С
С$	С$	S

Итак, восходящий разбор связан с отображением входной цепочки в последовательность обращенных правых выводов.

Пусть G(N, S, P, S) – грамматика, правила которой занумерованы 1, 2 … р.

Пусть a - некоторая цепочка в этой грамматике, где a Î (NÈS*).

Тогда правый разбор цепочки a - обращенная последовательность правил, примененных при правом выводе.

1. E:= E+T;

2. E:=T;

3. T:=T*F;

4. T:=F;

5. F:=(E);

6. F:=i.

2 3 5 1 4 6 2

E => T => T*F => T*(E) => T*(E+T) => T*(E+F) => T*(E+i) => T*(T+i) =>

4 6 4 6

=> T*(F+i) => T*(i+i) => F*(i+i) => i*(i+i).

Правый разбор: 6 4 6 4 2 6 4 1 5 3 2.

Набираем в магазине цепочку терминальных символов и смотрим, есть ли в правых частях правил соответствующие нетерминальные символы: МП={Q, S, Г, D, d, q₀, Z, F};

d : Q*S*Г -> Q₁*Г^**D^* - функция отображения, где * - означает цепочки.

Будем рассматривать Z как маркер дна магазина,

S {i, (, ), *, +},

D (1…6) 1,2…6 – номера правил,

Г {N È S}.

Рассмотрим несколько примеров функции отображения:

1. d(q, a, Z) = (q, Za, e),

2. d(q, e, Za) = (q, A, i),

3. d(q, e, ZE) = (r, e, e).

A:= a, q Î Q, r Î F;

Е – начальный символ грамматики,

a – то же самое, что и i (терминал),

b – любой терминальный символ из грамматики.

d (q, e, ZE+T) = (q, E, 1);

d (q, e, ZT) = (q, E, 2);

d (q, e, ZT*F) = (q, T, 3);

d (q, e, ZF) = (q, T, 4);

d (q, e, Z(E)) = (q, F, 5);

d (q, e, Za) = (q, F, 6);

d (q, b, Z) = (q, Zb, e);

d (q, e, ZE) = (q, e, e).

Рассмотрим цепочку a*(a + a):

(q, a*(a + a), Z, e) |¾ (q, *(a + a), Za, e) |¾ (q, *(a + a), ZF, 6) |¾ (q, *(a + a), ZT, 64).

|¾ (q, (a + a), ZT*, 64) |¾ (q, a + a), ZT*(, 64) |¾ (q, + a), ZT*(a, 64).

|¾ (q, + a), ZT*(F, 646) |¾ (q, + a), ZT*(T, 6464) |¾ (q, + a), ZT*(E, 64642).

|¾ (q, a), ZT*(E+, 64642) |¾ (q, ), ZT*(E+a, 64642) |¾ (q, ), ZT*(E+T, 6464264).

|¾ (q, ), ZT*(E, 64642641) |¾ (q, e, ZT*(E), 64642641) |¾ (q, e, ZT*F, 646426415).

|¾ (q, e, ZT, 6464264153) |¾ (q, e, ZE, 64642641532).

Работа преобразователя в данном примере:

на такте 1 преобразователь переносит входной символ в магазин. Всякий раз, когда наверху магазина появится основа, преобразователь может свернуть ее по правилу 2 и выдать при этом номер используемого правила. Это происходит до тех пор, пока верхним символом в магазине не станет начальный символ (Е), за которым следует маркер дна (Z). Это означает, что входная цепочка прочитана, и по правилу 3 попадаем в заключительное состояние.