2. Регулярные выражения и конечные автоматы

Все символы в языках программирования попадают в один из следующих классов:

1. идентификаторы;

2. служебные слова;

3. целые числа;

4. операторы;

5. разделители;

6. комментарии.

Преобразуем диаграмму состояний в конечный автомат:

ДКА={ Q , S , δ , S , Z }

ДКА – детерминированный конечный автомат;

Q – множество состояний (алфавит нетерминальных символов);

S - множество входных символов (алфавит терминальных символов);

δ – функция отображения ( Q×S Q );

S – начальное состояние;

Z– конечное состояние.

Будем говорить, что ДКА допускает цепочку t , если δ (St)=P, где РÎZ.

Можно переписать правила из примера следующим образом:

δ (U0)=Z , δ (V1)=Z , δ (Z1)=U , δ (S1)=U , δ (Z0)=V , δ (S0)=V.

ДКА с состояниями S_i и входной литерой t_j можно представить матрицей B=||b_ij||, элемент которой b_ij=k, где k – номер состояния, и существуют функции отображения δ ( S_i , t_j )=S_k .

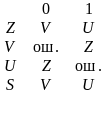
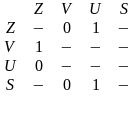
Недетерминированные конечные автоматы

Положение осложняется, если грамматика G содержит правила вида:V: = UT; W: = UT, то есть одинаковые правые части. В диаграмме состояний есть 2 дуги, помеченные символом Т, исходящих из U. Отображение δ становится неоднозначным, и поэтому автомат становится недетерминированным.

Пример:

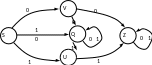
НКА { Q , S , δ , S , Z }, δ(RT) = { W_i }, где W_i Î Q.

Напишем правила через функцию отображения:

δ(S0)=V,Q; δ(S1)=U,Q; δ(Q0)=V,Q; δ(Q1)=U,Q;

δ(U1)=Z; δ(V0)=Z; δ(Z1)=Z; δ(Z0)=Z.

Предположим, у нас есть цепочка 01001. Рассмотрим ее разбор по шагам:

Шаг	Текущее состояние	Остаток входной цепочки	Возможные состояния	Выбранное состояние
1	S	01001	V,Q	Q
2	Q	1001	U,Q	Q
3	Q	001	V,Q	V
4	V	01	Z	Z
5	Z	1	Z	Z

Для любой регулярной грамматики G можно построить диаграмму состояний, а следовательно, НКА. При работе НКА возникает неоднозначность при выборе следующего состояния, если существуют несколько дуг с одинаковой пометкой. Поэтому, прежде чем прийти к выводу о том, что строка не может быть принята НКА, необходимо перепробовать всевозможные последовательности переходов. Следовательно, читать входную цепочку необходимо не один раз, а Õ( n_i ) , где n-число возможных переходов на j шаге.

Пусть мы имеем НКА {Q, S, δ, S, Z}. Нужно построить ДКА{Q’ S, δ’, S’, Z’}.

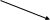
W

0 0

Z

S

1 0 0

1

N

1 0