17.2. Фазовая и частотная модуляция

Пусть модулирующее напряжение изменяется по косинусоидальнему закону . Если это напряжение использовать для изменения начальной фазы радиочастотного колебания по закону

и сделать так, чтобы амплитуда отклонения фазы была пропорциональна амплитуде модулирующего напряжения, то модуляция в этом случае называется фазовой.

Фазомодулированное колебание (ФМ колебание) имеет постоянную амплитуду и переменную начальную фазу

Полная фаза или мгновенное значение фазового угла ФМ колебания определяется уравнением

,

а мгновенная частота

.

Из следует, что при фазовой модуляции имеет место и модуляция частоты, так как мгновенная частота радиочастотного колебания изменяется при этом в такт с модулирующим сигналом.

Тем не менее, следует различать частотную и фазовую модуляции. Частотно-модулированным колебанием (ЧМ колебанием) называется колебание, мгновенная частота которого изменяется по такому же закону, что и модулирующий сигнал. В данном случае модулирующий сигнал изменяется по косинусоиде, поэтому мгновенная частота при частотной модуляции равна

,

где амплитуда отклонения частоты от ₀это_д=f_д, называемая девиацией частоты, пропорциональна амплитуде модулирующего сигнала. Мгновенная фаза ЧМ колебания

.

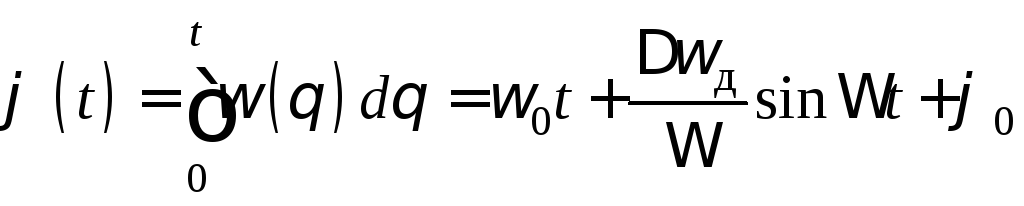В соответствии с ЧМ колебание определяется уравнением

.

Величина отношения девиации частоты к частоте модулирующего сигнала носит название индекса частотной модуляции:

.

Если индекс частотной модуляции <1, частотную модуляцию называют узкополосной.

Если индекс частотной модуляции удовлетворяет неравенству >3…5 для самой высокой частоты модулирующего сигнала, то модуляцию называют широкополосной.

Как при узкополосной, так и при широкополосной модуляции амплитуда отклонения частоты обычно много меньше несущей частоты, т, е .

Индекс частотной модуляции является амплитудой отклонения фазы, измеренной в радианах. Следовательно, =_m.

Частотно-модулированное колебание является в то же время и фазомодулированным. Поэтому оба вида модуляции часто называют угловой модуляцией. Однако при частотной модуляции изменение частоты, а не фазы совпадает с законом изменения модулирующего колебания. Кроме того, при частотной модуляции индекс модуляции обратно пропорционален, модулирующей частоте, тогда как при фазовой модуляции, он от частоты модуляции не зависит.

Когда колебание модулировано гармоническим сигналом, отличить частотную модуляцию от фазовой можно, только сравнив изменения мгновенной фазы модулированного колебания с законом изменения модулирующего напряжения. Очевидно, что спектры высокочастотного колебания при модуляции одним тоном одинаковы при частотной и фазовой модуляции, если одинаковы индексы модуляции. Поэтому при модуляции гармоническим колебанием достаточно рассмотреть спектр какого-либо одного из ЧМ и ФМ колебаний.

17.3. Частотный спектр колебания при угловой модуляции. Общие соотношения

Колебание с угловой модуляцией

,

относительно которого известно, что передаваемое сообщение S(t) заложено в функции(t). Если колебаниеa(t) получено с помощью фазовой модуляции, то(t) иS(t) полностью совпадают по форме и отличаются лишь постоянным коэффициентом. При этом, очевидно, с точностью до постоянного коэффициента совпадают и спектры функций(t) иS(t). В случае же частотной модуляции функция(t) является интегралом от передаваемого сообщенияS(t). Это вытекает из выражений и . Так как интегрирование является линейным преобразованием, то при частотной модуляции спектр функции(t) состоит из тех же компонентов, что и спектр сообщенияS(t), но с измененными амплитудами и фазами.

Отвлекаясь от способа осуществления угловой модуляции – фазовой или частотной – и считая известным и заданным спектр функции (t), можно найти спектр модулированного колебанияs(t). С этой целью выражение преобразуется к виду

.

Из следует, что колебание с угловой модуляцией можно рассматривать как сумму двух "квадратурных" колебаний вида cos₀tиsin₀t, каждое из которых модулировано по амплитуде. Но ранее было установлено, что для определения спектра амплитудно-модулированного колебания достаточно сдвинуть на частоту₀спектр огибающей амплитуд. Следовательно, для нахождения спектра колебанияs(t), определяемого выражением , необходимо сначала найти спектры функцийcos₀tиsin₀t, которые являются огибающими квадратурных колебаний. Перенос этих спектров на частоту₀может быть затем осуществлен таким же образом, как и при обычной амплитудной модуляции.

Из приведенных рассуждений следует, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем при модуляции по амплитуде. Действительно, так какcos₀tиsin₀tявляются нелинейными функциями своего аргумента₀t, то спектры этих функций могут существенно отличаться от спектра функции(t): возможно возникновение кратных и комбинационных частот, как это имеет место при обычных нелинейных преобразованиях спектра.

Это обстоятельство, а также наличие двух "квадратурных" слагаемых показывает, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты ₀, как это имеет место при амплитудной модуляции. Связь между спектрами сообщения и модулированного колебания оказывается при угловой модуляции более сложной.