17.4. Спектр колебания при гармонической угловой модуляции

При гармонической модуляции соотношение принимает вид

.

Учитывая, что множители cos(sint) иsin(sint) являются периодическими функциями времени. Они могут быть представлены разложением в ряды Фурье с коэффициентами, определяемыми бесселевыми функциями:

,

Здесь J_n() – бесселева функция первого родаn-го порядка от аргумента. Графики бесселевых функций нескольких первых порядков приведены на рис. 17.10.

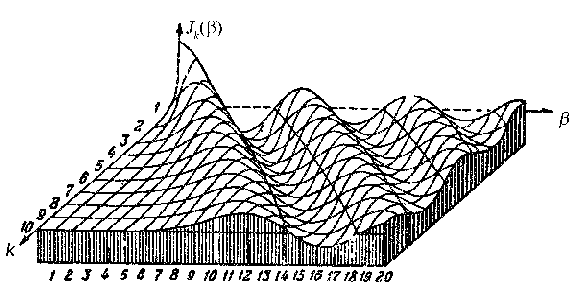
Рис.17.10. Функции Бесселя первого рода

С помощью соотношений и уравнение может быть приведено к виду

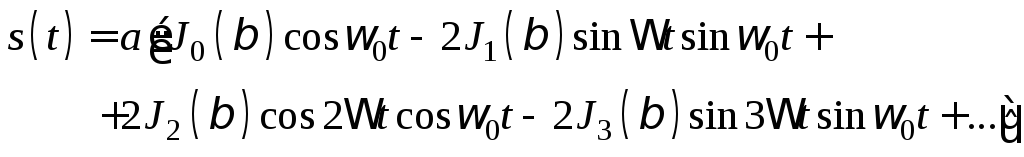
или, иначе,:

Таким образом, при частотной и фазовой модуляции гармоническим колебанием спектр колебания состоит из бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты ₀и отличающихся от нее наn, гдеп –натуральное число. Амплитуда,n-ой боковой составляющей связана с амплитудойамодулируемого колебания и равнаа_п=J_n()a₀, где – индекс модуляции. Отсюда следует, что относительный уровень различных боковых частот определяется величиной индекса модуляции.

Если <<1, так что справедливы приближенные равенства

то выражение переходит в

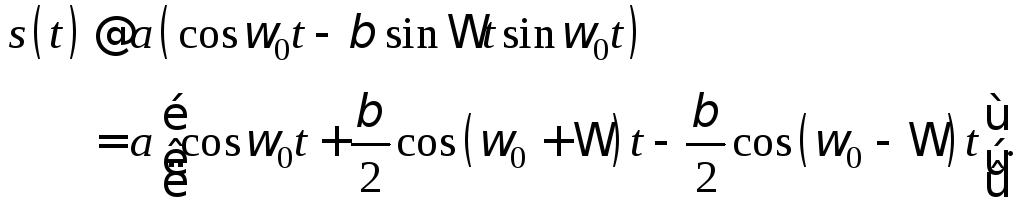
Интересно сравнить это колебание с амплитудно-модулированным колебанием, у которого модулирующая функция (т. е. передаваемое сообщение) такая же, как и при частотной модуляции. Так как выражение получено из , то для удобства сравнения следует представить амплитудно-модулированное колебание в аналогичной форме:

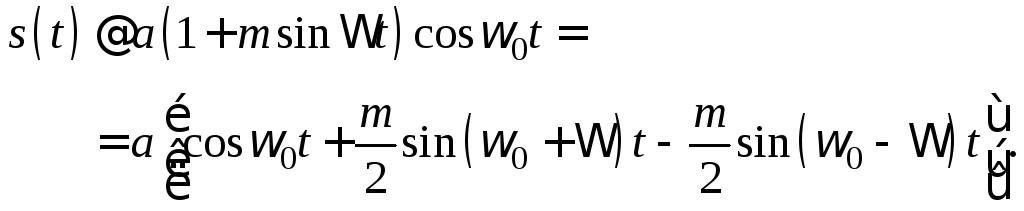
Из сравнения и видно, что при малых значениях  спектр колебания, как и в случае амплитудной модуляции, состоит из составляющей на несущей частоте₀и двух составляющих на боковых частотах: верхней₀+и нижней₀-. Единственное отличие заключается в фазировании боковых составляющих относительно несущего колебания. Это положение иллюстрируется векторной диаграммой, показанной на рис. 17.11,аиб.

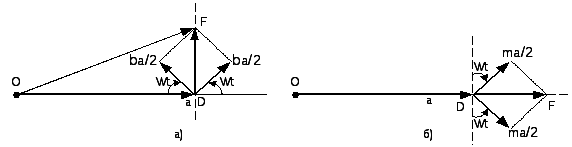
Рис. 17.11. Векторные диаграммы при угловой модуляции с малым индексом а) и амплитудной модуляцииб)

Вектор модуляции DF при угловой модуляции всегда перпендикулярен к направлению вектораOD, изображающего несущее колебание (рис. 1.10,а). ВекторOF, изображающий результирующее колебание, изменяется как по фазе, так и по амплитуде; однако при=_max<<1 амплитудные изменения настолько малы, что ими можно пренебрегать и модуляцию можно в первом приближении рассматривать как чисто фазовую.

Спектральная диаграмма угловой модуляции при <<1 показана на рис. 17.12.

Рис.17.12. Спектры согнала с угловой модуляцией при <<1

Так как фазы отдельных составляющих колебаний этой диаграммой не учитываются, то характер диаграммы получается такой же, как и в случае амплитудной модуляции (рис. 17.3 а). Амплитуды колебаний боковых частот равны, таким образом, в данном случае индекс модуляции совпадает по величине с коэффициентомm, характеризующим глубину изменения амплитуды при амплитудной модуляции. Иначе говоря, ширина спектра при<<1 равна 2как и в случаеAM.

Этот результат показывает, что при очень малых девиациях (_дпо сравнению с) ширина спектра от величины_дне зависит.

При увеличении фазового отклонения, т. е. при возрастании величины , уравнение и диаграмма рис. 17.10 не дают правильного представления о действительной картине явлений при частотной или фазовой модуляции. Это объясняется тем, что с помощью колебания несущей частоты и всего лишь одной пары колебаний боковых частот невозможно представить колебание, частота или фаза которого изменяются в широких пределах по синусоидальному закону, а амплитуда остается строго постоянной.

Для получения правильной картины необходимо учитывать боковые частоты высших порядков, в соответствии с .

При значениях индекса  от 0,5 до 1 приобретает некоторое значение вторая пара боковых частот, ввиду чего ширина спектра должна быть приравнена 4. Далее, при 1<<2 приходится считатьсяс третьей и четвертой парами боковых частот и т. д. Спектрограммы для=1 и=2 приведены на рис. 17.13,аиб.

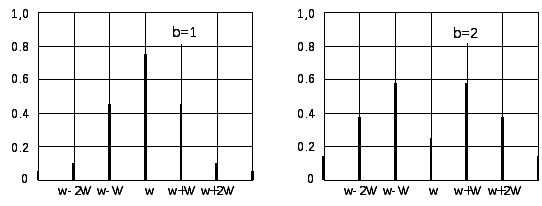
Рис. 17.13. Спектры согнала с угловой модуляцией при =1а) и=2б)

Амплитуды всех составляющих спектра представлены на этих рисунках в виде вертикальных отрезков, длины которых равны J_n(), а расстояния от отрезкаJ₀(), соответствующего амплитуде колебания несущей частоты, равныn, где– частота модуляции, ап – порядковый номер боковой спектральной составляющей. Амплитуда результирующего колебания принята за 1,0 т. е.a=1; обозначенные на рисунках величиныJ_n() дают амплитуды колебаний соответствующих частот в процентах от амплитуды результирующего колебания.

При больших значениях вопрос сводится к выяснению зависимости бесселевой функцииJ_n() от порядкового номераnпри больших значениях аргумента. Оказывается, что приnt>>1 величинаf_n() более или менее равномерна при всех значенияхn, меньших, чем аргумент. Приn, близких к,J_n() образует всплеск, а при дальнейшем увеличениипфункцияJ_n() быстро убывает до нуля. Общий характер этой зависимости показан на рис. 17.14 для=100. Из рисунка видно, что наивысший номерnбоковой частоты, с амплитудой которой необходимо считаться, приблизительно равен индексу модуляции (в данном случаеп=100).

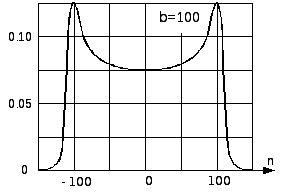
Рис.17.14. Зависимость значения бесселевой функции от номера при аргументе

Приравнивая это максимальное значение n_максвеличине, можно прийти к выводу, что полная ширина спектра модулированного колебания равна

.

Но . Следовательно, при больших индексах модуляции ширина спектра модулированного колебания близка к удвоенной девиации частоты. Универсальная формула связи ширины спектра сигнала с угловой модуляцией с индексом модуляции и девиацией частоты, учитывающая как большие, так и малые индексы модуляции, имеет вид

.

При больших индексах >>1 из следует, что, а при малых, когда<<1,. Если модулирующая функция состоит не из одного колебания, а имеет сложный спектр, вместов следует использовать максимальную частоту_maxв спектре модулирующего сигнала.

В соответствии с определением , выражение "модуляция с малым индексом" эквивалентно выражению "быстрая модуляция", а "модуляция с большим индексом" эквивалентно "медленной модуляции". Можно поэтому сформулировать следующее положение: при быстрой угловой модуляции (когда (_д<) ширина спектра модулированного колебания близка к величине 2; при медленной угловой модуляции (когда_д>) ширина спектра близка к величине 2_д.