Равномерное движение в плоском (щелевом) канале

Движение потока жидкости в плоском канале чаще всего встречается в пластинчатых теплообменниках с плоскими пластинами. Форма поперечного сечения представляет собой прямоугольник, у которого ширина b в несколько раз больше толщины δ (рис. 2.24), т. е. b >> δ.

y

а

x

0 (z)

Рис. 2.24. Расчетная схема к выводу основных закономерностей

течения жидкостей в плоском канале в ламинарном режиме:

а – вид канала по длине; б – поперечное сечение канала

Итак, рассмотрим напорное равномерное движение реальной несжимаемой жидкости в условиях ламинарного режима в направлении оси х (см. рис. 2.24).

Исходной будет система дифференциальных уравнений Навье–Стокса [уравнения (2.43)–(2.45)], которую мы запишем следующим образом:

(2.104)

Так как в соответствии с условием задачи движение жидкости ламинарное, т. е. все частицы движутся только в направлении х, то

и двумя последними уравнениями в системе (2.104) можно пренебречь.

Учитывая, что мы рассматриваем напорное движение жидкости, силой тяжести тоже можно пренебречь, так как величина избыточного давления в канале значительно больше, чем величина гидростатического давления столба жидкости высотой δ, т. е.

a_x = 0.

Кроме того, согласно условию, движение жидкости равномерное, а следовательно, и

Принимая во внимание последние замечания, можно записать

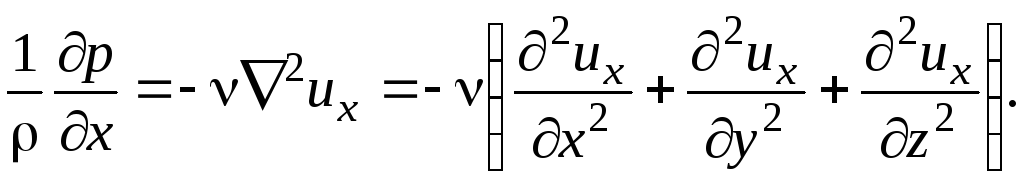(2.105)

Далее запишем уравнение неразрывности потока применительно к нашему случаю:

так как , то данное уравнение приводим к следующему виду:

(2.106)

Как правило, канал пластинчатого аппарата имеет вполне определенные размеры, которые известны или заданы, тогда, переходя к конечной длине и учитывая соотношение (2.106), преобразуем уравнение (2.105):

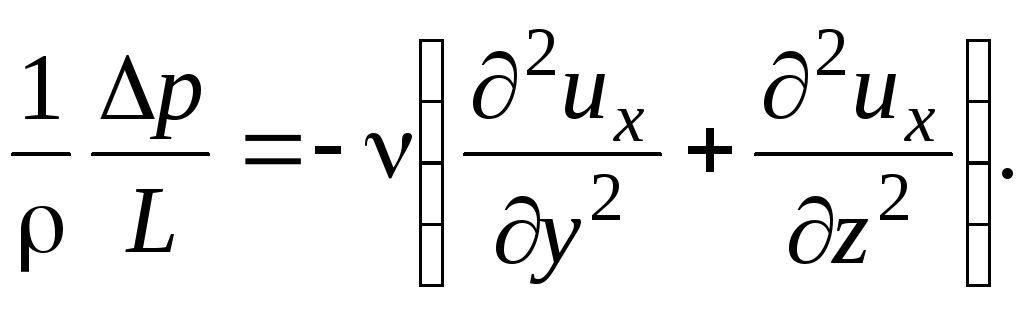(2.107)

Допустим, что канал имеет бесконечную ширину, тогда боковые стенки канала не влияют на изменение локальной скорости частиц жидкости и выполняется условие

при котором влиянием трения жидкости о боковые стенки канала можно пренебречь, откуда

С учетом последнего допущения уравнение (2.107) принимает вид

(2.108)

Знак минус в правой части уравнения (2.108) показывает, что локальная скорость в направлении оси y уменьшается.

Преобразуем уравнение (2.108). Умножим правую и левую его части на и разделим переменные. В результате получим

. (2.109)

Двойное интегрирование уравнения (2.109) позволит нам получить закон распределения локальных скоростей движения частиц в направлении оси y в плоском канале. Решением первого неопределенного интеграла (2.109) будет выражение

(2.110)

где С₁ – постоянная интегрирования.

Значение С₁ можно найти, считая, что на оси канала (y = 0) локальная скорость частиц жидкости равна максимальному значению (), а изменение . Отсюда следует, что С₁ = 0.

Интегрируя второй раз

,

получаем

(2.111)

Значение постоянной интегрирования С₂ найдем из усло- вия при котором . Подставляя данные значения в уравнение (2.111), находим

(2.112)

После подстановки (2.112) в (2.111) получим закон распределения локальных скоростей частиц жидкости при движении жидкости в ламинарном режиме в щелевом канале:

(2.113)

Уравнение (2.113) показывает, что при ламинарном режиме в щелевом канале форма эпюры локальных скоростей также является параболической, как и в трубопроводе круглого поперечного сечения.

Имея закон распределения локальных скоростей по сечению щелевого канала, получим уравнение для теоретического расчета объемного расхода жидкости. Для этого воспользуемся определением объемного расхода, которое вытекает из струйной модели жидкостного потока:

Для того чтобы проинтегрировать данное уравнение, преобразуем его применительно к расчетной схеме, представленной на рис. 2.24. В нашем случае площадь поперечного сечения потока S = bδ. Выделим в данном сечении элементарную площадку dS = bdy, как это показано на рис. 2.24, б. Изменив пределы интегрирования и раскрыв dS, запишем

= (2.114)

Преобразуем правую часть уравнения (2.114):

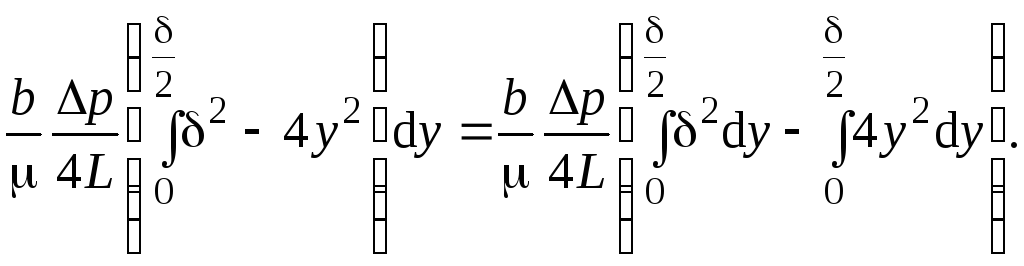(2.115)

Окончательным решением выражения (2.114) будет

. (2.116)

Покажем, как связаны между собой средняя скорость потока и максимальная локальная скорость.

Известно, что

.

Подставим данное выражение в левую часть уравнения (2.116), по- лучим

(2.117)

откуда

(2.118)

Далее получим выражение для расчета . Для этого обратимся к уравнению (2.113), описывающему закон распределения локальных скоростей жидкости в щелевом канале при ламинарном режиме движения:

Максимальная скорость будет находиться на оси живого сечения потока, т. е. при y = 0 , отсюда

. (2.119)

Преобразуем уравнение (2.119) к следующему виду, выразив из него :

(2.120)

Аналогично преобразуем уравнение (2.118), также выразив из него Δр:

(2.121)

Разделим уравнение (2.121) на (2.120), получим

или

откуда

(2.122)

Решим последнюю задачу, т. е. определим потери напора по длине канала. В соответствии с уравнением (2.121)

Выразим толщину канала δ через эквивалентный диаметр d_э, принимая во внимание, что d_э = 2δ. Тогда последнее уравнение примет следующий вид:

. (2.123)

Преобразуем уравнение (2.123), умножив числитель и знаменатель на , и выполним перегруппировку сомножителей:

(2.124)

Разделим левую и правую части уравнения (2.124) на ρg:

(2.125)

и, принимая во внимание преобразования, выполненные ранее при выводе уравнения (2.100), получим

. (2.126)

Первый сомножитель правой части уравнения (2.126) и есть коэффициент трения Дарси λ, т. е.

Как видно из последнего уравнения, численный коэффициент изменился, это связано с изменением формы канала.

Следует отметить, что для каналов других форм, например квадратных и кольцевых, А = 56 и А = 48 соответственно. Кроме того, следует обратить внимание, что при ламинарном режиме движения коэффициент трения λ зависит от критерия Рейнольдса в первой степени.

Сила внутреннего трения, возникающая на твердой поверхности щелевого канала, может быть рассчитана следующим образом.

Нам известно, что сила внутреннего трения Т связана с касательным напряжением τ следующим соотношением (см. уравне- ние (1.9) [1]):

или (для нашего случая)

(2.127)

Напомним, что размерами торцевых стенок щелевого канала мы пренебрегли ввиду их малости, а следовательно, также пренебрегаем их влиянием на распределение локальных скоростей частиц жидкости в направлении оси y.

Касательные напряжения на стенке могут быть определены по уравнению Ньютона для вязкой жидкости:

.

С другой стороны, из уравнения (2.110) при С₁ = 0 следует, что

. (2.128)

Тогда, подставляя уравнение (2.128) в (2.127), получаем

(2.129)