Дифференциальные уравнения движения реальной (вязкой) жидкости Уравнения Навье–Стокса

Полученная система дифференциальных уравнений движения идеальной жидкости (2.40) не учитывает сил внутреннего трения, которые всегда проявляются при движении реальных жидкостей. Как уже отмечалось, одним из важнейших физических свойств жидкости является ее вязкость. Именно вязкость, как физическое свойство жидкости, проявляется только при ее движении и во многом определяет локальную скорость жидкостных частиц как по длине, так и по сечению потока. Поэтому при выводе закона движения реальной (вязкой) жидкости необходимо учитывать силы внутреннего трения.

Рассмотрим установившийся напорный поток несжимаемой вязкой жидкости однородного состава, т. е. ρ = const. Пусть направление движения будет произвольное. Зафиксируем данный поток в декартовой системе координат (рис. 2.13).

Выберем в потоке точку, например точку А. Выделим вокруг этой точки бесконечно малый объем правильной формы, например в виде прямоугольного параллелепипеда, таким образом, чтобы точ-ка А оказалась в центре тяжести этого объема. Допустим, что точка А движется со cкоростью u в направлении движения всего потока и гидростатическое давление в этой точке частицы равно р. Пусть ребра этого параллелепипеда имеют бесконечно малые величины длины dx, dy и dz и параллельны соответствующим осям координат.

По аналогии с выводом уравнений Эйлера введем допущения:

– пусть увеличение u и p происходит плавно в направлении увеличения значений координат x, y и z;

– движение жидкости происходит в изотермических условиях, т. е. в любой точке потока ρ = const и μ = const.

Рис. 2.13. Расчетная схема к выводу уравнений Навье–Стокса

Рассмотрим силы, действующие на выделенный объем жидкости и определяющие скорость его движения. Как и в предыдущем случае, на движущуюся частицу действуют поверхностные и массовые силы. К поверхностным силам относятся силы давления и силы трения окружающей жидкости о выделенный объем. Рассмотрим эти силы более подробно.

Силы давления окружающей жидкости. Количество сил давления будет равно шести, что соответствует количеству граней данного объема. Направлена каждая из этих сил по внутренней нормали к геометрическому центру соответствующей грани (как показано на рис. 2.13). Таким образом, имеем следующие силы: . Величина каждой из этих сил может быть определена из простого соотношения между силой F, давлением р и площадью S, которое известно нам из гидростатики, т. е. F = рS.

Тогда сила, действующая на левую грань abdс,

=

выражение в круглых скобках правой части уравнения есть давление в центре левой грани abdс.

Сила, действующая на правую грань

Аналогично рассуждениям, приведенным ранее, получаем выражения для определения всех остальных сил.

Сила, действующая на заднюю грань ,

Сила, действующая на переднюю грань ,

Сила, действующая на нижнюю грань

Сила, действующая на верхнюю грань ,

Силы трения окружающей жидкости о грани выделенного объема. Силы трения жидкости о грани рассматриваемого жидкостного объема возникают на всех шести гранях. Действуют эти силы в плоскости каждой из граней, создавая при этом касательные напряжения в них. Приложены эти силы по касательной в плоскости рассматриваемой грани к геометрическому центру. Направление действия данных сил противоположно вектору скорости движения этого центра.

Величина каждой из рассматриваемых сил может быть определена из уравнения Ньютона (1.8) [1]. Воспроизведем это уравнение применительно к силам внутреннего трения, действующим в направлении оси x:

Такая запись предполагает, что все частицы совершают плоскопараллельное движение относительно друг друга.

В рассматриваемом случае выделенный объем движется в произвольном направлении, поэтому действие сил внутреннего трения будет проявляться на всех шести гранях. Спроецируем эти силы на ось x.

Проекция силы внутреннего трения для левой грани abdс на ось x

В соответствии с принятыми допущениями сила тормозит эту грань, так как скорость частиц жидкости левее ее меньше.

Проекция силы внутреннего трения, возникающая на правой грани , будет больше, чем на левой. Тогда

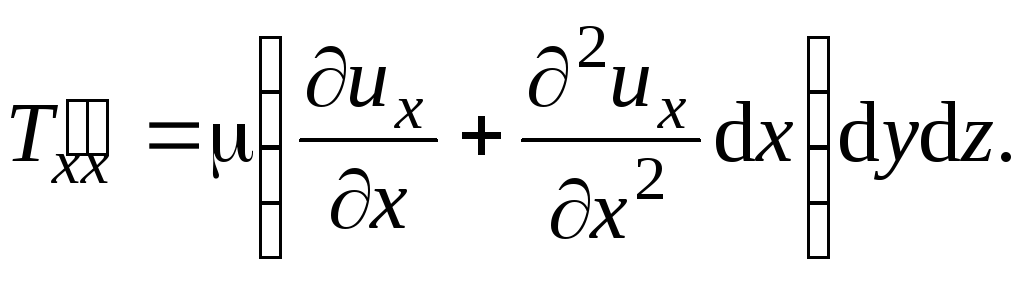
Данная сила положительна, так как жидкость, находящаяся справа, имеет скорость больше и увлекает частицу за собой.

Результирующая этих двух сил

Рассуждая аналогично, определим проекции сил внутреннего трения на ось x для передней и задней граней, допуская увеличение скорости частиц жидкости в направлении увеличения значений y.

Проекция силы внутреннего трения для задней грани bb΄d΄d на ось x

Проекция силы внутреннего трения для передней грани aa΄c΄c на ось x

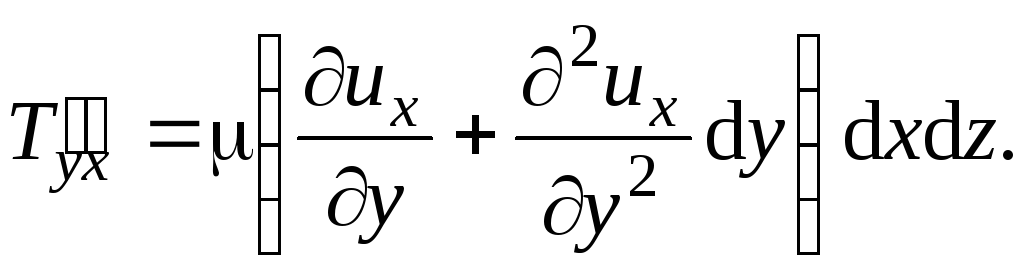
Результирующая этих двух сил

Далее определим проекции сил внутреннего трения на ось x для верхней и нижней граней, допуская увеличение скорости частиц жидкости в направлении увеличения значений z.

Проекция силы внутреннего трения на ось x для нижней гра- ни cdd΄c΄

Проекция силы внутреннего трения на ось x для верхней гра- ни abb΄a΄

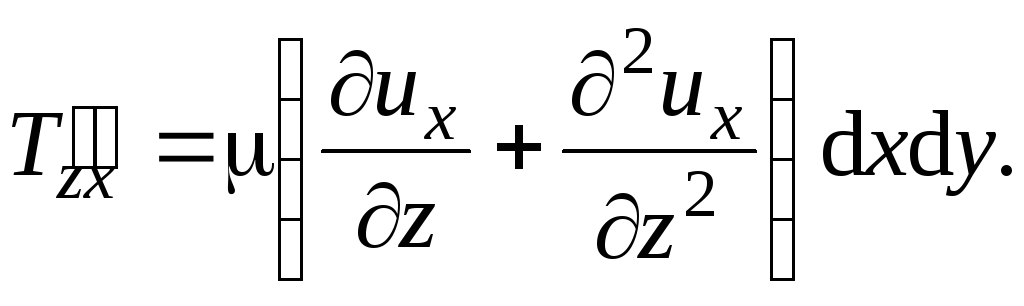
Результирующая этих двух сил

Сумма проекций сил внутреннего трения о все грани параллелепипеда

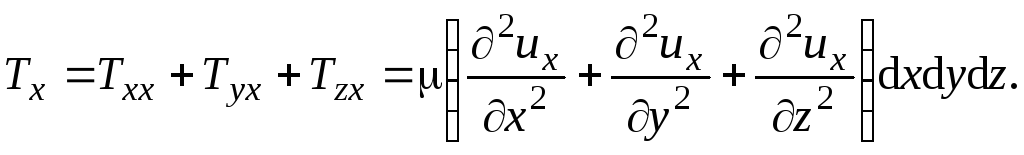
Выражение в круглых скобках правой части данного уравнения есть оператор Лапласа, тогда

К массовым силам относятся силы тяжести G и силы инер- ции G_i.

Массовые силы могут быть записаны как произведение массы на ускорение. В нашем случае масса может быть записана как m = ρdxdydz, где dxdydz – объем параллелепипеда. Ускорение будет определяться природой силового поля. Так как на данном этапе она неизвестна, то обозначим величину ускорения через а. Тогда проекция массовой силы тяжести на ось x

где a_x – ускорение проекции равнодействующей массовых сил на ось x.

Проекция силы инерции на ось x в соответствии с уравне- нием (2.34)

где – ускорение проекции равнодействующей сил инерции на ось х.

Теперь, когда значения всех сил, действующих в направлении оси х, определены, составим баланс сил:

. (2.41)

Подставим соответствующие значения проекций сил в уравнение (2.41):

+ –

+ = 0.

Упростим полученное выражение, раскрыв скобки в первых двух слагаемых и сократив на dxdydz.

В результате получим

. (2.42)

Выполним перегруппировку слагаемых в уравнении (2.42), предварительно сократив все члены уравнения на ρ. Тогда с учетом того, что μ/ρ = ν, получим

(2.43)

Рассуждая аналогично, получим два других уравнения, рассматривающие баланс сил, действующих в направлении осей y и z:

(2.44)

и

(2.45)

где ν – кинематический коэффициент вязкости, м²/с.

Система уравнений (2.43)–(2.45) получила название «уравнения Навье–Стокса³», они представляют собой дифференциальные уравнения движения реальной (вязкой) жидкости.

В общем случае система уравнений Навье–Стокса не замкнута, так как она содержит шесть неизвестных: u_x, u_y, u_z, р, ρ и ν.

В качестве четвертого уравнения, связывающего первые три неизвестных, является уравнение неразрывности потока

В качестве двух последних уравнений, замыкающих систему, используют уравнение состояния среды и уравнение зависимости вязкости от параметров состояния – давления и температуры.

Здесь следует напомнить, что в гидравлике мы рассматриваем потоки несжимаемой жидкости в изотермических условиях, для которых ρ = const и ν = const. В этом случае для замыкания уравнений Навье–Стокса достаточно будет добавить лишь уравнение неразрывности потока.

Уравнения Навье–Стокса позволяют выполнять математические исследования характеристик движения и покоя как реальных, так и идеальных жидкостей.

При необходимости описания движения идеальной жидкости (отсутствуют силы внутреннего трения) из уравнений Навье–Стокса достаточно исключить второе слагаемое правой части уравнения, содержащее вязкость. В результате получим выведенные ранее дифференциальные уравнения движения идеальной жидкости:

Если надо получить характеристики покоящейся жидкости, необходимо уже из уравнений Эйлера убрать слагаемые, содержащие скорость, т. е.

Решение уравнений Навье–Стокса в общем виде представляет собой сложную математическую задачу, связанную с получением решений системы нелинейных дифференциальных уравнений в частных производных второго порядка. Математическая теория таких систем разработана недостаточно строго, однако для частных случаев, описывающих вполне определенные виды течений, точные решения существуют. Рассмотрим один из классических примеров применения уравнений Навье–Стокса для случая течения идеальной жидкости.