Равномерное движение в щелевом канале с одной движущейся поверхностью

Напорное движение жидкости в канале, который образован неподвижной поверхностью и подвижной, имеет место при движении жидкости в зазоре, образованном стенками поршня и цилиндра (рис. 2.25). В этом случае неподвижной твердой поверхностью является поверхность цилиндра, а подвижной – боковая поверхность поршня, совершающая возвратно-поступательное движение вдоль оси цилиндра. Принципиальным отличием данного случая течения от предыдущего является отсутствие равенства нулю локальной скорости частиц, находящихся на твердой стенке поршня.

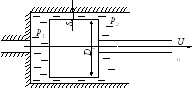
Рис. 2.25. Цилиндропоршневая группа

Выполним расчетную схему (рис. 2.26) и рассмотрим движение поршня в цилиндре. Пусть поршень движется со скоростью U_п. Величину зазора между поршнем и цилиндром обозначим δ, а диаметр поршня – D_п. Давление в левой полости цилиндра p₁, а в правой полости – p₂. Разность этих давлений является движущей силой, побуждающей жидкость к напорному течению через зазор.

T₂

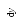
р₁

р₂

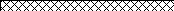
U_п

l

U_п

T₁

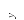
Рис. 2.26. Расчетная схема щелевого канала, образованного

неподвижной и подвижной стенками

Если зазор очень мал, т. е. выполняется условие , так как величина зазора выражается в долях миллиметра, что обычно имеет место при сопряжении подвижных и неподвижных деталей, то щелевой канал можно считать плоским. В этих условиях (см. рис. 2.26) одна плоскость шириной b неподвижна, другая такой же ширины и длиной l перемещается со скоростью U_п.

Выделим в зазоре слой бесконечно малой толщины dy на расстоянии y от неподвижной поверхности и составим уравнение равновесия сил в направлении движения жидкости. Введем некоторые допущения. Силой тяжести и силой инерции можно пренебречь ввиду их пренебрежимо малых величин. Кроме того, исключим влияние силы трения, возникающей на стенках площадью δl, что имеет место для щелей неограниченной ширины b.

Сила трения на нижней поверхности слоя

.

Сила трения на верхней стороне этого же слоя

Равнодействующая данных сил

.

Сила давления на торцевые поверхности слоя (см. рис. 2.26)

В условиях равновесия, при проецировании всех сил на направление движения жидкости, получаем

Выражая из последнего уравнения, получим

(2.130)

Отношение . С учетом последнего соотношения преобразуем уравнение (2.130), умножив числитель и знаменатель на объемный вес . Тогда, принимая во внимание, что , полу-чаем

(2.131)

Неопределенный интеграл выражения (2.131) дает зависимость следующего вида:

. (2.132)

Учитывая, что при ламинарном режиме движения жидкости касательное напряжение τ связано с градиентом скорости зависимостью , преобразуем уравнение (2.132) к следующему виду:

. (2.133)

Интегрируя вторично, получим

. (2.134)

Определим постоянные интегрирования С₁ и С₂ в уравне- нии (2.134). Для этого необходимо задаться граничными условиями. Например, при . Подставляя данное граничное условие в уравнение (2.133), получаем, что .

При , тогда

. (2.135)

Подставим найденные значения постоянных интегрирования в уравнение (2.134), получим закон распределения локальных скоростей по толщине зазора:

. (2.136)

Влияние сил давления и трения на скорость движения частиц учитывается первым слагаемым правой части уравнения (2.136). Влияние скорости перемещения поверхности поршня, вызывающее фрикционное движение частиц жидкости в зазоре, учитывается вторым слагаемым правой части этого уравнения.

В промышленных условиях рассматриваемые силы не всегда действуют одновременно. В этой связи возможны следующие случаи возникновения движения в плоских щелевых зазорах:

– одна стенка подвижна, другая нет, при этом гидравлический уклон отсутствует, т. е. i = 0;

– одна стенка подвижна, другая нет, при этом наблюдается положительный гидравлический уклон, т. е. i > 0;

– одна стенка подвижна, другая нет, при этом наблюдается отрицательный гидравлический уклон, т. е. i < 0.

Рассмотрим вышеперечисленные случаи более подробно в целях получения расчетных зависимостей для ряда параметров, характеризующих эти течения.

Равномерное движение в щелевом канале с одной

движущейся стенкой и одной неподвижной стенкой

при отсутствии гидравлического уклона

В указанном случае наблюдается так называемое течение Куэтта. Движущей силой является сила внутреннего трения, передающая кинетическую энергию от движущейся твердой поверхности к частицам жидкости. Выполним расчетную схему, изображающую такой поток (рис. 2.27). Получим закон распределения локальных скоростей жидкости для этого случая.

Рис. 2.27. Расчетная схема равномерного движения жидкости в щелевом

канале с одной движущейся стенкой и одной неподвижной

стенкой при отсутствии гидравлического уклона

Рассматриваемая ситуация представляет собой частный случай движения, который описывается уравнением (2.136), поэтому в наших рассуждениях примем эту зависимость за исходную. Для рассматриваемого случая i = 0, т. е. первое слагаемое правой части уравнения (2.136)

.

Тогда в соответствии с уравнением (2.136) можно записать, что

. (2.137)

Из уравнения (2.137) следует, что изменение локальной скорости по толщине зазора подчиняется линейному закону, величина локальной скорости зависит от скорости движения твердой поверхности U_п и местоположения рассматриваемой частицы жидкости в щели, т. е. координаты у.

Получим уравнение для расчета объемного расхода жидкости для этого случая. Запишем уравнение неразрывности потока применительно к рассматриваемой расчетной схеме:

, (2.138)

где b – ширина щелевого зазора.

Решением интеграла (2.138) будет зависимость

, (2.139)

из которой видно, что объемный расход жидкости через щелевой канал линейно зависит от толщины зазора.

Средняя скорость потока жидкости может быть рассчитана по уравнению расхода (2.16):

. (2.140)

Сила трения, возникающая на неподвижной поверхности щели, может быть определена из уравнения Ньютона для вязкой жидкости (см. уравнение (1.9) [1]):

,

где – касательные напряжения, возникающие в зазоре между подвижной и неподвижной поверхностями; L – длина щелевого канала.

Градиент скорости определим, дифференцируя уравнение изменения скорости в направлении оси y:

. (2.141)

Из уравнения (2.141) следует, что касательные напряжения в данном случае не изменяются по сечению щелевого зазора и остаются постоянными:

. (2.142)

Эпюра касательных напряжений показана на рис. 2.27.

С учетом уравнения (2.142) сила внутреннего трения может быть определена по зависимости

. (2.143)

Равномерное движение в щелевом канале с одной

движущейся стенкой и одной неподвижной стенкой

в случае положительного гидравлического уклона

В данном случае будет наблюдаться напорное движение жидкости в щелевом канале, при котором и i > 0, т. е. движение жидкости в канале будет определяться не только силой внутреннего трения, но и разностью потенциальных энергий на входе жидкости в канал и на выходе из него. На практике данный случай имеет место в зазоре между поверхностями цилиндра и поршня.

Выполним расчетную схему, которая показана на рис. 2.28.

y

р₁ > р₂

τ

u = 0

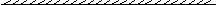
р₁

u_max

р₂

U_п

U_п

Рис. 2.28. Расчетная схема равномерного движения жидкости в щелевом

канале с одной движущейся стенкой и одной неподвижной

стенкой при положительном гидравлическом уклоне

Закон распределения локальной скорости был получен нами ранее [см. уравнение (2.136)], поэтому воспроизведем его для дальнейшего анализа:

;

при этом, если y = 0, то u = U_п, а если y = δ, то u = 0.

Определим градиент скорости:

. (2.144)

Отсюда следует, что при условии вектор максимальной скорости будет находиться на расстоянии (см. рис. 2.28).

Расход жидкости через зазор определим из условия неразрывности потока:

(2.145)

По аналогии с предыдущим анализом определим силу трения на неподвижной поверхности:

.

Равномерное движение в щелевом канале с одной

движущейся стенкой и одной неподвижной стенкой

в случае отрицательного гидравлического уклона

Данный случай будет наблюдаться, когда давление в канале падает в направлении движения поршня, т. е. имеем ситуацию, когда . На практике такой случай встречается при работе насоса двойного действия, шестеренчатого насоса и др. Расчетная схема будет иметь следующий вид (рис. 2.29).

Рис. 2.29. Расчетная схема равномерного движения жидкости в щелевом

канале с одной движущейся стенкой и одной неподвижной

стенкой при отрицательном гидравлическом уклоне

В этом случае закон изменения локальной скорости примет вид

. (2.146)

Определимся с граничными условиями: если y = 0, то u = U_п; если y = δ, то u = 0. Очевидно, что при

Градиент скорости для этого случая

. (2.147)

Максимальное значение скорости будут иметь частицы, находящиеся на расстоянии y, которое можно получить из выраже- ния (2.147), исходя из условия , т. е.

. (2.148)