3.5. Действительные числа

В математике существуют различные построения теории действительного числа:

- по Дедекинду (построение действительного числа с помощью сечений на множестве рациональных чисел),

- по Вейерштрассу (представление действительного числа как бесконечного десятичного ряда),

- по Кантору (построение действительного числа с помощью фундаментальных последовательностей рациональных чисел)…

Но эти построения весьма сложны (не случайно в математике они оформились во второй половине 19 века).

Понятие «действительное число» (как и понятие «бесконечная десятичная дробь»), основные положения теории действительного числа вполне доступны учащимся 7 класса. В настоящее время существует тенденция более раннего изучения действительных чисел, что ускоряет создание цельной системы знаний учащихся о числе, облегчает потребности практики вычислений, позволяет строже изложить некоторые вопросы фундаментальной теории…

Понятие «иррациональное число» появляется в учебниках 8 класса.

Мотивация введения действительных чисел опирается на внутренние потребности математики, а не на практику. Учащиеся убеждаются в необходимости введения новых чисел при решении следующих задач:

- Решить уравнение: х² = 2.

- Найти отношение длины дуги окружности к ее диаметру.

- Найти сторону квадрата, если его площадь 3 см².

- Решить графически уравнение: х² = 3.

- К множеству каких чисел относятся числа 2, 56565…; 7,23233233…; 0, 123123412345…?

Определение иррационального числа дается через отрицание.

Пример: Алгебра – 8(С.А. Теляковский)

1. Доказывается, что «среди рациональных чисел нет такого числа, квадрат которого равен 2».

2. Вводится понятие «действительное число»: «Если к положительным бесконечным десятичным дробям присоединить противоположные им числа и нуль, то получим множество чисел, которые называют действительными числами».

3. Дается определение иррациональных чисел: «Каждую бесконечную десятичную периодическую дробь можно записать в виде отношения m /n, где m – целое число, n – натуральное число. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает отрицание). Иррациональные числа нельзя представить в виде отношения m /n. Таким образом, множество действительных чисел состоит из рациональных и иррациональных чисел.».

4. Приводятся примеры иррациональных чисел.

5. Вводятся «действия» над числами. В школьном курсе действия с иррациональными числами сводятся к операциям с их рациональным приближениями по недостатку и по избытку⁵.

Остановимся более подробно на методике изучения иррациональных чисел.

Рациональные и иррациональные числа

В 5 – 6 классах учащиеся познакомились с обыкновенными дробями. Перед изучением иррациональных чисел целесообразно обобщить эти знания и на новом уровне рассмотреть множество рациональных чисел Q.

В множестве натуральных чисел N операция деления имеет ограниченный характер: если а и в натуральные числа, то не всегда найдется натуральное число х такое, чтобы

ах = в (приведите примеры). Другими словами, в том случае, когда в не делится нацело на а, уравнение ах = в неразрешимо. Чтобы устранить это несовершенство, вводятся дроби, записываемые в виде отношения m/n, где m,n – натуральные числа. При этом число m называют числителем, а число n знаменателем дроби m/n. Вспомним правила действий с дробями:

(1)

Правило позволяет «сокращать» дробь на общий для числителя множитель. Например,. Как видим, равные дроби могут очень различаться по внешнему виду. (Убедитесь, что дробии- равные дроби.) Натуральное числоn можно считать частным случаем дроби, отождествляя его с .

Построенное расширение натурального ряда обозначим через Q⁺ - этоположительные рациональные числа (от латинского ratio - отношение). Умножение в Q⁺ ассоциативно и коммутативно, уравнения вида ах = в, где а и в – любые числа из Q⁺, разрешимы (решением будет х = ). Следовательно, (Q⁺,^.) –коммутативная группа, это – мультипликативная группа положительных рациональных чисел (от латинского multiplication – умножение). Деление в ней осуществляется неограниченно.

Если ноль и отрицательные числа сначала появились как математические абстракции и лишь впоследствии нашли им содержательное толкование, то дроби были известны с древнейших времен:

- Распределение некоторого общего достояния на индивидуальные доли было повседневной практикой (см., например, в библейской книге Чисел стихи 25 – 46 главы 31).

- Другим видом деятельности, приводившим к дробям, были измерения: если, например, стандарт длины не укладывался между двумя данными точками целое число раз, приходилось прибегать к более мелким его частям⁶

Присоединяя к положительным рациональным числам противоположные им величины и ноль, получаем все множество рациональных чисел Q. Оно состоит, таким образом, из нуля, положительных и отрицательных целых чисел, положительных и отрицательных дробей. Сложение, умножение и деление в Q выполняются по формуле (1), вычитание осуществляется по правилу.

(Выполните действия с рациональными числами: ,, -…. )

В множестве Q рациональных чисел все четыре арифметических операции выполняются беспрепятственно за одним досадным исключением: нельзя делить на ноль (один из доводов в пользу того, что 0 –«ненастоящее» число). Следовательно, в этом множестве разрешимы уравнения вида а + х = в при любых а, в и уравнения вида ах = в при всех а0 и при всехв. Таким образом, множество Q является кольцом, а его ненулевые элементы образуют коммутативную группу по умножению. Кольца, обладающие этим свойством, называются полями.

Мы построили поле рациональных чисел (Q⁺,^.). Оно расширяет кольцо целых чисел (Z,⁺,^.), позволяя неограниченно выполнять операцию деления (кроме деления на ноль).

Поле рациональных чисел бесконечно, но существуют и конечные поля. Таковым будет, например, любое кольцо Z_p остатков от деления натуральных чисел на простое число p. Имея перед собой таблицу умножения поля Z₅, легко решить в нем уравнения

2х = 1, 3х = 4, 4х= 5. А вот в кольце Z₆ эти уравнения не имеют корней.

В поле рациональных чисел разрешимо любое уравнение ах + в = 0,решением будет

х = - . Поле рациональных чисел всюду плотно, так как между любыми двумя рациональными числамиr₁ и r₂ можно указать рациональное число (r₁₊ r₂₎:2 и даже бесконечное множество рациональных чисел.

Наглядное представление о рациональных числах дает координатная ось. На некоторой прямой линии выбирается точка 0 – начало отсчета, указывается единица масштаба, направление. Если дано положительное рациональное число ,то единица масштаба делится на n равных частей и вправо от нуля эта доля откладывается m раз. Полученная точка и есть изображение числа . Если число отрицательное – откладывание производят влево от нуля. Например,

-2/3 5/3

-----!--.--.---!--.--.--!--.--.--!--------->

-1 0 1 2

Построив числовое множество Q (поле рациональных чисел), в котором разрешимо любое линейное алгебраическое уравнение ах + в =о, естественно перейти к исследованию квадратных уравнений ах² + вх + с = 0. В простейшем случае х² – 1 = 0, т.е. х² = 1, имеет два решения (корня): х₁ =1, х₂ = -1. Однако уже следующий напрашивающийся шаг заводит нас в тупик.

Теорема 1. Уравнение х² = 2 не имеет решений в поле рациональных чисел.

Теорема 2. Диагональ квадрата несоизмерима с его стороной.

Необходимо самостоятельно познакомиться с доказательствами этих теорем, приводимыми авторами школьных учебников.

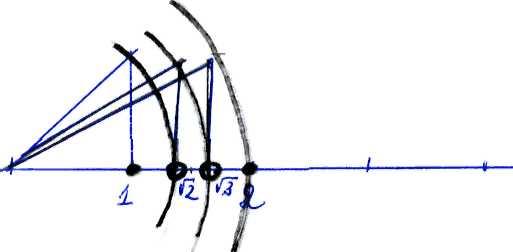
Т

Рис. 1.

еоремы 1 и 2 при всем внешнем несходстве представляют собой лишь разные интерпретации одного и того же математического факта: одна на языке алгебры, другая - в геометрических терминах. (В математике это обычное явление.) Обратимся теперь к координатной оси. Если взять на ней точки, соответствующие рациональным числама и в (пусть а < в), то середина отрезка выражается числомс = (а + в): 2. Это тоже рациональное число, так что между любыми двумя рациональными числами лежит еще одно. Деля пополам отрезки и, получим еще два рациональных числа междуа и в и т.д. Поскольку этот процесс деления пополам (дихотомия) можно продолжать неограниченно, приходим к выводу, что между произвольными рациональными числами а и в находится бесконечно много других рациональных чисел. Представив себе все это, мы могли бы прийти к заключению, что рациональные числа заполняют сплошь числовую ось. Но нет – если от точки 0 отложить вправо диагональ единичного квадрата, то согласно теореме 2 другой конец диагонали не попадет ни в какую рациональную точку. (См. рис. 1) Аналогично строится точка. Вот эти «дыры» на числовой прямой и были интерпретированы как иррациональные числа. (В словаре: «иррациональный – не постигаемый разумом, такой, который не может быть выражен в логических понятиях». Повседневный математический смысл проще: иррациональное число – это число, не являющееся рациональным.)

Иррациональных чисел тоже бесконечно много: если - иррациональное, аа – рациональное число, то сумма а и произведениеа (при а) тоже будет иррациональное число (иначе, например,оказалось бы рациональным).

Первый конкретный пример иррационального числа – это длина диагонали единичного квадрата, т.е. положительный корень уравнения х² = 2, обозначаемый через. Рассуждения, проведенные в доказательстве теоремы 1, могут быть дословно повторены и для уравнений х² = 3, х³ =5, что доказывает иррациональность чисел .

Изобразив действительные числа на координатной прямой, мы получим, что каждой точке координатной прямой соответствует действительное число (прямая без «дырок») и каждому действительному числу отвечает точка на прямой. Координатная прямая, на которой изображено множество действительных чисел, называется числовой прямой, поле действительных чисел стало непрерывным, то есть отношения и алгебраические операции с действительными числами сводятся к одноименным отношениям и операциям с их рациональными приближениями по недостатку и избытку.

После введения действительных чисел появилась возможность дать общую запись для решений любого квадратного уравнения ах² + вх + с = 0 с использованием радикала (знака извлечения корня), а именно х = или х =.

Если величина D = в²- 4ас (дискриминант) положительна, уравнение имеет два корня, рациональных или иррациональных в зависимости от того, является дискриминант полным квадратом или нет.

Золотым сечением называется деление отрезка длины 1 на две части, большая из которых х является средней пропорциональной величиной между всем отрезком и его меньшей частью 1 – х, то есть принцип золотого сечения (название ввел Леонардо да Винчи в конце 15 века) составлял, в частности, теоретическую основу архитектурных композиций классической древности и эпохи Возрождения. Для нахождения х необходимо решить квадратное уравнение х² + х – 1 = 0, откуда х = (отрицательный корень отбрасываем). Для нас иррациональность этого числа очевидна, в древности же она была установлена весьма сложным путем, а сам факт её существования произвел удручающее впечатление.

Пример квадратного уравнения возбудил надежду на то, что алгебраические уравнения и всех других, более высоких степеней, окажутся разрешимыми в радикалах, то есть корни можно будет выразить с помощью арифметических операций и извлечения корней. В середине 16 века итальянские математики Тарталья, Кардано и Феррари нашли подобные формулы для кубического уравнения четвертой степени. (Происходило это в атмосфере ожесточенной полемики о приоритете, с публичными состязаниями в решении соответствующих задач, проклятиями и покаяниями.) В почти три последующие столетия существенных продвижений в этом вопросе не было, и лишь в 1826 году норвежский математик Нильс Хенрик Абель (1802 – 1829) доказал, что для каждого натурального числа n>4 существует алгебраическое уравнение n степени с целыми коэффициентам, неразрешимыми в радикалах (например, х⁵ – 4х – 2 = 0). Окончательное решение проблемы, занимавшей умы лучших математиков, принадлежит французу Эваристу Галуа (1811 – 1832). Он ввел понятие группы и показал, что каждому алгебраическому уравнению соответствует некоторая группа, по свойствам которой и можно судить, разрешимо или нет уравнение в радикалах.

Н. Абель и Э. Галуа ушли из жизни совсем молодыми (первый скончался от туберкулеза, второй был убит на дуэли), их идеи не были должным образом восприняты современниками, но впоследствии оказали огромное влияние на развитие важнейших разделов математики. Имена этих выдающихся ученых носят многие математические объекты, например, абелевыми называются коммутативные группы, а конечные поля – полями Галуа.

Задания к лекции

1. Путь построения числового множества в науке отличается от соответствующего пути, принятого в школьной математике. Укажите эти отличия, вскройте их причины.

2. Проанализируйте методический подход к введению модуля числа, данный в учебниках математики Н.Я. Виленкина. Сравните этот подход с другими, встречающимися в методической и учебной литературе.

3. Познакомьтесь с операциями на множестве Rи разработайте беседу для учащихся 9 класса на тему «Отношения и операции на множестве действительных чисел».

4.Подберите материал и наметьте план беседы для учащихся 9 класса о развитии понятия числа.

Указание1. Большую роль в беседе следует отвести историческим сведениям о развитии понятия числа. 2. Постарайтесь аргументированно обосновать необходимость расширения числовых множеств, показывая при этом потребности практики и науки.

5. Сделайте обзор литературы, которая может быть использована а) учителем для проведения элективного курса по изучению комплексных чисел, б) учеником для самостоятельного чтения при изучении комплексных чисел.