OTIP

	ymax
	B	C* D*
		D
		C	t
	A τ1 τ2 τ3 τ4 τ5
с	графиком	переходной
	Булгакова

Полученная кривая характеризует рост максимально возможного накопленного отклонения в зависимости от времени. Можно сделать вывод: чем больше «колебательность» переходного процесса, тем больше тенденция

к накоплению погрешности.	В подтверждение
сказанному пунктирной линией		на рисунке
представлена кривая накопления,		практически
Рис. 7.1. Кривая накопления	совпадающая

характеристики.

7.5. Расчет вынужденной динамической погрешности при случайных возмущающих воздействиях

В ряде случаев поступающие на входы измерительной системы сигналы представляют собой реализацию случайных процессов, для которых известны математические ожидания и корреляционные функции. Очевидно, на выходе прибора тоже можно получить математические ожидания и корреляционные функции.

Пусть оператор преобразования в расчетной характеристике yр прибора

является интегро-дифференциальным оператором; входной сигнал X (t) является стационарной случайной функцией с математическим ожиданием mx и корреляционной функцией Rx (τ) . Тогда математическое ожидание и корреляционная функция выходного сигнала будут определяться по формулам:

	my =W (0) mx ,	(7.27)
∞	∞
Ry (τ) = ∫h(ξ) ∫h(η)Rx (τ + η− ξ)dηdξ,
−∞	−∞

где h(ξ) – импульсная переходная функция прибора.

Если входной сигнал задан в виде спектральной плотности Sx (ω) , то спектральная плотность выходного сигнала будет

где		W ( jω)		S y (ω) =		W ( jω)		2 Sx (ω),	(7.28)
				– модуль передаточной функции					(амплитудно-частотная

характеристика).

Дисперсия на выходе прибора как суммарная характеристика погрешности будет равна

		1	∞	1	∞		2
	Dy = Ry (0) =		∫S y (ω)dω =		∫	W ( jω)		Sx (ω)dω.	(7.29)
		2π −∞		2π −∞

91

Таким образом, по известным характеристикам входного сигнала mx , Rx (τ) или Sx (ω) можно найти реакцию прибора в виде my , Ry (τ) , Dy , S y (ω) .

Пример 7.3. Для прибора с передаточной функцией

W ( p) = b0 + b1 p a0 + a1 p

найти математическое ожидание my и дисперсию Dy , если на вход прибора

подается сигнал с mx и корреляционной функцией Rx (τ) = Dxe−α τ . Математическое ожидание на выходе согласно (7.27)

	my =W (0) mx =					b0	mx .
						a0
Спектральная плотность на входе прибора
Sx (ω) =	1	∞	Rx (τ)e	− jωτ	dτ =			Dx α
		∫
								π(α2 + ω2 )
	2π −∞

получена с помощью преобразования Фурье корреляционной функции на входе. Квадрат модуля передаточной функции

2

b2

ω2 + b2

W ( jω)

=

1

0

.

a2

ω2 + a2

1

0

Спектральная плотность на выходе в соответствии с (7.28)

D

x

b2

ω2

+ b2

α

S y (ω) =

1

0

.

π a2

ω2

+ a2

α2 + ω2

1

0

Дисперсия сигнала на выходе согласно (7.29)

2D

x

∞

b2

ω2 + b2

α

Dy =

∫

1

0

dω

π

a12 ω2 + a02 α2

+ ω2

0

или после вычисления

a b2

+ αa

b

2

D

= D

1 0

0 1

.

y

x a

)

0

a (αa + a

0

1

1

8. СУММИРОВАНИЕ СОСТАВЛЯЮЩИХ РЕЗУЛЬТИРУЮЩЕЙ ПОГРЕШНОСТИ

8.1. Основы теории расчетного суммирования погрешностей

92

Задача определения расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих называется задачей суммирования погрешностей и возникает во многих случаях в практике измерений.

Для определения погрешности отдельного прибора или измерительного преобразователя необходимо суммировать все составляющие его погрешности (основной, от колебания температуры, от колебания напряжения и др.). При создании измерительных каналов встает задача суммирования погрешностей нескольких измерительных преобразователей, образующих данный измерительный канал. Таким образом, задача расчетного суммирования погрешностей – одна из основных задач как при создании средств измерений, так и при оценке погрешностей результатов самих измерений.

Трудность проведения такого суммирования заключается в том, что все составляющие погрешности должны рассматриваться как случайные величины, принимающие в каждой частной реализации самые разнообразные значения. С точки зрения теории вероятностей они могут быть наиболее полно описаны своими законами распределения, а их совместное действие – соответствующим многомерным законом распределения. Однако в такой постановке задача суммирования погрешностей практически неразрешима уже для 3–4 составляющих (не говоря уже о 30–40), так как операции с многомерными законами непреодолимо сложны. Поэтому практический путь решения задачи суммирования состоит в том, чтобы вместо определения многомерных законов распределения подобрать для характеристики составляющих такие числовые оценки (например, математическое ожидание, СКО, квантильный множитель, энтропийное значение погрешности, энтропийный коэффициент и др.), оперируя с которыми, можно было бы определить соответствующие числовые оценки результирующей погрешности без определения результирующих законов распределения рассматриваемых случайных величин.

При этом необходимо учитывать, что:

1)числовые характеристики законов распределения составляющих могут изменяться в диапазоне изменения измеряемой величины;

2)отдельные составляющие погрешности могут быть коррелированы между собой;

3)при суммировании случайных величин законы их распределения существенно деформируются, т. е. форма закона распределения суммы может резко отличаться от формы закона распределения составляющих.

Правила суммирования погрешностей основываются на предположении

(ограничении), что погрешность по абсолютному значению всегда много меньше самой измеряемой величины. Поэтому изменение погрешности в зависимости от изменения значений самой измеряемой величины может учитываться путем разделения всех суммируемых составляющих погрешности на аддитивные и мультипликативные. Далее предполагается, что сумма аддитивных составляющих дает значение аддитивной части результирующей погрешности, а сумма мультипликативных составляющих – мультипликативной.

93

Впределах диапазона изменения измеряемой величины не более десятикратного изменение результирующей погрешности может быть с достаточной точностью представлено прямой линией. Поэтому достаточно найти значение результирующей погрешности в начале и конце такого диапазона и описать результирующую погрешность линейной двучленной формулой.

При диапазоне изменения измеряемой величины более десятикратного он может быть разбит на участки и результирующая погрешность определена в начале и конце каждого участка.

Для устранения влияния деформации формы законов распределения при суммировании погрешностей все суммируемые составляющие представляются своими СКО σ и все операции расчетного суммирования производятся только над этими средними квадратическими значениями погрешностей.

Учет взаимных корреляционных связей между суммируемыми составляющими производится путем использования различных правил суммирования для жестко коррелированных и слабо коррелированных составляющих.

Врезультате суммирования СКО исходных составляющих получают СКО, соответственно, аддитивной и мультипликативной составляющих результирующей погрешности. Среднее квадратическое отклонение аддитивной составляющей характеризует результирующую погрешность в начале диапазона измерений (при x ≈ 0), а для определения СКО результирующей погрешности в конце диапазона измерений СКО аддитивной и мультипликативной составляющих должны быть просуммированы. Если диапазон измерений простирается на несколько порядков измеряемой величины, то такое суммирование производится

внескольких точках диапазона, а затем принимается решение о методе описания изменения результирующей погрешности во всем диапазоне.

Чаще всего результирующую погрешность желательно выразить не в виде СКО, а в виде энтропийного или доверительного интервала неопределенности.

Этот переход от СКО σ к энтропийному э или доверительному д значениям

погрешности является с теоретической точки зрения самой трудной операцией при суммировании погрешностей. Дело в том, что

э = kΣσΣ	и	д = tΣσΣ ,
где энтропийный коэффициент kΣ	и квантильный множитель tΣ зависят от

формы закона распределения результирующей погрешности, а вся излагаемая методика нацелена на то, чтобы обойтись без точного определения результирующего закона распределения суммы всех составляющих.

Дисперсия суммы коррелированных и некоррелированных случайных величин. Из теории вероятностей известно, что дисперсия суммы двух случайных величин в общем случае

D(x1 + x2 ) = D(x1) + D(x2 ) + 2K x1x2 ,

94

где K x1x2 = kx1x2 σ1σ2 – взаимный корреляционный момент; kx1x2 – коэффициент

корреляции.

Следовательно, СКО суммы этих величин

σ	∑	= σ2	+ 2k	x x		σ σ	2	+ σ2 .
		1			2	1		2
				1

Если случайные величины не коррелированы, то kx1 x2 = 0 и

σΣ = σ12 + σ22 ,

т. е. в подобном случае для определения оценки результирующей погрешности в виде σΣ суммируемые составляющие должны быть оценены также средними

квадратическими отклонениями σ1, σ2 и эти оценки должны суммироваться

геометрически.

Если x1 и x2 жестко и положительно коррелированы ( kx1x2 = +1), т. е. x2

принимает значения, строго пропорциональные x1, то всякое положительное отклонение x1 сопровождается также положительным отклонением x2 и отклонение

(x1 + x2 ) = (x1 ) + (x2 ) .

Это формально следует из формулы для σΣ при kx1x2 = +1, так как

	σ	Σ	= σ2	+ 2σ σ		+ σ2		= σ + σ	2	.
			1	1	2		2	1
Если при возрастании			x1 значения		x2,		наоборот,		линейно убывают, тогда
kx x	= −1 и
1	2

σΣ = σ12 − 2σ1σ2 + σ22 = σ1 − σ2 .

Таким образом, оценки жестко коррелированных погрешностей ( kx1x2 = ±1) должны суммироваться алгебраически с учетом их знаков.

Практические правила расчетного суммирования составляющих результирующей погрешности.

1.В качестве исходных данных задать оценки всех отдельных составляющих погрешности.

2.Для каждой составляющей погрешности найти по исходным данным ее СКО. Для этого необходимо знать вид закона распределения каждой из составляющих.

3.Разделить составляющие погрешности на аддитивные и мультипликативные. (Аддитивные и мультипликативные составляющие суммируются отдельно.)

4.Из суммируемых составляющих выделить группы сильно коррелированных между собой составляющих погрешности, и внутри этих групп выполнить алгебраическое суммирование этих оценок:

95

–если величины положительно коррелированы ( kx1x2 = +1), то σΣ = σ1 + σ2 ;

–если величины отрицательно коррелированы ( kx1x2 = −1), то σΣ = σ1 − σ2 .

Следует заметить, что вычислить точные значения коэффициентов взаимной корреляции составляющих погрешности, как правило, чрезвычайно трудно. Поэтому по степени коррелированности разделяют погрешности на два вида –

сильно	коррелированные	(	kx x	2	[0,7;1]),	и	слабо	коррелированные
			1

( kx1 x2 [0; 0,7]). К первым относят погрешности, вызванные одной и той же

причиной (общим источником питания, одинаковыми изменениями температуры и т. д.), когда тесные корреляционные связи просматриваются логически. Для таких погрешностей принимают kx1x2 = ±1. Погрешности, между которыми такие

взаимосвязи не обнаруживаются, относят к некоррелированным, и для них принимают kx1 x2 = 0.

5. После п. 4 суммарные по группам и оставшиеся вне групп погрешности считают некоррелированными и их складывают геометрически

n

σΣ2 = ∑σi2 .

i=1

Для определения СКО в начале диапазона измерений (при x = 0) суммируют только аддитивные составляющие, в конце диапазона – суммируют все аддитивные и мультипликативные составляющие.

При этом пользуются правилом пренебрежения малыми составляющими при суммировании погрешностей. Можно пренебречь: одной малой составляющей, если она в 5 раз меньше наибольшей из суммируемых составляющих; двумя составляющими, если они в 6 раз меньше; тремя составляющими, если они в 7 раз меньше; четырьмя, если они в 8 раз меньше наибольшей. Применять это правило можно только после суммирования коррелированных составляющих и приведения числовых значений погрешностей к СКО.

6. Выразить	результирующую погрешность в виде энтропийного э		или
доверительного	д интервала неопределенности. Переход к энтропийному		э
или доверительному д интервалу осуществить по формулам:
	э = kΣσΣ и	д = tΣσΣ ,

где kΣ – энтропийный коэффициент, tΣ – квантильный множитель.

7. При определении энтропийного значения погрешности указать соответствующее приближенное значение доверительной вероятности в соответствии с формулой

~	+ 0,1818	ε ≈ 0,899 + κ	2	5,5,	(8.1)
Pд = 0,899

где ε – эксцесс, κ – контрэксцесс. Эксцесс ε определяется по выражению

96

ε = μ4 σ4 ,

где μ4 – четвертый центральный момент, характеризующий протяженность распределения,

μ4 = ∞∫(x − mx )4 p(x)dx .

−∞

Контрэксцесс равен

κ=1 ε .

8.2.Методика расчета энтропийного значения результирующей погрешности

Методика расчета энтропийного значения результирующей погрешности заключается в следующем:

1.Для каждой из составляющих результирующей погрешности найти ее СКО

σi и принять закон распределения вероятностей с известными значениями энтропийного коэффициента ki, эксцесса εi или контрэксцесса κi.

2.Выполнить процедуру суммирования СКО составляющих погрешности:

•для коррелированных составляющих погрешности СКО складываются алгебраически;

•для некоррелированных составляющих погрешности СКО складываются геометрически.

3.Определить энтропийный коэффициент результирующего закона распределения:

•Для жестко коррелированных погрешностей законы распределения каждой из этих погрешностей повторяют форму закона распределения вероятностей вызывающей их общей величины. Сумма жестко коррелированных погрешностей распределена по тому же самому закону, так как мгновенные значения всех ее составляющих совпадают по знаку и пропорциональны друг другу.

Таким образом, при суммировании жестко коррелированных погрешностей деформации законов распределения не происходит, и энтропийный коэффициент распределения суммы равен энтропийному коэффициенту составляющих.

• Задача определения энтропийного коэффициента композиции некоррелированных погрешностей по энтропийным коэффициентам и относительным весам дисперсий каждого из законов распределения в суммарной погрешности достаточно сложна. Ее аналитическое решение известно только для частных случаев суммирования двух нормальных, двух равномерных, и равномерного и нормального распределения.

– При суммировании двух случайных величин, распределенных нормально, их композиция представляет собой также нормальное

97

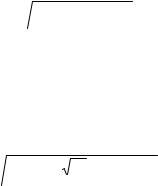
распределение. Поэтому энропийный коэффициент композиции равен энтропийным коэффициентам суммируемых составляющих.

– При суммировании двух равномерно распределенных случайных величин энтропийный коэффициент результирующего распределения

kΣ = 3eC (1 + C2 ) ,

где C = σ1 σ2 при σ1 ≤ σ2 или C = σ2 σ1 при σ2 ≤ σ1 .

– Если одна составляющая погрешности распределена равномерно, а другая – нормально, то строгое решение задачи существенно осложняется. Аппроксимирующее выражение для энтропийного коэффициента такой композиции

kΣ = 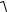3(πe3) pн (1 + pн) ,

где pн = σ2н(σ2р + σ2н ), σр и σн – СКО суммируемых, соответственно,

равномерной и нормальной составляющих.

4. Вычислить энтропийное значение результирующей погрешности по формуле

э = kΣσΣ .

Сводка зависимостей энтропийного коэффициента от соотношения суммируемых составляющих и их энтропийных коэффициентов может быть представлена в виде семейства графиков. Эти зависимости не выражаются аналитическими соотношениями, они получены численным решением для композиций многих видов законов распределений. Результаты решений представлены на рис. 8.1а, б, где по оси абсцисс отложены значения

относительного веса дисперсии второго σ22 из суммируемых распределений в полной дисперсии p = σ22 (σ12 + σ22 ), по оси ординат kΣ – значение энтропийного коэффициента образующейся при этом композиции.

На рис. 8.1а изображены графики значений энтропийных коэффициентов для различных композиций законов распределений:

–горизонтальная прямая 1 соответствует композиции двух нормальных распределений, значение kΣ = 2,066 при любых значениях веса p;

–при суммировании равномерно распределенной погрешности (k = 1,73) с нормально распределенной (k = 2,066) изменение kΣ соответствует кривой 2;

98

а)

б)

Рис. 8.1. Сводка зависимостей энтропийного коэффициента от соотношения суммируемых составляющих

– если суммируемые погрешности распределены равномерно, то изменение kΣ соответствует кривой 3, которая начинается при p = 0 и kΣ =1,73 , достигает

максимума при p = 0,5 и kΣ = 2,02 , заканчивается при p = 1 и kΣ =1,73 ;

– при суммировании арксинусоидально распределенной составляющей и равномерно распределенной составляющей погрешностей изменение kΣ

99

соответствует кривой 4, которая начинается при p = 0 и kΣ =1,11, достигает максимума kΣ =1,98 и заканчивается при p = 1 и kΣ =1,73 ;

– при суммировании двух арксинусоидально распределенных погрешностей kΣ изменяется согласно кривой 5 от kΣ =1,11 при p = 0 до kΣ =1,88 при p = 0,5 и

далее вновь убывает до kΣ =1,11 при p = 1. На рис. 8.1б:

–кривая 1 соответствует суммированию равномерного с дискретным двузначным распределением;

–кривая 2 – суммированию треугольного с дискретным двузначным распределением;

–кривая 3 – суммированию нормального с дискретным двузначным распределением;

–кривая 4 – суммированию нормального с арксинусоидальным распределением;

–кривая 5 – суммированию нормального с равномерным распределением;

–кривая 6 – суммированию нормального с экспоненциальным распределением.

Несмотря на то, что кривые рис. 8.1а, б построены только для нескольких видов законов распределения, их сетка настолько густа, что позволяет на глаз интерполировать значения kΣ для композиций любых законов распределения с

известными энтропийными коэффициентами.

Однако при расчете суммарной погрешности на компьютере предпочтительнее использовать вместо значений, взятых с рис. 8.1а, б, приближенные формулы, аппроксимирующие эти кривые. Так семейство симметричных кривых 1, 3, 5 (см. рис. 8.1а) с погрешностью 1,5 % при k ≥1,8 и с погрешностью 2,5 % при

1,11 ≤ k <1,8 описывается соотношением

kΣ = k +1,15(kн − k)0,75[p(1 − p)]0,21k1,15 ,

где k – энтропийный коэффициент суммируемых составляющих; p и (1 – p) – веса суммируемых составляющих; kн = πe2 = 2,066 – энтропийный коэффициент

нормального распределения.

Несимметричные кривые вида кривой 4 (см. рис. 8.1а), начинающиеся при k = k1 и оканчивающиеся при k = k2 , где k1 < k2 , с погрешностью 2 %

описываются соотношением

k

Σ

= k + (k

2

− k )[p + a

0

pa1 (1 − p)a2 ],

1

1

где p – вес составляющей с k = k1 ; (1 – p) – вес составляющей с k = k2 ;

a

0

= 0,817(1 + k

k

2

) ;

a

= 0,75(k

k

2

)4,5

;

a

2

=1,23(k

k

2

)2 .

1

1

1

1

Несимметричные

кривые

вида

кривой

2

(см. рис. 8.1а) и кривых 4–6

(см. рис. 8.1б) для

суммирования

нормально

распределенных погрешностей

с погрешностями,

распределенными

с

энтропийным

коэффициентом k,

100