OTIP

где A – экваториальный момент инерции шарового ротора; H – кинетический момент гироскопа в собственном вращении; b – коэффициент сопротивления вращению в гидроподвесе; k1, k2 – коэффициенты электромагнитных моментов, характеризующих взаимодействие намагниченного ротора с электрическими

обмотками статора;	гидр	,	гидр	–	проекции возмущающих моментов со
	M Oy1		M Oy 2
стороны гидроподвеса на оси Резаля;					~	,	~	– проекции возмущающих
					MOy1		MOy2

моментов, обусловленных другими факторами; ζ1, ζ2, ζ3 – оси, связанные с платформой; ωζ1, ωζ2 – составляющие угловой скорости платформы; α, β – углы

поворота гироскопа относительно платформы.

При позиционной цепи стабилизации электромагнитные моменты двигателя вызывают дрейф платформы гиростабилизатора. Введением интегральнопозиционной цепи стабилизации влияние этих моментов на дрейф платформы в установившемся режиме ( α = 0 , β = 0) исключается. Тогда основными возмущающими моментами становятся гидродинамические моменты, обусловленные инструментальными погрешностями изготовления и сборки каркаса статора. Является актуальной задача оценки этих моментов и результирующих гидродинамических сил, приложенных к ротору гироскопа.

10.1. Постановка задачи

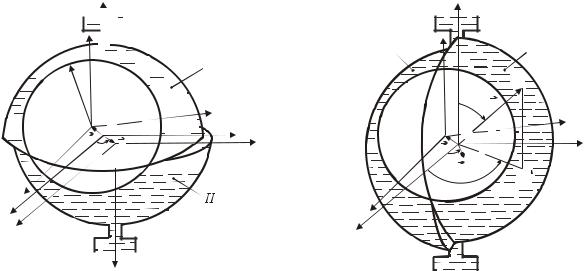
Шаровой ротор выполняет установившееся вращение с угловой скоростью ω вокруг горизонтальной оси в неподвижной полости статора. Каркас статора составлен из двух полусферических сегментов. Предполагается, что отклонения главной оси ротора Oz3 относительно оси статора Ox x3 малы и ими можно пренебречь при определении реакций подвеса. Исследуются схемы гидродинамических подвесов с учетом геометрических погрешностей в виде усечения и сдвига центров сегментов: в схеме А плоскость смещения усеченных сферических сегментов, составляющих статор, перпендикулярна оси вращения ротора (рис. 10.2а); в схеме В вектор сдвига центров оснований сегментов лежит в плоскости, проходящей через ось вращения ротора (рис. 10.2б). Геометрические параметры отверстий таковы, что они не являются ограничителями расхода поступающей в зазор жидкости.

161

x 3 , x 3I

А

z 3

I

R 2

z 2

О

Оx

, Оx

I

x 2 , x 2

I

x 1II

e

φ

χ

II

Оx

z 1
x 1 , x 1I
x 2	Б
	x II3

		3
II	z 3			А	I
		θ			M
				r	z 2
	О
		О	,	I	x	2
		x		Оx
	eφ χОIIx				M
	ϕ
z 1
x 1			Б

а) схема А

б) схема В

Рис. 10. 2. Расчетные схемы гидродинамического подвеса

Течение тонкого слоя ньютоновской несжимаемой жидкости в зазоре подвеса изучается в соответствии с классическими допущениями гидродинамической теории смазки: режим течения жидкости принимается ламинарным и изотермическим, жидкость рассматривается как сплошная безинерционная среда с динамическим коэффициентом вязкости, не зависящим от давления. При таких допущениях уравнение для распределения давления в слое жидкости принимает вид уравнения Рейнольдса.

10.2. Определение реакций гидроподвеса для расчетной схемы А

В случае схемы А (см. рис. 10.2а) пространство между статором и ротором разделим на две области, граничащие в плоскости экватора (плоскости сдвига): область I соответствует сегменту I, область II – сегменту II. Введем системы

координат (СК): связанную со статором Oxi , связанные с сегментами Ox(k ) xi(k ) (k = I, II), полюсы Ox(k ) расположены в центрах оснований сегментов. Принимаем,

162

что координатные оси Oxi и OxI xiI

Рис. 10.3. Системы координат

Рис. 10.4. Усечение полусферы I вдоль оси x3I

где

совпадают. Величины, относящиеся к областям I и II, запишем с индексами I и II соответственно. Сферические координаты r, θ, ϕ отсчитываем, как показано на рис. 10.3: в области I

в СКx I	(r	[0, RI ],	θ [0, π/2],
i		1
ϕ [0, 2π]);	в	области	II – в СКxiII

(r [0, R1II ], θ [0, π/2], ϕ [0, 2π]).

Уравнения поверхностей I и II статора в СКxi(k ) приближенно записываются в виде R1(k ) = R1 − χ3(k ) cosθ,

где R1 – радиус сферы статора; χ3(k ) – усечение k-той полусферы вдоль оси

x3(k) (рис. 10.4).

Положение центра О ротора в СКxi(k ) определяется вектором er(k ) . В

области k относительная величина зазора в радиальном направлении с теми же приближениями записывается

в виде

5

H (k ) =1 − ∑λ(ik ) Hi(k ) , i=1

λI1 = λII2 = ε1 ; λI2 = λII1

= ε2 ; λI3 = λII4

=

1; λI4 = λII3

=

2 ;

(10.1)

χ

χ

λI5 = ε3 +

3I ;

λII5

= −ε3 +

3II ;

(10.2)

χ

χ

εi = exi(k ) /δ

(i =

) – безразмерные значения проекций вектора смещения e

на

1, 3

оси Ox

i

; δ = R1 – R2; χ(k ) = χ(k)

δ,

χ = χcos φ, χ

2

= χsin φ

, χ = χ δ,

χ =

O IO II

–

3

3

1

x

x

модуль вектора сдвига центров сегментов I и II, φ – угол ориентации вектора

сдвига

χ

(см. рис. 10.2а, 10.3);

H1I = H2II = sin θcosϕ,

H2I

= H1II = sin θsin ϕ,

H3I = H4I = 0, H3II

= −sin θcos ϕ,

H4II = −sin θsin ϕ,

H5I = H5II = cos θ.

Величины λ(ik )

(i =

), определяемые относительными смещениями центра

1, 5

ротора

εj

( j =

)

и

погрешностями

геометрии

3I ,

3II ,

,

могут

1, 3

χ

χ

χ

рассматриваться как малые параметры.

163

Течение жидкости в зазоре подвеса описывается уравнениями Рейнольдса. Рассматривая эти уравнения совместно с уравнением неразрывности и используя краевые условия «прилипания» для скоростей, получим дифференциальное уравнение для распределения давления:

∂

∂

(k )

∂

∂

(k )

p

p

sin θ

(H (k ) )3 sin θ

+

(H (k ) )3

=

∂θ

∂θ

∂ϕ

∂ϕ

= −l(k )Λsin3 θ((λ(2k ) − λ(4k )ν(k ) )cosϕ − (λ(1k ) − λ(3k )ν(k ) )sinϕ),

(10.3)

где p(k ) – безразмерное давление в области k; p(k ) = p(k ) po ; po – давление в

камере; l I =1	; l II = −1	; νI = 0, νII =1; Λ = 6μωR2	(δ2 p ) .
		2	o

При постановке краевой задачи для распределения давления принимаем следующие условия:

•давление является непрерывной функцией координат θ, ϕ и периодической функцией с периодом 2π по координате ϕ: p(k )(θ,ϕ) = p(k )(θ,ϕ + 2π);

•жидкость непрерывно заполняет зазор;

•отверстия не являются ограничителями расхода, поэтому давление под отверстиями А и Б принимается равным давлению в камере;

•на границе областей I и II выполняются условия непрерывности давления и местных меридиональных расходов.

Тогда краевые условия для функций p(k )(θ,ϕ) записываются в виде:

(k )

*

p

(θ1,ϕ)

=1,

θ1 = r

R1 ,

I

II

p

(π/ 2,ϕ)

= p

(π/ 2,ϕ),

(10.4)

[(H I )3 ∂

I

∂θ]θ=π 2 = −[(H II )3 ∂

II

∂θ]θ=π 2

,

p

p

где r* – радиус отверстия.

Функцию давления приближенно представим в виде линейной части простого разложения в ряд по степеням малых параметров λ(ik ) :

p(k ) = Po(k ) + ∑5 λ(ik ) Pi(k ) . i=1

Функции первого приближения приводятся к виду:

Po(k ) =1,

Pi(k ) = li(k ) X i(k ) sin ϕ +Yi(k ) Pj(k ) =Y j(k ) sin ϕ − l(jk ) X (jk )

P5(k ) = 0.

cosϕ	(i =1, 3;	l I	=	l II	=1,	l II	=	l I	= −1),
		1		3		1		3
cosϕ	( j = 2, 4;	l2I	= l4II		=1,	l2II	=	l4I
									= −1),

164

Функции X m(k ) = X m(k ) (θ), Ym(k ) = Ym(k ) (θ) (m =1, 4; k = I, II ) находятся решением восьми краевых задач вида:

где Z =

ν(k )

X1

d

I

sin θ

(sin θ

dZi

) − ZiI

= νZI i Λsin2 θ;

dθ

dθ

d

sin θ

dZiII+1

sin θ

− Z II

= νII

Λsin2

θ;

dθ

dθ

i+1

Zi+1

при θ = θ1 :

ZiI = ZiII+1 = 0;

при θ = π/ 2 :

ZiI

= ZiII+1;

dZiI

dθ = −dZiII+1

dθ;

d

I

sin θ

(sin θ

dZi+1

) − ZiI+1 = νZI

Λsin2 θ;

dθ

dθ

i+1

d

dZ II

) − ZiII

= νZIIi Λsin2 θ;

sin θ

(sin θ

i

dθ

dθ

= Z II = 0;

при θ = θ :

Z I

1

i+1

i

при θ = π/ 2 :

I

II

;

I

II

Zi +1 = Zi

−dZi+1 dθ = dZi

dθ,

X , Y ;

i = 1, 3;

= ν(k )

= νII

= νII

=1,

νI

= νI

= ν(k ) = 0;

k = I, II; j =

.

1, 4

X 2

X

3

X 4

X 3

X 4

Y j

(10.5)

(10.6)

Применение метода малых возмущений позволило свести решение двумерной краевой задачи (10.3), (10.4) к восьми краевым задачам для обыкновенных дифференциальных уравнений второго порядка (10.5), (10.6), которые решаются численным методом. Строятся разностные схемы интегроинтерполяционным методом на равномерной сетке. Разностные уравнения приводятся к системам линейных алгебраических уравнений трехдиагональной структуры, которые решаются методом прогонки. По известным значениям функций

X m(k ) , Ym(k ) (m =											(k ) в области k
			1,	4; k = I, II ) находится распределение давления						p
		(k ) =1 + λ(k )(l(k ) X (k )				sin ϕ +Y (k ) cosϕ) + λ(k )(Y (k ) sin ϕ − l(k ) X (k ) cosϕ) +
	p
		1		1		1	2	2	2
		+ λ(k )( − l(k ) X (k ) sinϕ +Y (k ) cosϕ) + λ(k )(Y (k ) sinϕ + l(k ) X (k ) cosϕ)										(10.7)
		3		3		3	4	4	4

(lI = 1, lII = –1).

Рассматривая напряжения жидкости на поверхности ротора, определим в соответствии с принятыми приближениями проекции на оси Oxi статора главного

вектора F (k ) и проекции главного момента гидродинамических сил M O(k ) в k-той области. Результирующие гидродинамическая реакция подвеса F и момент реакций подвеса M O соответственно равны:

F = F I + F II ; M O = M OI + M OII .

165

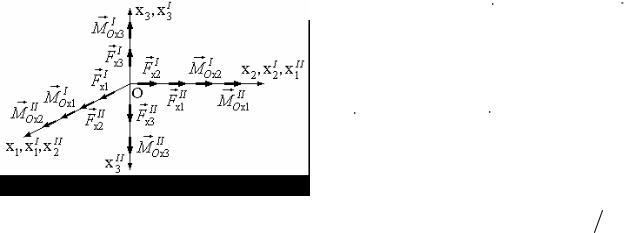
Проекции силы					F и момента M O
на оси		СКxi			статора находим
согласно рис. 10.5:
	F I	+ F II				M I	+ M II
	x1	x2				Ox1	Ox2
F =	F I	+ F II		;	M O =	M I	+ M II				.
	x2	x1				Ox2	Ox1
	F I	− F II				M I	− M II
	x3	x3				Ox3	Ox3

			Введя масштабные коэффициенты
Рис. 10.5. К определению реакций подвеса				KF = πpo R22 , KМ = πμω R24 δ,
			запишем значения сил и моментов
Fxi = KF		xi , MOxi	= KM		Oxi (i =		).
	F			M		1, 3

Соответствующие безразмерные величины определяются в виде интегралов:

		π/ 2
F	x1 = − ∫[ − ε2 ( X2I		+ X1II ) +			χ	sin φ( X 4I + X3II )]sin2 θdθ;
		0
		π/ 2
F	x2	= − ∫[ε1( X1I +	X 2II ) −	χ	cosφ( X3I + X 4II )]sin2 θdθ;				(10.8)
		0
F	x3	= 0.

π/

2

I

II

− X II )cosθ

Ox1 = 1

cosφ+

3

{ε

(dX1

− dX2

)sin θ + ( X I

−

M

χ

∫

4

Λ

1

dθ

dθ

1

2

0

I

II

−

cosφ (dX3

− dX4 )sin θ + ( X I

− X II )cosθ }dθ;

χ

dθ

dθ

3

4

π/ 2

I

II

Ox2 = 1

sin φ+

3

{ε

(dX2

−

dX1

)sin θ + ( X I

− X II )cosθ

−

(10.9)

M

χ

∫

2

4

Λ

dθ

dθ

2

1

0

I

II

−

sin φ (dX4

− dX3 )sin θ + ( X I

− X II )cosθ }dθ;

χ

dθ

dθ

4

3

= −8 −

1

M Ox3

(χ3I

+ χ3II ).

3

2

Величины MOx1 ,

M Ox2

представляют возмущающие моменты для гироскопа,

величина MOx3 – момент сопротивления его быстрому собственному вращению.

Интегралы безразмерных проекций гидродинамических сил и моментов вычисляются с помощью квадратурной формулы Симпсона.

166

10.3. Определение гидродинамических реакций подвеса для расчетной схемы В

В расчетной схеме В гидродинамического подвеса (см. рис. 10.2б) учитываются производственно-технологические погрешности в виде усечения и

смещения деталей статора, вектор сдвига центров сегментов χ лежит в плоскости, проходящей через ось вращения ротора.

Пространство между статором и ротором разделим на две области: область I соответствует сегменту I, в ней r [0, R1I ], θ [0, π], ϕ [0, π]; область II – сегменту II, в ней r [0, R1II ], θ [0, π], ϕ [π, 2π]. Все величины, относящиеся

к этим областям, будем записывать с индексами I и II соответственно. Поверхности I и II в СКxi статора описываются уравнениями:

R1I = R1 − χ2I sin θsin ϕ,
RII = R		− χII sin θsin ϕ − ϕ(cosφsin θcosϕ + sin φcosθ),
1	1	2

где R1 – радиус идеальной сферы статора; χ – модуль вектора сдвига центров сегментов I и II; φ – угол ориентации вектора сдвига χ (угол между осью Oxx1 и вектором χ) (см. рис. 10.2б); χ(2k ) – усечение полусферы k вдоль оси x2(k ) , k = I, II; на рис. 10.6 показано усечение полусферы I вдоль оси x2.

Положение центра ротора О в СКxi

статора определяется вектором e . В области k относительная величина зазора в радиальном направлении записывается в виде

Рис. 10.6. Усечение полусферы I

вдоль оси x2I

оси Oxi ; δ = R1 – R2; χ2(k ) = χ(2k ) δ,

H

(k ) =1 − ε(k )

sin θcosϕ −

1

− ε(2k ) sin θsin ϕ− ε3(k ) cos θ,

где

εI

= ε ; εII

= ε

+ χcos φ;

εI

= ε

2

+ χI ; (10.10)

1

1

1

1

2

2

ε2II

= ε2 −χ2II ; ε3I

= ε3 ; ε3II

= ε3 + χsin φ; (10.11)

ε(k ) = e(k )

δ (i =

) –

безразмерные зна-

1, 3

i

i

чения

проекций

вектора

смещения e на

χ = χ δ,

χ =

O xIO xII

– модуль вектора сдвига

центров сегментов I и II, φ – угол ориентации вектора сдвига χ (см. рис. 10.2б).

Дифференциальное уравнение для распределения давления слоя жидкости получено также, как и для схемы А:

167

∂

∂

(k )

1 ∂

∂

(k )

p

(H (k ) )3

p

(H (k ) )3

sin θ

∂θ

+

∂ϕ

=

∂θ

sin θ ∂ϕ

		= Λsin2 θ(ε(k ) sin ϕ − ε(k ) cosϕ) (k = I, II), (10.12)
1			2
где		(k ) – безразмерное давление в области k,		(k ) = p(k ) /po ; po – давление в
	p		p

камере; Λ = 6μωR22 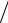(δ2 po ) .

При постановке краевой задачи для распределения давления учитываются те же допущения, что и для схемы А. Краевые условия записываются в виде:

(k )(θ ,ϕ) = 1,

I

(θ, 0) =

II

(θ, 0),

I (θ, π) =

II (θ, π),

(10.13)

p

p

p

p

p

1

где θ1 = r* / R1 (r* – радиус отверстия).

Уравнению в частных производных можно поставить в соответствие систему алгебраических уравнений относительно значений функции в выбранных узлах области Ω решения краевой задачи разными методами. Дискретизация чаще всего осуществляется с помощью метода конечных разностей и метода конечных элементов.

В рассматриваемой схеме зазор терпит разрыв по координате ϕ с переменной по координате θ «ступенькой». Учесть нерегулярности геометрии зазора гидродинамического подвеса позволяет метод конечных элементов (МКЭ). Элементы могут аппроксимировать границы любой конфигурации. Использование интерполяционных функций, обеспечивающих непрерывность давления и массового расхода, дает возможность проводить анализ ступенчатых конфигураций.

Для решения представленной двумерной краевой задачи (10.12), (10.13) применяется МКЭ в формулировке Галеркина. Уравнение (10.12) переписываем в дивергентной форме:

(k )

L(

p

(k ) ) =

∂

sin θ∂p

(H (k ) )3

+

∂θ

∂θ

(k )

∂

1 ∂p

+

(H (k ) )3 + Λsin2

θ(ε(k ) cosϕ + ε(k ) sin ϕ)

= 0, (10.14)

∂ϕ sin θ

∂ϕ

1

2

где L( )

– дифференциальный оператор.

Поверхность чаши подвеса разбивается на четырехугольные конечные элементы N параллелями и L меридианами по сферическим координатам θ, ϕ соответственно. Причем, линии координатной сетки, проходящие по меридианам ϕ = 0 и ϕ = π через полюсы сферы θ = 0, θ = π, разделяют поверхность на области

I и II, (см. рис. 10.2б).

Приближенное решение краевой задачи (10.13), (10.14) записывается в виде линейной комбинации пробных функций, коэффициентами которых являются

узловые значения искомой функции давления в области k (k = I, II)

168

~(k )	M N			(k )	,	(10.15)
P	= ∑∑ϖi j (θ,ϕ) pi j
	j=1i=1
где ϖi j(θ,ϕ) – двумерные	билинейные	пробные функции;					i(kj ) – значения
						p

функции давления в узлах (i j), которым соответствуют координаты θi и ϕj в области k.

На каждом из элементов, примыкающем к узлу (i j), определяем пробные функции ϖi j (θ,ϕ) . Для этого в каждом конечном элементе вводим локальную

нумерацию узлов (рис. 10.7) и локальные координаты λ, ν ( −1 ≤ λ ≤1, −1 ≤ ν ≤1).

Локальные координаты связаны с глобаль-

	ными следующими соотношениями:
	внутри элементов A, B
	λ = 2[ϕ – (ϕj+1 + ϕj)/2]/Δϕ;
	внутри элементов С, D
	λ = 2[ϕ – (ϕj–1 + ϕj)/2]/Δϕ;
	внутри элементов A, D
Рис. 10.7. Глобальная и	ν = 2[θ – (θi+1 + θi)/2]/Δθ;
локальная нумерация узлов	внутри элементов B, C
	ν = 2[θ – (θi–1 + θi)/2]/Δθ.

Билинейные пробные функции в локальной системе координат заданы формулами:

ϖu (λ,ν) = 0,25(1+ ς1u λ)(1+ ς2u ν),

где u = 1, 4 ; ς11 = ς14 = ς21 = ς22 = – 1, ς12 = ς13 = ς23 = ς24 = 1.

Приведенные аппроксимирующие функции обладают следующими

интерполяционными свойствами:
ϖu (λ, ν) =1, если λ = λu , ν = νu	(u =
		1, 4);		(10.16)
ϖu (λ, ν) = 0 для другихслучаев.
Здесь ϖ u (λ,ν) – значение функции в локальном узле u;				λu, νu – значения
локальных координат λ, ν в узле u.

Для представления приближенного решения (10.15) в матричной форме вводится сквозная нумерация узлов сетки: узлу (i j) соответствует новый узел с номером t, причем t = M(i −1) + j .

Так как i =1, N и j =1, M , то индекс t принимает значения t =1, N × M .

Следовательно,	пробные функции и узловые значения функции давления
принимают вид
	~	~(k )			(k )	.
	ϖt (θ,ϕ) = ϖi j (θ,ϕ) ;	pt	= pi j

Тогда приближенное решение (10.15) в области k представим в виде

169

~(k )

= W P

(k )

,

(10.17)

P

где W – матрица-строка, компонентами которой являются билинейные пробные

~

(k)

– столбец искомых узловых значений функции давления

функции ϖt

(θ,ϕ) ; P

~(k )

в области k; t =1, N × M .

pt

После подстановки приближенного решения (10.17) в уравнение (10.14)

получаем невязку (k)

в области k

(k ) = L(P~(k ) ) .

С целью определения значений

~(k )

потребуем, чтобы интеграл взвешенной

pt

невязки по всей вычислительной области Ω(k) был равен нулю

~

(k )

dϕdθ = 0

( m =1, N × M ) ,

(10.18)

∫∫ϖm(θ,ϕ)

~

Ω( k )

– весовая функция, которая согласно методу Галеркина выбирается

где ϖm (θ,ϕ)

~

из того же семейства, что и пробные функции ϖt (θ,ϕ) ; m – параметр,

соответствующий всем номерам t узлов сетки (t =

).

1, N × M

В равенство (10.18) подставляем невязку:

~

∂Θ(θ,ϕ)

~

∂Φ(θ,ϕ)

(10.19)

∫∫

ϖm (θ,ϕ)

∂θ

+ ϖm (θ,ϕ)

∂ϕ

dϕdθ = 0.

Ω( k )

Здесь использованы обозначения:

Θ(θ,ϕ) = sin θ(H (k ) )3

∂

(W P(k ) ),

∂θ

(10.20)

(H (k ) )3 ∂

(k )

2

(k )

(k )

(W P

Φ(θ,ϕ) =

) + Λsin

θ(ε1

cosϕ + ε2

sin ϕ).

sin θ

∂ϕ

Запишем полученное интегральное соотношение (10.19) в эквивалентном виде

~

Θ)

~

Φ)

~

~

∫∫

∂(ϖ

m

+

∂(ϖ

m

∂ϖ

m + Φ

∂ϖ

m

(10.21)

dϕdθ−

∫∫ Θ

dϕdθ = 0 .

Ω( k )

∂θ

∂ϕ

Ω( k )

∂θ

∂ϕ

Первый интеграл в (10.21) преобразуем по формуле Грина:

~

Θ)

~

~

~

∫∫

∂(ϖm

−

∂(−ϖmΦ)

(10.22)

∂θ

∂ϕ

dϕdθ = ∫

(ϖmΘdϕ − ϖmΦdθ) = 0 ,

Ω( k )

L( k )

где L(k) – граница области Ω(k). Криволинейный интеграл берется по контуру L(k), пробегаемому в положительном направлении.

Следовательно, выражение (10.21), записанное с учетом (10.22) и обозначений (10.20), принимает вид

~

∂

~

(H

(k )

)

3

∂

∂ϖm

sin θ(H

(k )

)

3

(W P

(k )

)

+

∂ϖm

(W P

(k )

∫∫

∂θ

∂θ

∂ϕ

sin θ

∂ϕ

) dϕdθ =

Ω( k )

~

= − ∫∫

∂ϖ

m Λsin2 θ(ε1(k ) cosϕ + ε(2k ) sin ϕ) dϕdθ

Ω( k )

∂ϕ

170