OTIP

Проекция отрезка ОD на направление Оу дает величину ОЕ, представляющую собой погрешность положения толкателя, вызванную перекосом оси кулачка:

yγ =		OD		π		(5.28)
				cos	− ψγ .
				2
Записывая выражение (5.28) с учетом (5.27), получим
yγ = b				γsin ψγ .
2

Введем входное воздействие α. При повороте оси кулачка на угол α верхний торец коснется толкателя при условии 0 ≤ α + ψγ ≤ π. При выходе угла α + ψγ за

эти пределы вступит в действие нижний торец кулачка. Изменение функции
yγ (α) в зависимости от угла α показано на рис. 5.16.
			yγ			yγI	yγII
							α
								Рис. 5.16. Изменение частной погрешности
			ψγ
								yγ в зависимости от угла α

Сплошная линия соответствует касанию верхнего торца с толкателем, пунктирная – нижнего торца. Практически касание возможно только при положительных значениях yγ , поэтому выражение для функции частной

погрешности будет иметь вид

yγ = b	γ		sin(α + ψγ )		.
2

6.ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ ПОГРЕШНОСТЕЙ

6.1.Необходимые сведения из теории вероятностей

Погрешности измерительных приборов носят случайный характер. Случайность обуславливается: случайным характером измеряемой физической величины, непостоянством метрологических характеристик измерительных приборов, а также случайным характером воздействия внешних факторов на измерительный прибор в процессе измерения. Учет только детерминированных значений погрешностей дает ограниченную и в большинстве случаев недостаточную информацию. Поэтому погрешности показаний измерительных приборов, как и первичные погрешности, будем рассматривать как случайные величины.

61

Случайными величинами называются такие величины, которые при неоднократном повторении опыта в неизменных условиях принимают каждый раз новые значения. При изготовлении партии измерительных приборов по одному проекту погрешности показаний отдельных экземпляров будут отличаться друг от друга. При многократном испытании одного экземпляра прибора получают также ряд случайных результатов.

Законы распределения случайной величины. Основными характеристиками случайной величины X являются интегральный и дифференциальный законы ее распределения.

Интегральным законом или функцией распределения F(x) случайной величины

X называют вероятность того, что случайная величина X меньше заданной величины x

F(x) = P{X < x}.

F(x) – неубывающая функция x, изменяющаяся от F(−∞) = 0 до F(+∞) =1. Она существует для всех случайных величин, как дискретных, так и непрерывных.

Для случайной величины с непрерывной и дифференцируемой функцией распределения F(x) можно найти дифференциальный закон распределения или

плотность распределения вероятностей p(x): p(x) = d F (x)dx .

Плотность распределения вероятностей p(x) всегда неотрицательна и подчинена условию нормирования в виде

+∞

∫ p(x) dx =1,

−∞

что непосредственно следует из свойств функции распределения F(x). Вероятность попадания случайной величины X на интервал [a, b] определяется

по формуле

b

P{a < X < b}= F(b) − F(a) = ∫ p(x) dx .

a

Примеры законов распределения. Наиболее часто встречаются законы распределения (рис. 6.1): нормальный, равномерный, Симпсона, симметричный экспоненциальный и трапецеидальный.

1

p(x)

p(x)

p(x)

p(x)

p(x)

1/(b2-b1)

1/a

σ

2π

x

x

x

x

x

0

m

0

b1

b2

0

m-a m m+ a

0

0

а)

б)

в)

г)

д)

Рис. 6.1. Законы распределения: а – нормальный, б – равномерный, в – Симпсона,

62

г – симметричный экспоненциальный, д – трапецеидальный

Для нормального закона распределения (см. рис. 6.1а) характерны следующие закономерности: равные по абсолютному значению погрешности равновероятны; малые погрешности более вероятны, чем большие. Плотность распределения для нормального закона

	p(x) =	1		(x − m)2
			exp −	2σ2		,
		σ 2π
	где m – математическое ожидание погрешности; σ2				– дисперсия погрешности.

По нормальному закону распределены многие погрешности, поэтому в инженерной практике это распределение чаще всего используется, иногда без достаточного основания.

Плотность вероятности равномерного закона (см. рис. 6.1б)

1	(b	− b )	при b	< x	< b		;
p(x) =	2	1	1	< b1	2			> b2 .
0			при x		и	x

По равномерному закону распределены погрешности: от трения в опорах; от округления; отсчета; от порога нечувствительности и др.

Плотность распределения треугольного закона Симпсона (см. рис. 6.1в) можно представить в виде

	x − m + a
		a	2
		− x + m + a
	p(x) =
		a2
	0

при m − a < x < m;

при m < x < m + a;

при x < m − a и x > m + a.

По этому закону распределены погрешности: суммарная при измерении длин; суммарная от квантования интервала времени при равномерном законе

	распределения ее двух составляющих и др.
	Плотность распределения симметричного экспоненциального закона
	p(x) =	α	exp(−		x		α ),	(6.1)
		2 Г(1 α)

где Г(1α) – гипергеометрическая функция; α – число, которое может принимать

значения от 0 до ∞. При α → ∞ получаем равномерный закон вида, изображенного на рис. 6.1б; при α > 2 получаем плавные законы, близкие к трапецеидальным (см. рис. 6.1д); при α = 2 имеем нормальный закон (см. рис. 6.1а) и, наконец, при α = 1 и α = 0,5 выражение (6.1) принимает соответственно вид

p(x) =	1 e−		x		и	p(x) =	1 e−		x		1 4 .
	2						4

Графическое изображение этих законов показано на рис. 6.1г.

63

По законам, близким к

p(x) = e− x2 ,

распределяются редкие случайные события, например, выбросы случайных процессов за установленную границу.

Распределение отсчетов синусоидально изменяющейся во времени величины x = X m sin ωt , если моменты этих отсчетов равномерно распределены во времени,

называется арксинусоидальным. Его плотность описывается выражением

p(x)

p(x)

p(x) =1 (π X m2 − x2 )

и представлена на рис.6.2а.

Распределение, при

кото-

ром встречаются

с равными

вероятностями

только

два

-Xm

0

X

m

-a

0

a

дискретных значения случай-

Рис. 6.2. Законы распределения:

ной величины

+a и –a,

а – арксинусоидальный,

называется

дискретным

б – дискретный двузначный

двузначным распределением.

Его плотность распределения

вероятностей представлена на рис. 6.2б и описывается аналитически

p(x) =

1 δ(x − a) +

1

δ(x + a) ,

2

2

где δ – дельта-функция Дирака.

Числовые характеристики случайной величины. При решении многих прикладных задач вместо законов распределения вероятностей случайной величины пользуются числовыми характеристиками, к которым в том числе относятся:

– математическое ожидание случайной величины

∞

mx = ∫ x p(x)dx ,

−∞

которое можно рассматривать как среднее взвешенное из всех возможных значений случайной величины X, где в качестве веса используется плотность распределения;

– дисперсия случайной величины

Dx = ∞∫(x − mx )2 p(x)dx ,

−∞

характеризующая разброс фактических значений случайной величины относительно ее математического ожидания;

– среднее квадратическое отклонение (СКО) случайной величины есть положительное значение квадратного корня из ее дисперсии

σx = Dx .

64

Использование дисперсии на практике не всегда удобно, так как ее размерность есть квадрат размерности случайной величины. Поэтому для более наглядной характеристики рассеяния пользуются средним квадратическим отклонением, имеющем размерность самой случайной величины.

Можно определить характеристики случайной величины на основании обработки опытного материала. Из статистики известно, что обработка экспериментальных данных не позволяет определить точные значения математического ожидания и дисперсии, а дает возможность найти только их приближенные значения – оценки искомых параметров.

Пусть в результате n независимых испытаний получено n значений величины x, которые обозначим

x1, x2, …, xk , …, xn.

(6.2)

Реализация (6.2) называется выборкой из генеральной совокупности, n – объем выборки, xk – элементы выборки.

Оценка

~

математического ожидания mx определяется как среднее

mx

арифметическое элементов выборки (6.2)

~

=

1

n

mx

∑xk .

~

n k =1

Дисперсия оценки mx определяется формулой

~

] =

1

~

2

=

1 ~

2

,

D[m

x

D[x] или σ~

σ

x

n

mx

n

~

~2

где D[x] ( σx ) – оценка дисперсии случайной величины X.

Оценку дисперсии по выборке (6.2) дает формула

~

1

n

~

2

D[x] =

∑(xk − mx )

.

(6.3)

n −1 k =1

Характеристики суммы и произведения случайных величин. При расчете измерительных приборов на точность прежде всего следует установить связь между детерминированными значениями параметров, после чего можно перейти к вероятностным характеристикам. При этом приходится одновременно учитывать несколько случайных величин, связанных между собой определенной зависимостью. Наиболее распространенными связями между случайными величинами являются их сумма и произведение. Наряду со случайными величинами в расчетах участвуют и неслучайные.

Математическое ожидание неслучайной величины С равно этой величине

M[C] = C .

Дисперсия неслучайной величины С равна нулю

D[C] = 0.

Неслучайную величину можно выносить за знак математического ожидания

M [C x] = C M [x].

65

σ(x) σ( y)

Неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат

D[C x] = C 2 D[x] .

Неслучайную величину можно выносить за знак СКО ее абсолютным значением

σ[C x] = C σ[x].

Математическое ожидание суммы случайных величин равно сумме их математических ожиданий

M[x + y + z +... + q] = M[x] + M[ y] + M[z] +... + M[q].

Математическое ожидание линейной функции случайных величин равно той же линейной функции от математических ожиданий аргументов

M [A x + B y +... + F z + C] = A M [x] + B M [ y] +... + F M [z] + C ,

где A, B, F, C – неслучайные величины.

Если случайные величины независимы в статистическом смысле, т. е. если вероятность появления одной случайной величины не связана с вероятностью появления другой случайной величины, то дисперсия их суммы равна сумме дисперсий каждой из них

D[x + y + z +... + q] = D[x] + D[ y] + D[z] +... + D[q].

Если вероятность появления одной случайной величины, например x, связана с вероятностью появления второй случайной величины, например y, то x и y считаются зависимыми в статистическом смысле. Мерой такой связи является

коэффициент корреляции

kxy = M {[x − M (x)][ y − M ( y)]}.

Если статистической связи нет, то kxy = 0 . Но из некоррелированности случайных величин не всегда следует их независимость. При функциональной связи kxy =1. При наличии статистической связи 0 ≤ kxy ≤1.

Дисперсия суммы двух зависимых случайных величин определяется по формуле

D[x + y] = D[x] + D[ y] + 2kxy σ(x) σ( y) .

При большем числе слагаемых дисперсию суммы находят последовательным сложением.

Вероятностные характеристики произведения независимых случайных величин имеют вид:

n	n
M [∏xi ] = ∏M [xi ];
i=1	i=1

D[x y] = D[x] D[ y] + D[x]M 2 [ y] + M 2 [x] D[ y].

66

Если X1, X2, …, Xn – независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией σ2 , то при

n

неограниченном увеличении n закон распределения суммы ∑X i неограниченно

i=1

приближается к нормальному. Эта теорема называется центральной предельной теоремой для одинаково распределенных слагаемых

6.2. Вероятностные оценки ширины распределения случайных погрешностей

«Предельная» или «максимальная» оценка случайной погрешности. Эта оценка теоретически правомерна только для ограниченных распределений (равномерного, треугольного, трапецеидального и т. п.). Для этих распределений действительно существует такое значение ± X m , которое ограничивает с обеих

сторон возможные значения случайной величины. Однако эти распределения являются лишь теоретической идеализацией и реальные распределения погрешностей, строго говоря, им никогда не соответствуют. Кривые плотности реальных распределений погрешностей, за редкими исключениями, не имеют четко выраженных границ. И поэтому указание для них «предельных» или «максимальных» значений неправомерно. На практике такая оценка есть указание наибольшего по модулю отклонения, встретившегося в данном, произвольно ограниченном ряду наблюдений, так как с увеличением объема выборки экспериментальных данных «предельные» значения монотонно возрастают. «Предельная» погрешность прибора max , найденная экспериментально по 100

отсчетам, всегда будет большей, чем найденная по первым 10 отсчетам.

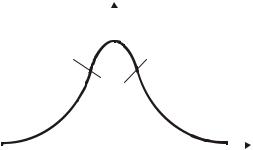
Квантильные оценки случайной погрешности. Площадь, заключенная под кривой плотности распределения (рис. 6.3), согласно правилу нормирования, равна единице, т. е. отражает вероятность всех возможных событий. Эту площадь можно разделить на некоторые части вертикальными линиями. Абсциссы таких

линий называют квантилями. Так, x = x1							на рис. 6.3 есть 25%-ная квантиль, так
			p(x)			как площадь под кривой p(x) слева от нее
						составляет 25% всей площади, а справа –
25%			25%			75%.	Медиана (x = x2		на рис.	6.3) – это
						50%-ная квантиль, так как она делит
						площадь под кривой p(x) на две равные
						части. Между x1 и x3, т. е. 25%- и 75%-ной
25%				25%	x	квантилями,		которые	принято	называть
						сгибами данного распределения, заключено
	x1 x2 x3
						50% всех возможных значений погрешности,
	Рис. 6.3. Квантили					остальные 50% лежат вне этого промежутка.
						На рис. 6.4		x = x3 есть 5%-ная квантиль,

67

так как площадь под кривой p(x) слева от нее составляет 5% всей площади.

Соответственно значения x1, x2, x5, x6, x7 на рис. 6.4 – это 1%-, 2,5%-, 95%-, 97,5%-,

99%-ная квантили. Их принято обозначать соответственно x0,01, x0,025, x0,95, x0,975, x0,99. Интервал значений x между x = x0,05 и x = x0,95 охватывает 90% всех возможных значений случайной величины и называется интерквантильным

промежутком с 90%-ной вероятностью. Его протяженность d0,9 = x0,95 − x0,05 .

Интерквантильный промежуток включает в себя 90% всех возможных значений случайной величины и т. д.

	p(x)
		98%
		95%
		90%
5%		5%
x1 x2 x3	x4	x
		x5 x6 x7
Рис. 6.4. Интерквантильные промежутки

На основании такого подхода вводится понятие квантильных оценок погрешности, т. е. значений погрешности с заданной доверительной вероятностью Pд, как границ интервала неопределенности ± д = ±dд2 , на

протяжении которого встречается Pд процентов всех значений погрешности, а 1− Pд процентов общего числа их значений остаются за границами этого

интервала.

Таким образом, доверительное значение случайной погрешности есть ее

максимальное значение с указанной доверительной вероятностью Pд, т. е. сообщение, что часть реализаций погрешности с вероятностью 1− Pд = q может

быть больше указанного значения погрешности.

Обозначение доверительной погрешности снабжают индексом, численно равным принятой доверительной вероятности, например 0,9 при Pд = 0,9 ; 0,95

при Pд = 0,95 и т. д.

Исторически сложилось так, что в разных областях знаний используют различные значения доверительной вероятности, равные 0,5; 0,8; 0,9; 0,95; 0,99. Так в области расчета артиллерийской стрельбы общепринятой является срединная ошибка, т. е. погрешность с доверительной вероятностью Pд = 0,5,

когда 50% всех возможных отклонений меньше ее, а другие 50% – больше. Доверительная вероятность Pд = 0,8 является общепринятой в теории и практике

оценки надежности средств автоматики, электронной и измерительной техники.

68

Погрешность 0,9 обладает тем уникальным свойством, что для широкого

класса законов распределения вероятностей только она имеет соотношение со средним квадратическим отклонением в виде

0,9 =1,6σ

независимо от вида закона распределения. Поэтому ГОСТ 11.001–73 при отсутствии данных о виде закона распределения для определения двусторонней доверительной вероятности предписывал использовать только Pд = 0,9 .

При наличии у прибора кроме чисто случайной составляющей еще и систематической погрешности θ выход возможных значений погрешности за границы доверительного интервала ± (θ+ 0,9 ) становится практически

односторонним. Для односторонней вероятности выхода за пределы интервала

±д при отсутствии данных о виде закона распределения ГОСТ 11.001–73

предписывал использование доверительной вероятности Pд = 0,95 . Доверительная вероятность Pд = 0,99 используется лишь при указании погрешностей первичных и рабочих эталонов.

Достоверность определения доверительного значения погрешности по экспериментальным данным. Достоинство доверительного значения погрешности состоит в том, что оно может быть достаточно просто оценено прямо по экспериментальным данным.

Пусть проведена серия из n измерений. Из наблюдавшихся n случайных погрешностей составляют вариационный ряд, располагая их в порядке возрастания:

(1) ≤ (2) ≤ (3) ≤ ... ≤ (n) .

Далее используется предположение, что каждый из членов вариационного ряда является оценкой соответствующих квантилей, которые делят весь интервал возможных вероятностей (от 0 до 1) на n + 1 частей с равными значениями вероятности, иными словами, вероятности попадания значений погрешности в каждый из интервалов

(−	∞; (1) ); (	(1) ; (2) ); ...;	(	(n−1) ; (n) ); (		(n) ; + ∞)
предполагаются	одинаковыми, а следовательно,				равными 1 (n +1) .		Отсюда
каждое из наблюдавшихся		значений	(i)	может	быть	принято как	оценка

i(n +1) ·100%-ной квантили.

Таким образом, практическое определение д сводится к тому, что из всех

полученных отсчетов отбрасываются наиболее удаленные от центра, а следовательно, самые ненадежные отсчеты. Если при переменном n отбрасывается постоянная относительная доля всех отсчетов, то определяемое по крайним членам оставшегося вариационного ряда значение д , в отличие от

«предельной» погрешности прибора max , с ростом длины n серии отсчетов не

69

возрастает, а стабилизируется и оказывается тем более устойчивым, чем больше объем выборки n.

При этом необходимо учитывать, что по ограниченным экспериментальным данным мы получаем не точные доверительные значения, а лишь их приближенные значения – оценки. Достоверность квантильных оценок повышается с понижением значений Pд, а при постоянном Pд – с ростом числа

отсчетов n. Поэтому квантильные оценки с большими доверительными вероятностями могут быть найдены только при большом числе отсчетов. Действительно, так как вариационный ряд из n членов определяет границы n + 1 интервалов, вероятность попадания в которые принимается одинаковой, то при

отбрасывании лишь интервалов (−∞; (1) ) и (	(n); + ∞) оценка	погрешности
может быть определена с доверительной вероятностью не большей, чем
Pд ≤ (n −1) (n +1) .
При небольших объемах выборки n достоверность оценки		д , найденной
таким путем, очень мала. Для определения оценки	д с большей достоверностью

с каждого из концов вариационного ряда должны быть отброшены не только пустые интервалы (−∞; (1) ) и ( (n) ; + ∞), но и какое-то число фактических

отсчетов. Располагая рядом из n отсчетов и отбрасывая с каждого из концов ряда

по nотб отсчетов, можно определить д с	доверительной вероятностью не
большей, чем
Pд ≤ (n −1−2nотб)	(n +1) .

Отсюда число отсчетов n, необходимое для определения по экспериментальным данным д с заданной вероятностью Pд, будет не меньшим, чем

n≥ (1+ Pд +2nотб)(1− Pд)≈ [2(1+nотб)](1− Pд).

идля различных значений Pд и nотб = 1 приведено в табл. 6.1.

									Таблица 6.1
	Pд	0,8	0,9		0,95	0,98		0,99	0,995	0,997
	n	20	40		80	200		400	800	1333
	Основным недостатком доверительного значения погрешности									д при
произвольно выбираемых				Pд, как и «предельной»				погрешности max ,		является

невозможность их суммирования, так как доверительный интервал суммы не равен сумме доверительных интервалов слагаемых.

Пример 6.1. Определить доверительный интервал, в который с вероятностью Pд попадают значения погрешности при условии, что: а) распределение значений

погрешности равномерное; б) значения погрешности распределены по треугольному закону (закону Симпсона).

70