OTIP

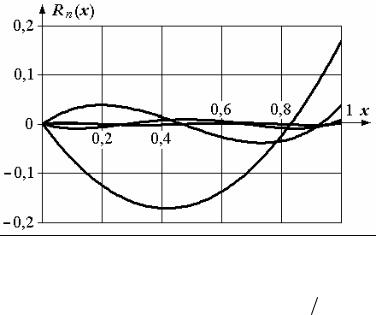
Так, например, пусть x изменяется в пределах от a = – 0,4 до b = 0,4. Перейдем к переменной t, изменяющейся от – 1 до + 1:

t = (2x −(−0,4) −0,4)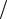[0,4 −(−0,4)]= 2x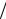0,8 = x0,4 .

Таблица 9.2

Характеристики полиномов Чебышева Rn (x)

				Точки наибольшего	Значе-
					ния наи-
n		Rn (x)	Корни xk	отклонения	большего
				xi*	откло-
					нения λk
2		x2 −0,8284x	0; 0,8284	0,4142	0,1716
3	x3 −1,3923x2 +0,4308x		0; 0,4641; 0,9282	0,1961; 0,7320; 1	0,0385
4	x4	−1,9209x3 +1,1135x2 −	0; 0,2813; 0,6761;	0,1127; 0,4802;	0,0091
		−0,1835x	0,9604	0,8478; 1
5	x5	−2,4373x4 + 2,0477x3 −	0; 0,1862; 0,4875;	0,0728; 0,3291;	0,0022
		−0,6781x2 +0,0698x	0,7887; 0,9749	0,6458; 0,9021

Рис. 9.12. Функции Rn (x) в пределах [0; 1]

Для полинома Rn (x) замена переменных осуществляется по формуле

t = x b .	(9.74)
Так, например, для области определения	x [0; 0,4] замена переменной

производится по формуле t = x0,4 .

Применение полиномов того или иного вида при точностном синтезе обусловлено их спецификой. Полиномы Pn (x) определены в области входных

воздействий [– 1; + 1], поэтому их применение наиболее целесообразно при синтезе средств, реализующих относительные измерения. При этом полиномы

141

нечетных степеней (n = 3; 5; …) имеют нулевые корни, а полиномы четных степеней (n = 2; 4; …) в середине диапазона имеют наибольшее отклонение. Полиномы Rn (x) независимо от степени имеют нулевые корни, однако

определены в области [0; + 1]. Для объектов с симметричным диапазоном

измерения наряду с полиномами Pn (x) применяются полиномы Qn (x)						(табл. 9.3,
рис. 9.13), которые определены на интервале				[– 1; + 1], однако для четных
степеней имеют нулевые корни.
					Таблица 9.3
		Характеристики полиномов Чебышева Qn (x)
					Точки наибольшего	Значе-
						ния наи-
	n	Qn (x)	Корни xk		отклонения	большего
					xi*	откло-
						нения λk
	4	x4 −0,8284x2	0; ± 0,9102		± 1; ± 0,6436	0,1716
	6	x6 −1,3923x4 +0,4308x2	0; ± 0,6813;		± 1; ± 0,8556;	0,0385
			± 0,9634		± 0,4429

Рис. 9.13. Функции Qn (x) в пределах [– 1; 1]

Алгоритм синтеза. При синтезе параметров измерительных приборов по критерию минимума погрешности приближения необходимо выполнить следующие операции.

1.Составить математическое описание объекта проектирования и получить аналитическое выражение для погрешности схемы.

2.Определить допускаемое значение погрешности приближения.

Допускаемое значение yсх выбирается с учетом назначения измерительного

прибора и требуемой его точности. Следует помнить, что погрешность приближения является лишь составляющей полной погрешности y, поэтому

142

следует обеспечить запас по точности на другие составляющие. Рекомендуется соотношение

yсх		≈ 0,1		y		,	(9.75)

где y – допускаемое значение полной погрешности.

3. Выбрать вид полинома Чебышева.

Выбор вида полинома осуществляется на основе анализа вида расчетной характеристики, диапазона изменения входного воздействия, характеристики отсчетного устройства и т. п. Если прибор предназначен для относительных измерений при симметричных пределах и расположении нуля в середине диапазона, то для точностного синтеза рекомендуются полиномы Pn (x) с

нечетными степенями или Qn (x) со степенями n = 4; 6. Если ноль находится в начале шкалы, то предпочтительными являются полиномы Rn (x) .

4. Определить наименьшую степень полинома.

Степень полинома должна обеспечивать идентичность вида функции погрешности в рассматриваемом диапазоне виду полинома Чебышева, поэтому целесообразно вначале определиться с видом функции погрешности. Следует проанализировать функцию погрешности, построить ее график в исследуемом диапазоне, сравнить этот график с графиками полиномов Чебышева, определиться с ожидаемым количеством корней этой функции в диапазоне.

На практике на первом этапе синтеза рекомендуется выбирать n = 2 или n = 3, а затем уточнять его. Увеличение n приводит в общем случае к повышению точности расчета, а значит, к увеличению точности измерительного прибора. Однако чрезмерное повышение n приводит к существенному росту сложности расчетов. Поэтому необходимо брать наименьшее значение степени n, обеспечивающее предельную погрешность приближения.

5. Выполнить замену переменной.

Замену переменных проводят в соответствии с выражениями (9.73) для полиномов Pn (x) и Qn (x) или (9.74) для полиномов Rn (x) .

6. Определить оптимальные значения параметров.

Этот этап является основным. Необходимо определить значения внутренних параметров объекта, обеспечивающие идентичность функции погрешности выбранному полиному Чебышева. Данная задача решается приближенными методами, при этом в зависимости от требуемой точности и сложности объекта можно воспользоваться разными подходами.

• Первый подход основывается на положении о том, что два многочлена степени n считаются равными, если равны их коэффициенты при аргументах в соответствующих степенях. Алгоритм реализации этого подхода:

– аналитическое выражение для погрешности приближения разложить в ряд по степеням аргумента;

143

–приравнять числовые коэффициенты полиномов Чебышева (табличные данные) коэффициентам ряда (с буквенными обозначениями параметров) при

xв соответствующих степенях, получить систему n уравнений;

–решить полученную систему n уравнений относительно неизвестных {q1, q2 , ..., qN }. Максимальное число неизвестных параметров

qs , s =1, N , которые можно найти, решая систему уравнений, равно степени

полинома n. Число параметров N может отличаться от n. Если N < n, то учитывают не все коэффициенты, а лишь N коэффициентов при больших степенях аргумента. Если N > n, то ряд параметров qs выбирают из

конструктивных соображений, оставляя в качестве неизвестных не более n параметров.

Этот подход является наиболее достоверным, но и более трудоемким.

• В основу второго подхода положено предположение о том, что два многочлена степени n считаются равными, если равны их корни. Алгоритм реализации этого подхода:

–из таблиц для выбранного типа полинома с учетом n определить корни полинома Чебышева;

–подставить значения корней в функцию погрешности и приравнять ее к нулю, получить систему n уравнений с неизвестными (число уравнений может быть меньше n, если требуется определить меньшее количество неизвестных параметров qs );

–решить полученную систему относительно неизвестных параметров qs .

Второй подход является более простым, хотя и менее точным.

• Наиболее простой третий подход позволяет получить удовлетворительные результаты для сравнительно простых измерительных приборов с нелинейными характеристиками. В основу положено разложение функции погрешности в ряд (как и в первом варианте) и приравнивание нулю коэффициентов при аргументах в степени, большей 1. Алгоритм реализации:

–аналитическое выражение для погрешности приближения разложить в ряд по степеням аргумента;

–коэффициенты при аргументах в степенях, больших 1, приравнять 0 и получить систему N уравнений;

–решить систему относительно N неизвестных параметров qs , s =1, N .

7.Определить максимальное значение погрешности приближения, проверить эффективность синтеза.

Максимальное значение погрешности yсх max определяют из полученного аналитического выражения для yсх и найденных оптимальных значений параметров путем вычисления значения погрешности в точках, соответствующих точкам наибольшего отклонения полиномов xi* (см. табл. 9.1, 9.2, 9.3).

Следует отметить, что представление функции погрешности в виде полинома Чебышева является приближенным. Поэтому для более точного определения

144

максимального значения погрешности приближения следует, исследовав полученную функцию погрешности на экстремум, уточнить значения xi* . Можно

также определить максимальное значение погрешности, построив ее функцию на всем диапазоне преобразования с заданным шагом аргумента.

Точностный					синтез считается законченным при выполнении условия
yсх max ≤		yсх		.	Если условие не выполняется, то выбирают следующее более

высокое значение степени полинома Чебышева и проводят уточняющий расчет.

Примеры синтеза

Пример 9.1. Синусный рычажно-зубчатый преобразователь.

Определить оптимальное значение длины рычага q прибора (см. рис. 5.3) при следующих исходных данных: граничные значения диапазона измерений a = – 0,4 мм; b = 0,4 мм; цена деления шкалы c = 0,01 мм; число делений шкалы Zшк = 80; угол шкалы Θшк = 2π3.

1. Пользуясь выражением для расчетной характеристики прибора (5.14) и учитывая, что заданная характеристика имеет вид: y0 = x , запишем

аналитическое выражение для погрешности приближения

yсх = yр − y0 =	Zшк c		z1	arcsin	x	− x .
			z2		q
	Θшк

2. Допускаемое значение погрешности приближения определим согласно

(9.75)

yсх ≈ 0,1 y = 0,1c = 0,001 мм.

3.Анализируя схему прибора и принимая во внимание симметричность диапазона измерений, воспользуемся для синтеза полиномом Чебышева Pn (x) .

4.Степень полинома примем равной n = 3, P3(x) = x3 −0,75x .

5.Заменим переменную согласно формуле (9.73)

t= (2x − a − b)(b − a)= (2x + 0,4 −0,4)[0,4 + 0,4]= x0,4 .

6.Определим оптимальные значения параметров.

Из конструктивных соображений примем отношение чисел зубцов соответствующих шестерен z1 z2 =10 и найдем оптимальное значение длины

рычага q. Воспользуемся вторым из рассмотренных подходов, в котором используются значения корней полиномов.

Из табл. 9.1 определим корень полинома третьей степени (неизвестный параметр один, поэтому необходим только один корень). Их трех корней 0 не может применяться, поскольку полином P3(x) при нулевом аргументе независимо

от q всегда обращается в нуль. Воспользуемся значением xk = 0,8660. Подставим корень в функцию погрешности и приравняем ее к нулю

yсх =	80 0,01 3	0,4 0,866			−0,4 0,866	= 0.
	2π	10 arcsin	q

145

Решая полученное уравнение относительно q, найдем оптимальное значение qопт1:

0,4 0,866			=	0,4 0,866 2π	= 0,09069	;
arcsin	q			80 0,01 3 10

qопт1 = 3,8248 мм.

7. Определим максимальное значение погрешности при найденном qопт1, выберем xi* =1

	yсх max =	80 0,01 3		0,4 1		−0,4 1 = 0,20 10−3
		2π	10 arcsin				мм.
				3,8248

Поскольку yсх max < yсх , расчет можно считать завершенным.

Аналогичные расчеты, выполненные для полинома второй степени, дают результат qопт2 = 3,8232 мм, при этом максимальное значение погрешности 0,37·10–3 мм, что также является вполне удовлетворительным результатом.

Пример 9.2. Электрический термометр.

При построении термисторного термометра согласно схеме, представленной на рис. 9.14, необходимо определить параметры измерительной цепи, обеспечивающие минимальную погрешность приближения при работе прибора в

диапазоне T [20; 70] oC.

	R1						R2
		Rд		PA
							U
	RТ						R3

Рис. 9.14. Схема электрического термометра

Из анализа априорной информации и принципиальной схемы прибора устанавливаем, что он включает в себя три последовательно соединенные преобразователя: полупроводниковый термометр сопротивления (термистор), преобразующий температуру T в сопротивление RТ; неуравновешенный измерительный мост, преобразующий RТ в силу тока I в измерительной диагонали; микроамперметр PA, отградуированный в единицах температуры и имеющий равномерную шкалу. Заданная характеристика является линейной:

I0 = k(T −Tн ).

(9.76)

где Tн – нижний предел измерения; k =1 мкА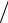 оС – масштабный коэффициент.

1. Согласно приведенному выше алгоритму определим расчетную характеристику прибора и аналитическое выражение для погрешности приближения. Для этого запишем характеристики преобразователей.

Для термистора по справочным данным имеем

146

RT = R0 exp(B T ),

(9.77)

где R0 и В – внутренние параметры преобразователя.

Характеристика термистора, таким образом, существенно нелинейная. Ее график для выбранных в качестве примера параметров (В = 80; R0 = 790 Ом)

представлен на рис. 9.15.

Рис. 9.15. Статическая характеристика термистора

Для мостовой схемы (см. рис. 9.14) функция преобразования имеет вид

I =U				RT R2 − R1R3			.	(9.78)
	R	(R	+ R )(R + R )+ R R (R + R )+ R R (R			+ R )
		д T	1 2 3	T 1 2 3	2 3 T	1

Видно, что характеристика моста также существенно нелинейная. Следовательно, расчетная характеристика прибора, получаемая путем

подстановки (9.77) в (9.78), является нелинейной, а заданная характеристика – линейная, т. е. имеет место погрешность приближения.

С учетом (9.75) и (9.78) получим выражение для погрешности

	Iсх =U		RT R2 − R1R3					−k(T −Tн ),
		Rд(RT	+ R1 )(R2 + R3 )+ RT R1(R2			+ R3 )+ R2R3(RT + R1 )
2.	Принимая во внимание, что ноль находится в начале шкалы, воспользуемся
для синтеза полиномом Чебышева Rn (x) .
3.	Примем n = 3,		R (x) = x3 −1,3923x2 + 0,4308x . Корни: xk1 = 0; xk2 = 0,4641;
xk3 = 0,9282.			3
4.	Для перехода от диапазона [Tн; Tв] к диапазону [0; 1] выполним замену
переменной согласно формуле
			x =	T		−T ,
				Tв −Tн		н

следовательно,

T = x (Tв −Tн )+Tн .

Отсюда с учетом исходных данных (Tн = 20 oC; Tв = 70 oC) получим значения переменной T, соответствующие корням xk1, xk2, xk3 полинома Чебышева R3(x) :

147

T1 = Tн = 20o C ;

T2 = 0,4641(Tв −Tн )+Tн = 43,205o C ;

T3 = 0,9282(Tв −Tн )+Tн = 66,41o C .

Значениям		T1,	T2, T3		соответствуют значения сопротивлений
R	= 4,318 104	Ом;	R	= 5,038 103	Ом; R	= 2,638 103 Ом.
T1			T 2		T 3

5. Составим систему трех уравнений, подставляя найденные значения RT i в выражение для погрешности приближения и приравнивая его нулю:

	U					RT1R2 − R1R3				= k(T1 −Tн );
				Rд(RT1	+ R1 )(R2	+ R3 )+ RT1R1(R2 + R3 )+ R2R3(RT1	+ R1 )
	U					RT 2R2 − R1R3				= k(T2 −Tн );
		Rд(RT 2			+ R1 )(R2	+ R3 )+ RT 2R1(R2 + R3 )+ R2R3(RT 2	+ R1 )
	U					RT 3R2 − R1R3				= k(T3 −Tн ).
			Rд(RT 3		+ R1 )(R2	+ R3 )+ RT 3R1(R2 + R3 )+ R2R3(RT 3	+ R1 )

6. Определим значения параметров. Решением полученной системы можно найти только три неизвестных параметра. Из конструктивных соображений принимаем R1 = R2 , сопротивление в диагонали моста с учетом добавочного

резистора и характеристик микроамперметра Rд =1000 Ом.

Из первого уравнения системы получим R3 = RT1 .

Решением системы оставшихся двух уравнений определим неизвестные параметры R1, R2, U: R1 = R2 = 91,44 Ом; U = −1,74 В.

7. Определим функцию погрешности приближения. Расчетная зависимость Iсх (T ) имеет вид, представленный на рис. 9.16. Анализ полученной кривой

показывает, что с учетом знака она соответствует графику полинома Чебышева R3(x) третьей степени (см. рис. 9.12). При этом максимальные значения

погрешности соответствуют координатам точек наибольшего отклонения xi* полинома и не превышают 1,4 мкА.

Рис. 9.16. Зависимость погрешности от температуры

148

Таким образом, даже при такой сложной характеристике прибора при существенной нелинейности используемых преобразователей рассматриваемый метод синтеза параметров весьма эффективен.

9.8. Синтез приборов по критерию минимума математического ожидания погрешности

Математическое ожидание суммарной погрешности представляет собой систематическую составляющую погрешности. При выполнении определенных условий данная составляющая может быть существенно уменьшена, сведена к минимуму, а в ряде случаев и полностью скомпенсирована.

Пусть измерительный прибор имеет погрешность вида

Y = F ( X ,q) − Fo ( X ) ,

(9.79)

где F(X ,q) – функция преобразования реального прибора (реальная характеристика прибора); Fo ( X ) – функция преобразования идеального прибора (требуемая характеристика); q = {q1, q2 , ..., qn } – параметры реального прибора.

Пусть известно, что входной сигнал X изменяется в интервале		X [ Xo , X* ] .
Введем интегральный критерий точности системы
X	*
Φ = ∫	M [ Y ]2 dX .	(9.80)

X o

где Ф – интеграл функции математического ожидания погрешности прибора в диапазоне измерения прибора [ Xo , X* ] .

Задача заключается в определении параметров q1, q2 , ..., qn прибора,

доставляющих минимум критерию (9.80).

Исследуя функцию (9.80) на экстремум, получим необходимые и достаточные условия минимума критерия Ф по переменным q1, q2 , ..., qn

∂Φ	= 0 ,	i =		.	(9.81)
			1, n
∂q
i
Решив систему уравнений (9.81),		найдем значения искомых			параметров
q ={q1, q2 , ..., qn }.

Пример 9.3. В качестве исходной информации заданы: F( X , a, b) = a + bX 2 – квадратичная функция преобразования прибора; F0 ( X ) = kX – требуемая линейная характеристика; [0, X* ] – диапазон измерения прибора.

Определить значения параметров a и b из условия минимума математического

X *

ожидания погрешности Φ = ∫ M [F − F0 ]2 dX .

0

Для решения поставленной задачи составим явное выражение для критерия

149

Φ = X∫* (a +bX 2 −kX )2dX = a2 X* −akX*2 + 1 (2ab −2bk + k2 )X*3 +																				1 b2 X*2 .	(9.82)
0													3							5
Использовав (9.82), составим уравнения (9.81) для определения параметров:
	∂Φ		= 0					~ 2aX			* −kX*2			+		2b	X*3 = 0;
		∂a
																3
		∂Φ		= 0 ~ 2 (a −k )X*3										+		2 bX*2 = 0
		∂b						3								5
или
									2		3				2
		(2X* )a +							3	X*		b = kX* ;
																					(9.83)
			2				3		2			2		2				3
					X						X					kX			.
						*		a +				*	b =					*
			3						5					3

Решив систему уравнений (9.83), относительно a, b, получим такие их значения, которые доставляют минимум критерию. Например, при k = 1, X* =1, получим:

F = 1 +	15 X 2 ; F = X .
2	8	0

Рассмотренная задача синтеза прибора относится к задачам метода наименьших квадратов.

9.9. Синтез приборов по критерию минимума дисперсии случайной погрешности

Случайная погрешность является наиболее неблагоприятной составляющей погрешности, поскольку ее гораздо сложнее компенсировать.

Математическая формулировка задачи минимизации случайной погрешности состоит в следующем: пусть задана общая требуемая чувствительность прибора S*, необходимо так распределить чувствительность между отдельными элементами, случайная погрешность каждого из которых характеризуется

дисперсией Di (i =1, n , n – количество элементов прибора), чтобы общая

погрешность имела минимально возможное значение.

Для решения поставленной задачи необходимо выполнить следующие действия:

1) ввести условие равенства общей чувствительности заданному значению

ϕ = S* − f (S , ..., S	n	) ;	(9.84)
1

2) записать выражение для дисперсии суммы независимых случайных погрешностей отдельных звеньев

n	(9.85)
D = ∑β2D ,
i i
i=1

150