OTIP

Формальным определением энтропийного значения случайной величины являются соотношения

H (x xи ) = ln d и d = 2 э,

отсюда

d = exp[H (xxи )] и э = 0,5exp[H (x xи )] .

Соотношение между энтропийным и средним квадратическим значениями погрешности. Для разных законов распределения соотношение между энтропийным и средним квадратическим значениями погрешности различно. Это соотношение характеризуется значением энтропийного коэффициента данного закона распределения

k = σэ .

• Для равномерного распределения: э = 3 σ ≈1,73σ и k =1,73.

• Для нормального распределения: э = σ 2πe 2 ≈ 2,066 σ и k = 2,066.

•Для треугольного распределения Симпсона: k = 6e 2 ≈ 2,02 .

•Для распределения Лапласа: k =1,93.

•Для арксинусаидального распределения: k = π 8 ≈1,11.

Максимально возможное значение энтропийного коэффициента k = 2,066 имеет нормальное распределение. Поэтому для наиболее часто встречающихся на практике распределений энтропийное значение погрешности колеблется от э =1,11σ у арксинусоидального распределения до э = 2,066 σ у нормального

распределения и при известном законе распределения может быть найдено как

э = k σ.

Соотношение между энтропийным и доверительным значениями погрешностей. Как видно из рис. 6.9, энтропийный интервал неопределенности d = 2 э охватывает лишь ту часть распределения, в которой сосредоточена

основная часть возможных значений случайной погрешности, в то время как некоторая их доля остается за границами этого интервала. Поэтому для любого распределения может быть указано такое значение доверительной вероятности Pд, при котором энтропийное и доверительное значения погрешности совпадают.

7.РАСЧЕТ ДИНАМИЧЕСКИХ ПОГРЕШНОСТЕЙ

7.1.Общие понятия и подходы к расчету

Динамические погрешности возникают вследствие фазовых запаздываний сигналов в элементах прибора и в результате влияния на приборы вредных переменных возмущений. Погрешности, вызванные фазовыми запаздываниями сигналов в элементах приборов, называются собственными динамическими

81

погрешностями, а погрешности, обусловленные вредными возмущениями, –

вынужденными динамическими погрешностями или помехами.

Динамические погрешности присущи всем приборам, работающим в динамическом режиме измерения. Вынужденные динамические погрешности особенно значительны в приборах, работающих на подвижном основании.

Подходы к расчету рассматриваемых погрешностей во многом зависят от причины их возникновения и структуры динамической системы, заложенной в основу работы прибора. Динамические системы классифицируются на две группы: линейные и нелинейные. Линейными называют динамические системы, содержащие только линейные элементы. Если в измерительном приборе хотя бы одно звено является нелинейным, то такой прибор относят к нелинейным динамическим системам.

Нелинейные измерительные приборы описываются нелинейными дифференциальными уравнениями, включающими параметры звеньев, которые зависят от входной величины и от значения помехи. Все многообразие нелинейных систем может быть разделено на две группы:

–приборы с существенно нелинейными характеристиками (к этому классу относят приборы, содержащие элементы, характеристики которых не могут быть линеаризованы в требуемом диапазоне без потери их существенных особенностей);

–приборы с несущественно нелинейными характеристиками (приборы содержат звенья, характеристики которых могут быть линеаризованы в достаточно широком диапазоне без потери их существенных особенностей).

Анализ существенно нелинейных приборов является весьма трудоемкой задачей. При анализе объектов с несущественно нелинейными характеристиками прежде всего линеаризуют характеристику, а затем прибор рассматривают как линейную систему.

Собственные динамические погрешности подразделяются на четыре типа:

•Погрешности формы, которые характеризуют степень искажения формы выходного сигнала y(t) по сравнению с входным сигналом x(t)

y(t) = y(t) − x(t) .

(7.1)

• Операционные погрешности, которые характеризуют степень искажения передаточной функции по отношению к статическому режиму

W ( p) =W ( p) −W (0) .

(7.2)

• Частотные погрешности, из которых могут быть получены амплитудные и фазовые частотные погрешности, т.е. искажения амплитуды и фазы в зависимости от частоты входного сигнала

H (ω) = H (ω) − H (0).	(7.3)
• Погрешности переходного процесса
h(t) = h(t) − h(∞) .	(7.4)

82

Правые части выражений (7.1)–(7.4) представляют собой разности между соответствующими характеристиками реального и идеального приборов. Видно, что динамические погрешности тем меньше, чем больше характеристики реального прибора приближаются к характеристикам идеального прибора. Если известно одно из рассмотренных уравнений, то можно получить любое другое.

Например, если известны операционные погрешности			W ( p) , то частотные
погрешности получаются из соотношения W ( p)		p= jω =	H (ω) , а погрешности

y(t) , h(t) получаются путем применения обратных преобразований Лапласа или Фурье к W ( p) или H(ω) соответственно.

Расчет погрешностей в каждом конкретном случае требует индивидуального подхода, хотя выделяются группы задач, при решении которых можно воспользоваться определенными рекомендациями. Рассмотрим некоторые из таких подходов.

7.2. Определение динамических погрешностей при детерминированных входных воздействиях

На практике чисто детерминированных воздействий не бывает. Однако при использовании измерительных приборов среди ансамбля возможных входных сигналов, для преобразования которых они предназначены, часто имеют место типовые входные воздействия, которые достаточно точно описываются детерминированными функциями времени. В некоторых случаях необходимо определить погрешность при наименее благоприятном из возможных входных воздействий. Тогда возникает проблема в оценке погрешности прибора при известном входном воздействии.

Динамическая точность в данном случае может характеризоваться абсолютной величиной разности расчетной и реальной выходных величин.

Пусть x(t) – известное входное воздействие на линейную динамическую систему со значением чувствительности – S. Тогда при отсутствии динамической погрешности расчетное значение выходного сигнала имеет вид

yр(t) = x(t) S .

Ввиду неидеальности измерительной системы прибора будет иметь место динамическая погрешность yдин(t), определяемая выражением

yдин(t) = yр(t) − y(t) ,

где y(t) – действительное значение выходного сигнала.

Согласно динамическим характеристикам выходной сигнал может быть определен с помощью интеграла свертки

∞

y(t) = ∫ x(t − τ) h(τ)dτ,

0

83

где h(τ) – весовая функция или импульсная переходная характеристика данного прибора.

Тогда динамическую погрешность можно представить в виде

∞
yдин(t) = S x(t) − ∫ x(t − τ) h(τ)dτ.	(7.5)
0

Таким образом, расчет динамической погрешности сводится к решению интеграла свертки. Рассмотрим подход к решению.

Входной сигнал x(t) представим в виде многочлена степени r, тогда x(t − τ) можно разложить в ряд Тейлора

&&

x

(r)

(t)

&

x(t)

τ

2

+... + (

−1)

r

τ

r

.

(7.6)

2!

r!

x(t − τ) = x(t) − x(t) τ +

Разложение имеет конечное

число

членов,

поскольку x(t)

– полином

степени r. Подставив значение x(t − τ) из (7.6) в (7.5), после упрощений получим

∞

&

∞

+ x

(r)

(t)

(−1)r+1 ∞

r

h(τ)dτ.(7.7)

yдин(t) = S x(t) − x(t) ∫h(τ)dτ + x(t)

∫τ h(τ)dτ +...

r!

∫τ

0

0

0

Введем обозначения:

∞

С0 = S − ∫h(τ)dτ;

∞

0

τ h(τ)dτ;

С1 = ∫

(7.8)

0

...

r+1 ∞

Сr = (−1)

r

∫τ

h(τ)dτ.

0

Запишем (7.7) с учетом (7.8)

yдин(t) = С0 x(t) + С1

x(t) +... +

Сr

x

(r)

(t) .

(7.9)

&

r!

Анализ (7.9) показывает, что для снижения динамических погрешностей необходимо уменьшать, а по возможности обеспечить равенство нулю первых членов данного выражения. Этого можно добиться двумя путями: уменьшением

сомножителей типа x(r) (t) и уменьшением коэффициентов Ci. Сомножители

x(r) (t) определяются видом входного сигнала, а коэффициенты Ci – характеристиками измерительного прибора.

Коэффициенты C0, C1, C2, …, Cr – носят название коэффициентов ошибок. Они могут быть легко вычислены с помощью передаточной функции

Ci =	d i [S −W	( p)]	.	(7.10)
	(dp)i
			p=0

84

Коэффициенты ошибок имеют определенный физический смысл. Они характеризуют порядок астатизма измерительного прибора. Так, например, если C0 = C1 = 0, то говорят, что прибор характеризуется астатизмом второго порядка, то есть любое входное воздействие, имеющее линейную функцию времени, будет отрабатываться без динамической погрешности.

Полученный вывод дает предпосылки для анализа и синтеза измерительного прибора в динамическом режиме. Составив математическое описание W ( p) , по

формуле (7.10) можно рассчитать коэффициенты ошибок Ci и по характеристике входного воздействия x(t) определить ожидаемую динамическую погрешность.

При синтезе решают задачу оптимизации выбора параметров измерительного прибора, при которых заданное входное воздействие x(t) будет преобразовываться без динамической погрешности или эта погрешность будет иметь минимально возможное значение.

Например, если входное воздействие изменяется согласно выражению x(t) = a + bt + d t2 , то условия астатизма третьего порядка, при которых данный сигнал будет отрабатываться без динамической погрешности имеют вид:

C0 = 0, C1 = 0, C2 = 0.

После записи выражений для коэффициентов ошибок Ci из (7.10) и решения полученной системы уравнений относительно внутренних параметров измерительного прибора, определяются оптимальные значения параметров, обеспечивающие астатизм третьего порядка.

Если задача исключения динамических погрешностей не имеет решения, можно решить задачу их минимизации, исследовав выражение для динамической погрешности на экстремум:

y	дин	(t) = С	0	(a + bt + d t2 ) + С (b + 2d t) + С1		2d .
				1	2!
Рассмотрим операционную динамическую погрешность						W ( p) . Преобразуем

выражение (7.2) для операционной погрешности, разложив в ряд Тейлора передаточную функцию W ( p) и подставив результат разложения в формулу (7.2). Тогда получим

			∞	p	i
			W ( p) = ∑W (i) (0)			,	(7.11)
				i!
			i=0
где W (i) (0)	= d iW ( p)		– коэффициенты ошибок операционных погрешностей.
	(dp)i		p=0

Можно отметить связь между коэффициентами Ci и W (i) (0) в выражениях

(7.9) и (7.11):

C0 =1 −W (0) ; C1 =W I (0) ; C2 =W II (0) , …, Cr =W (r) (0) .

Если в выражении (7.11) положить несколько первых членов равными нулю:

85

W I (0) = 0, W II (0) = 0, ... , W (r) (0) = 0 ,

(7.12)

то можно уменьшить динамические погрешности прибора. Очевидно, число уравнений (7.12) не может превышать числа независимых параметров, входящих в передаточную функцию W ( p) .

Пример 7.1. Дана передаточная функция прибора

	S ω2
W ( p) =	o		.	(7.13)
	p2 + 2d ω	p + ω2
	o	o

Перейдем к новой переменной q = pωo и приведем выражение (7.13) к виду

S
W (q) = q2 + 2d q +1 .	(7.14)

В этом выражении только один независимый параметр d, поэтому из системы (7.12) можно взять только одно уравнение.

Определим такое значение параметра d, при котором погрешности прибора минимальны. Для этого найдем производные функции (7.14) и поочередно будем

приравнивать их нулю. Заметим, что уравнение W I (0) = 0 дает физически нереализуемую систему. Если W II (0) = 0 , то d = 0,5. Аналогично из W III (0) = 0

находим d = 0,707; W IV (0) = 0 d = 0,812; W V (0) = 0 d = 0,867	и т. д.
Отсюда следует, что чем более высокая производная	W ( p) при p → 0
приравнивается нулю, тем больше система приближается	к апериодической
(d = 1).

Оптимальные значения коэффициента относительного затухания с точки зрения минимума операционных погрешностей являются d = 0,7–0,8. По критерию минимума yдин(t) получаются несколько меньшие значения d.

Динамические погрешности приборов можно рассматривать в частотной области. Для этой цели от комплексной частотной погрешности H(ω) переходят к амплитудно- и фазочастотной погрешностям

A(ω) = A(ω) − A(0);		(7.15)
ϕ(ω) = ϕ(ω) − ϕ(0),

где A(ω) = H (ω)2 = H 2 (ω).

Разлагая A(ω) в ряд по ω и подставляя в первое уравнение (7.15), получим

		∞	i	,
		A(ω) = ∑A(i) (0)	ω
		i=0	i!
где A(i) (0) = d i A(ω)		– коэффициенты ошибок в частотной области, связанные
(dω)i		ω=0
с коэффициентами Ci и W (i) (0) .

86

7.3. Расчет динамической погрешности, вызванной несоответствием параметров номинальным значениям

Несоответствие параметров номинальным значениям, возникающее при изготовлении или эксплуатации измерительного прибора, приводит к появлению не только статической, но и динамической погрешности. Расчет этой погрешности осуществляют методами теории чувствительности.

Пусть при номинальных значениях параметров, сигнал на выходе системы равен yo (t) . Предположим, что значение одного из параметров отклоняется от

номинального значения на величину α, при этом выходной сигнал будет функцией как времени, так и α

y = y(t, α) ,

(7.16)

а динамическая погрешность, обусловленная отклонением параметра, определится из выражения

yдин = y(t, α) − yo (t) ,

(7.17)

Разложим функцию (7.16) в ряд Тейлора по степеням параметра α

∂y(t, α)

∂2 y(t, α)

α2

y(t, α) = yo (t) +

α +

+....

(7.18)

∂α

∂α

2

2

α=0

α=0

Коэффициенты при α называют функциями чувствительности.

z

I

∂y(t, α)

, z

II

(t, 0)

∂2 y(t, α)

, …

(7.19)

(t, 0) =

∂α

=

∂α

2

α=0

α=0

Тогда динамическую погрешность (7.17) с учетом (7.18) и (7.19) можно записать в виде

yдин = z I (t, 0) α + z II (t, 0)	α2	+....	(7.20)
	2

Если α мало, то для практических целей можно ограничиться первым слагаемым функции (7.20):

yдин = z I (t, 0) α.

(7.21)

Из выражений (7.20), (7.21) следует, что функции чувствительности характеризуют влияние отклонения параметра α на изменение выходного сигнала.

Заметим, что аналогом zI (t, 0) при переходе к статическому режиму работы прибора является коэффициент влияния (∂ f ∂qs )qS O в формуле (5.13).

Таким образом, зная выражение для выходного сигнала y(t, α) , можно путем

его дифференцирования и приравнивания α к нулю непосредственно определить функции чувствительности по выражениям (7.19).

Можно функции чувствительности определить и через передаточную функцию прибора.

87

Пусть измерительная цепь описывается передаточной функцией W ( p) , тогда с учетом α передаточная функция примет вид W ( p, α) . Согласно преобразованию Лапласа

y( p, α) =W ( p, α) x( p) .

В этом случае оригинал выходного сигнала можно определить с использованием обратного преобразования Лапласа

y(t, α) = L−1[W ( p, α) x( p)].

Дифференцируя последнее равенство по α и приравнивая α к нулю, определим значения функций чувствительности:

	z	I		−1		∂W ( p, α)			,	(7.22)
			(t, 0) = L			∂α		x( p)
							α=0
						2
	II			−1	∂ W ( p, α)
z		(t, 0)						x( p) , …		(7.23)
				= L		∂α2
							α=0

Пример 7.2. Апериодическое звено.

Определим динамическую погрешность апериодического звена, вызванную отклонением постоянной времени от номинального значения, при входном сигнале в виде единичного скачка.

Передаточная функция апериодического звена имеет вид

W ( p) = Tp1+1,

где T – постоянная времени рассматриваемого звена. Изображение входного сигнала в виде скачка имеет вид

x( p) =1 p .

Тогда изображение выходного сигнала можно определить из выражения

y( p) =W ( p) x( p) =			1		,
			(Tp +1)p
а оригинал выходного сигнала
−1	1			−t T
y(t) = L			=1 − e			.
	(Tp +1)p

Пусть постоянная времени T увеличилась на величину α: Tα = T + α.

Определим динамическую погрешность, возникающую в результате этого изменения. Измененная передаточная функция имеет вид

	Wα( p) =	1		.
		(T + α)p +1

Найдем функцию чувствительности в соответствии с выражением (7.22):

88

∂

1

1

t

I

−1

1

−1

−t T

z

(t, 0) = L

= L

−

= −

e

.

(T + α)p +1

(Tp +1)2

T

∂α

α=0

p

Тогда искомая функция динамической погрешности определяется согласно выражению (7.21):

yдин = − αTt e−tT .

Методы теории чувствительности могут быть применены также и для случайных отклонений параметров от номинальных значений. Пусть α есть случайная величина с математическим ожиданием M[α] и среднеквадратическим отклонением σα . Применим операцию математического ожидания к выражению

(7.21) и получим

M [ yдин]= z I (t, 0) M[α].

Найдем дисперсию выражения (7.21)

D[ yдин]= (z I (t, 0))2 σ2α ,

следовательно, среднеквадратическое отклонение динамической погрешности σ yдин равно

σ yдин = D[ yдин]= z I (t, 0) σα .

Заметим, что теория чувствительности позволяет получить приближенное решение, когда изменения параметра сравнительно малы. Однако для практических инженерных расчетов такая точность, как правило, является достаточной.

7.4. Расчет динамической погрешности при возмущающих воздействиях, ограниченных по модулю

Оценим влияние возмущающих факторов на измерительный прибор, работающий в динамическом режиме. На практике часто о возмущениях, действующих на объект, имеется очень мало априорной информации. В этом случае основываются на предположении о максимально возможном значении воздействий, то есть ограничивают воздействие по модулю.

При такой постановке задачи расчета точности ее решение выполняют в два этапа:

–определение наиболее неблагоприятного из возможных видов воздействия, вызывающего наибольшее отклонение сигнала на выходе прибора;

–определение динамической погрешности прибора при найденном наиболее неблагоприятном виде воздействия.

Пусть возмущающее воздействие η(t) ограничено по модулю некоторым

значением L:

89

	η(t)		≤ L.	(7.24)

Требуется из множества возможных функций η(t) , удовлетворяющих условию

(7.24), найти наименее благоприятный вариант функции, приводящий к максимально возможной динамической погрешности, и вычислить это максимальное значение погрешности.

При неизменном входном сигнале x(t) = const искомое значение вынужденной динамической погрешности будет определяться величиной выходного сигнала, вызванного возмущающим воздействием η(t) . Выходной сигнал можно определить с помощью интеграла свертки

t
y(t) = ∫η(t − τ) h(τ)dτ.	(7.25)
0

Согласно данной формуле определяется максимальное отклонение, накопленное за интервал времени от 0 до t. Преобразуем (7.25) с учетом (7.24):

t t

y(t) ≤ ∫ η(t − τ) h(τ) dτ ≤ L ∫ h(τ)dτ.

0 0

Следовательно, искомое максимально возможное отклонение будет достигаться при таком входном сигнале h(t), при котором η(t − τ) = L , если h(τ) > 0 и η(t − τ) = −L если h(τ) < 0 .

Таким образом,

t

ymax (t) = L∫ h(τ)dτ.

0

Если взять верхний предел интегрирования равным бесконечности, то можно найти предел максимально возможного значения выходного сигнала (динамической погрешности)

lim[ymax (t)]= L∞∫			h(τ)		dτ.	(7.26)
t→∞	0

График функции (7.26) называется кривой накопления Булгакова. Ее можно построить, если известна переходная характеристика u(t).

h(t) = dud(ττ) .

На рис. 7.1 показан пример построения кривой накопления Булгакова. На участке от 0 до τ1 выполняется неравенство du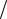dτ > 0 , поэтому кривая накопления

совпадает с переходной характеристикой. На интервале от τ1 до τ2 наблюдается dudτ < 0 , поэтому участок BC* получается зеркальным отображением участка

BC. На интервале от τ2 до τ3 имеет место dudτ > 0 , поэтому участок C*D*

получился путем параллельного переноса участка CD переходной характеристики. Дальнейшее построение осуществляется аналогично.

90