§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях

В параметрической системе может существовать как свободные, так и вынужденные колебания.

Пусть мы рассматриваем цепь с переменными параметрами, но изменение параметров проходит очень медленно (за период колебания изменение параметров очень малое, аналогично и в длинных линиях изменение параметра малое на длине волны).

Считаем, что на протяжении какого-то малого промежутка времени ∆t в момент времени t₀, параметры постоянные (замороженные). Тогда мы можем найти выходное колебание обычным операторным методом – . После того, как мы «размораживаем» параметры, не только выходной сигнал становится зависимым от времени, но и параметрыL(t), C(t), R(t) и G(t) также становятся зависимыми от t:

. (2.100)

Этим методом нельзя проанализировать параметрическое усиление и генерацию, т.к. в этих задачах частота накачки выше частоты изменения сигнала.

а) Система с сосредоточенными параметрами (например, радиотехническая цепь). Задача анализа свободных колебаний

Уравнение, описывающее колебания в параметрической цепи, можно записать в виде системы интегродифференциальных уравнений (например, для МКТ) в следующем виде: .

Пусть скорость изменения параметров здесь намного меньше, чем частота колебаний сигнала, тогда можно записать:

.

Здесь мы «заморозили» параметры, т.е. считаем, что они имеют постоянную величину, которую они имели в момент времени t=t₀. Все коэффициенты системы интегродифференциальных уравнений будут постоянными, поэтому для решения этой системы уравнений можно применить операторный метод:

.

Мы получили систему алгебраических уравнений, из которой найдем выходное колебание используя формулы (1.24-1.25)

.

«Размораживание» можно сделать как сейчас, так и после обратного преобразования Лапласа.

или

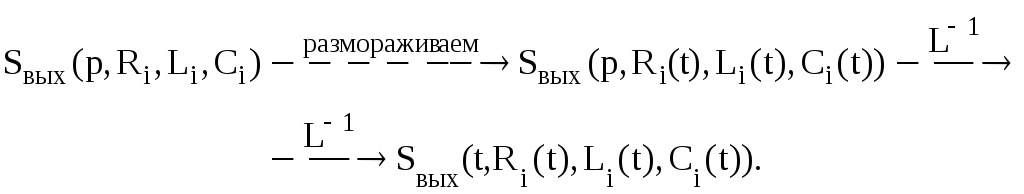
Мы получили, что выходное колебание зависит не только от явно содержащегося времени t, но и через параметры . Полученный результат свидетельствует о том, что в данной цепи при возникновении свободных колебаний возбудятся все гармоники основного колебания.

б) Система с сосредоточенными параметрами (например, радиоцепь). Анализ происхождения сигнала

Пусть у нас имеется радиоцепь. И пусть выполняется основное условие применимости метода «замороженного» параметра – изменение параметра просходит значительно медленнее, чем скорость изменения входного сигнала, прохождение которого через радиоцепь исследуется. Предположим, что для составления системы уравнений или одного уравнения (в зависимости от количества независимых контуров или независимых узлов), удобно применить метод контурных токов МКТ. В соответствии с аксиоматикой запишем систему интегро-дифференциальных уравнений:

.

Так как параметр меняется медленно, можно считать его в некоторый момент времени t₀ постоянным – «замороженным». Тогда все коэффициенты матрицы станут постоянными (не зависящими от времени). Тогда к системе интегродифференциальных уравнений можно применить операторный метод. Применение операторного метода позволит преобразовать систему интегро-дифференциальных уравнений в алгебраическую систему уравнений, алгоритм решения которой дано в первой главе. Получив, операторно-передаточную функцию радиоцепи найдем, выходное колебание в виде (2.101). Ниже представлен алгоритм нахожденя выходного колебания методом «замороженного» параметра. Полученный результат позволит исследовать изменение спектрального состава входного колебания при прохождении его через параметрическую радиоцепь. Этапы алгоритма построения решения для задачи о вынужденных колебаниях в параметрической системе представлены формулой (2.101):

(2.101)

в) Система с распределенными параметрами (например, длинная линия,параметры которой медленно изменяются в пространстве,например, вдоль координаты x)

Пусть у нас погонные параметры зависят от координаты х (рис.2.34): , тогда:

Рис.2.34. Параметрическая система с распределенными параметрами

по координате х

Используя формулу (1.38) с учетом того, что погонные прарметры стали зависить от координаты сечения линии х, запишем дифференциальныеные уравнения в следующем виде:

. (2.102)

Система уравнений (2.102) должна быть дополнена начальными и граничными условиями. Для упрощения построения решения, будем считать, что начальные условия у нас нулевые. Если параметры меняются медленно по сравнению с частотой распространяющейся волны вдоль длинной линии, тогда применим метод «замороженного» параметра. В соотвествии с методикой построения решения считаем, что параметры у нас в некоторой точке координаты х₀ на протяжении небольшого интервала переменной ∆х постоянными, т.е. «замороженным»:получим систему уравнений длинных линий с постоянными коэффициентами (см. формулу 1.41)(применяем преобразование Лапласа к полученной системе уравнений с постоянными коэффициентами), получаем систему алгебраических уравнений в операторной форменаходим решение для операторного тока и напряжения

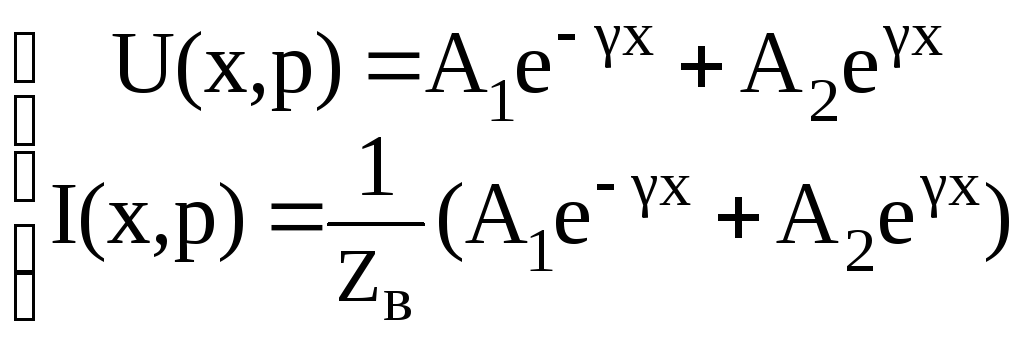
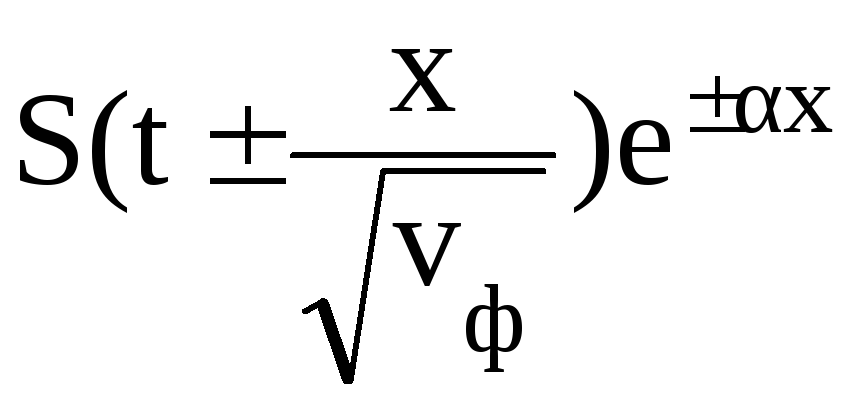
ограничимся в дальнейшем линиями без потерь или без искаженийрешение в таких линиях имеет вид бегущих волнпосле «размораживания» параметров, они становятся функциями координаты х и решение получаем в следующем виде:

. (2.103)

Преобразование частотного спектра здесь не происходит. Происходит обогащение колебания пространственными гармониками.

г) Система с распределенными параметрами в длинных линиях, параметры которых изменяются во времени

Пусть у нас погонные параметры зависят от времени R(t), C(t), L(t), G(t).

Все аналогично предыдущему случаю, но мы получаем теперь решение в виде бегущих волн: . Причем операторно-передаточная функцияимеет вид:

. (2.104)

Зависимость погонных параметров от времени приводит к тому, что операторно-передаточная функция T(p,t) зависит теперь от р и t через зависимость параметров от времени t. Следовательно, это приводит к появлению в спектре передаточной функции цепи новых комбинационных частот.

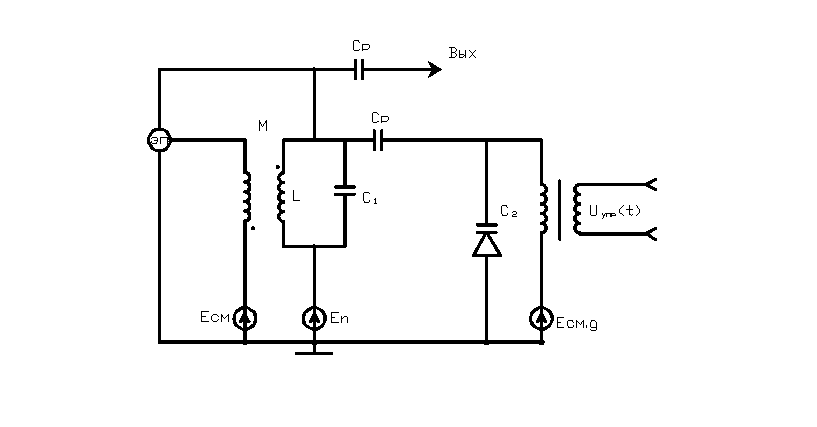Пример 2.8. Методом «замороженного» параметра исследовать процесс частотной модуляции в автогенераторе с варикапом в колебательной системе (рис.2.35).

Рис.2.35. Автогенератор с варикапом в колебательной системе

Для того, чтобы получить частотно модулированное колебание, дастаточно взять генератор гармонических колебаний, у которого частота будет изменяться по заданному закону. В самом общем случае, варикап − это нелинейный полупроводниковый прибор, у которого емкость меняется по закону (рис.2.36) C(U)=φ(U). Однако, если приложенное к варикапу управляющее напряжение U_упр(t) мало (оно не выходит из линейной области изменения C(U)), тогда С(t) изменяется по закону приложенного напряжения U_упр(t). Следовательно, в этом случае, варикап может использоваться как параметрическая емкость (рис.2.35). Поэтому, когда изменение управляющего напряжения не выходит за линейную область вольткулоновской характеристики:

C₂(t) C₂₀ + ∆C cos Ωt. (2.105)

В случае любой модуляции несущая частота значительно больше частоты модуляции, то выполняется основное условие применимости метода замороженного параметра Ω ‹‹ ω_р .

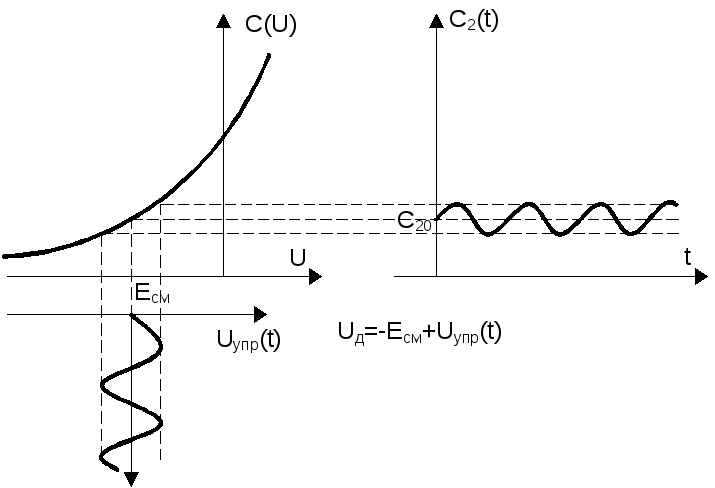
2.36. Изменение емкости варикапа при заданном U_упр(t)

Применим метод «замороженного» параметра для исследования схемы представленной на рис.2.35. Считаем что все элементы цепи стали постоянными и емкость варикапа C₂(t)=const. Теперь емкость колебательного контура будет состоять из двух параллельно включенных емкостей С₁ и С₂ (рис.2.37).

Так как у нас теперь схема автогенератора состоит из всех постоянных элементов, то в соответвствии с результатами теории линейных цепей, можем записать, что

U_вых = U₀ cos(ω_рt + φ₀) = U₀ cosψ(t). (2.106)

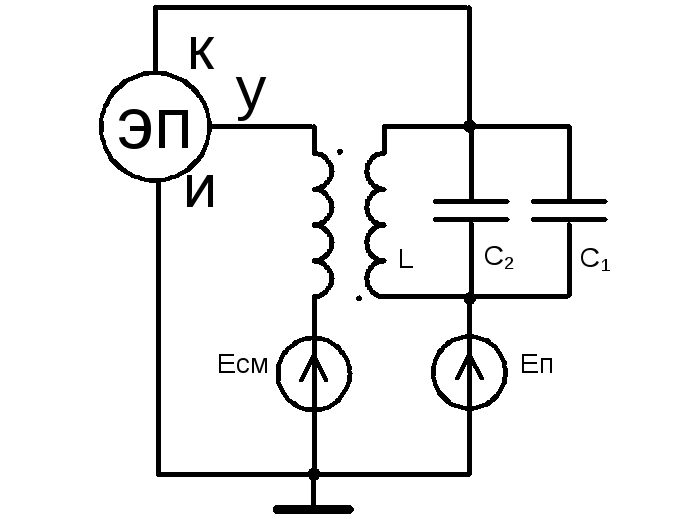
Рис.2.37. Эквивалентная схема автогенератора, у которой варикап

представлен постоянной емкостью С₂

Пусть у нас управляющее напряжение, которое подается на варикап, изменяется по закону:

U_упр = U_у cos Ωt.

Применим алгоритм метода «замороженного» параметра для нахождения выходного колебания в нашем автогенераторе.

резонансная частота автогенератора определяется элементами резонансного колебательного контура и может быть записана в следующем виде ω_{p =}

после «размораживания» емкость С₂=С₂(t) стала зависить от времени и определяется формулой (2.105). Поэтому:

ω_р(t) = =

= = ,

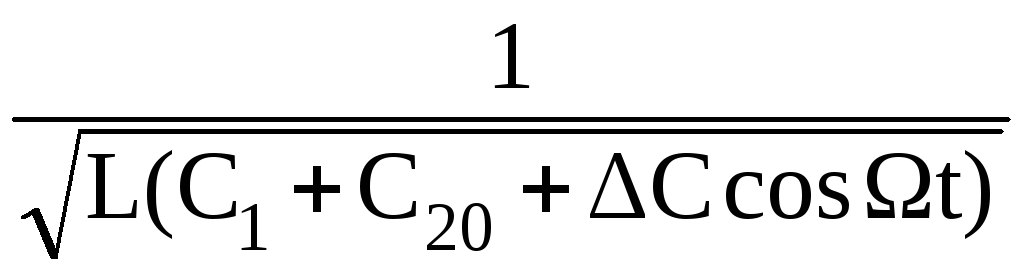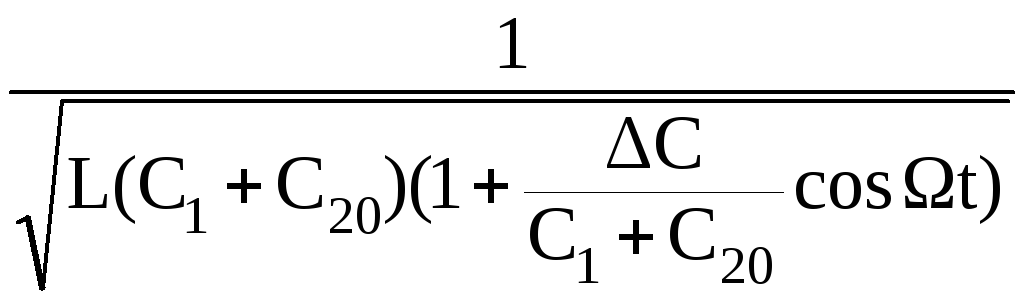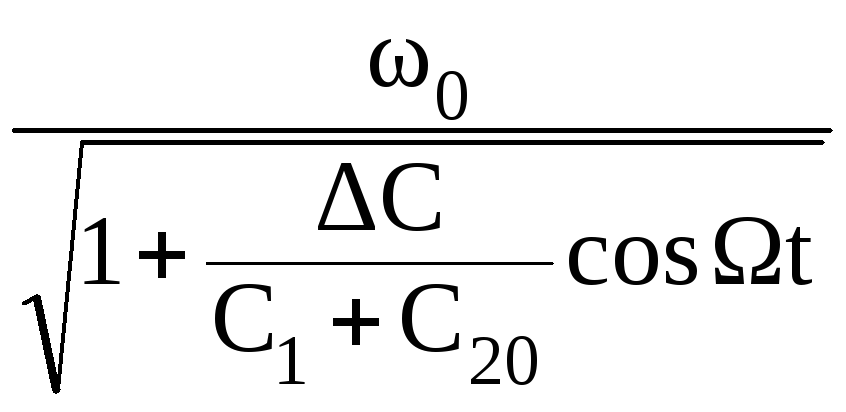где введено обозначение ω₀ = 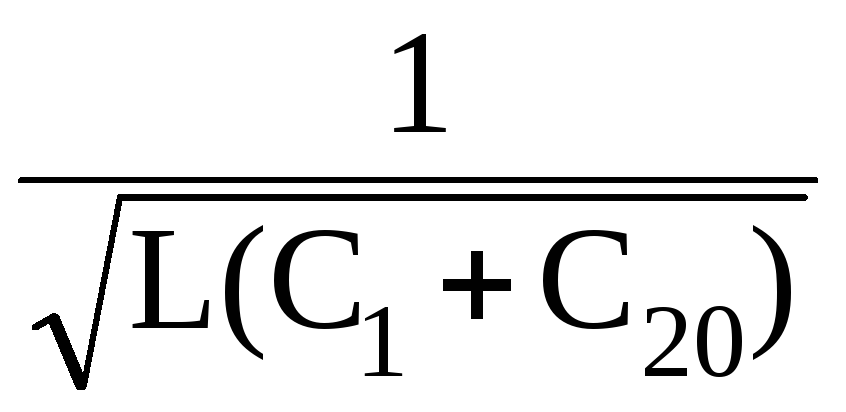- несущая частота,

т.к. ∆С ‹‹ (С₁ + С₂₀), то ω_р(t) = ω₀(1 – ε(t)) – мгновенная частота колебаний автогенератора, а ε(t) = .

При выводе выражения для ω_р(t) использовалось разложение в ряд Тейлора функции , в котором учтено, что.

Мгновенная частота связана с полной фазой колебаний соотношением:

ω(t) = ; или.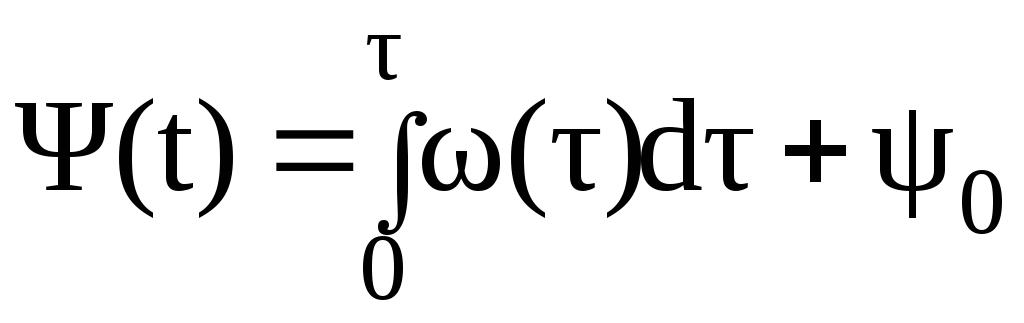

Следовательно, для нашего случая, полная фаза колебаний автогенератора определяется соотношением:

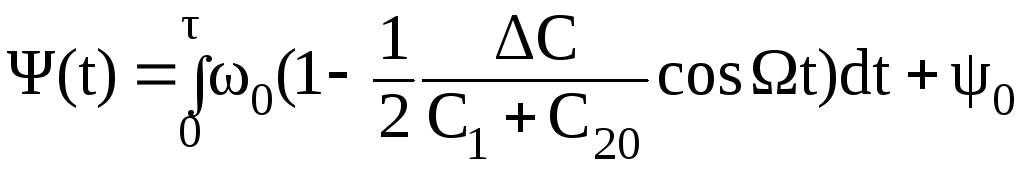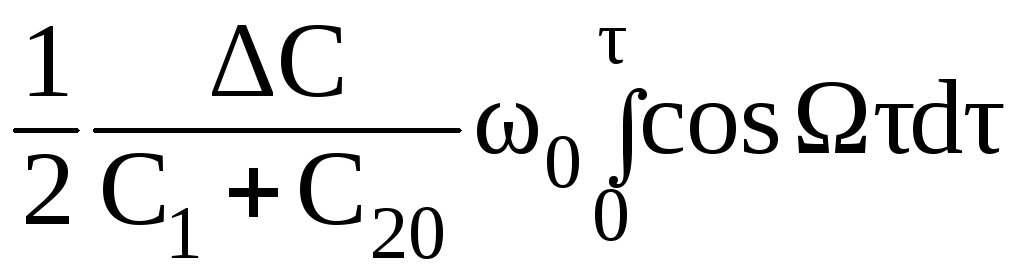= ω₀t – + ψ₀ =

=ω₀t – ω_{0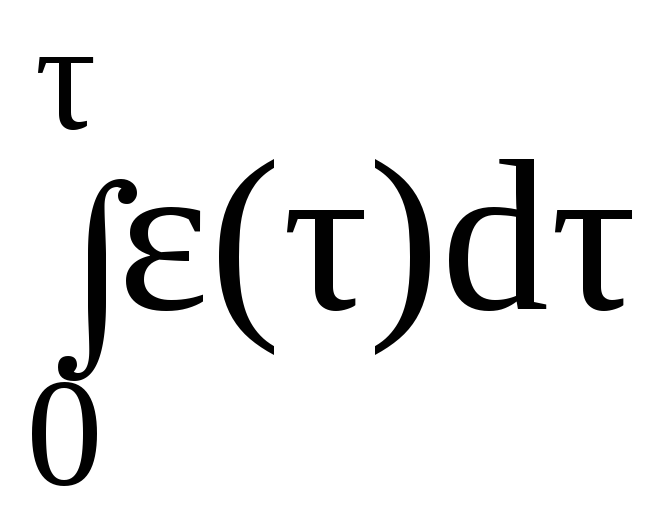 +} ψ_{0 .} (2.107)

Теперь мы можем подставить найденное выражение (2.107) для полной фазы в выражении (2.106), определяющее выходное напряжение.

U_вых(t) = U_чм(t) = U₀ cosψ(t) = U₀ cos(ω₀t + =

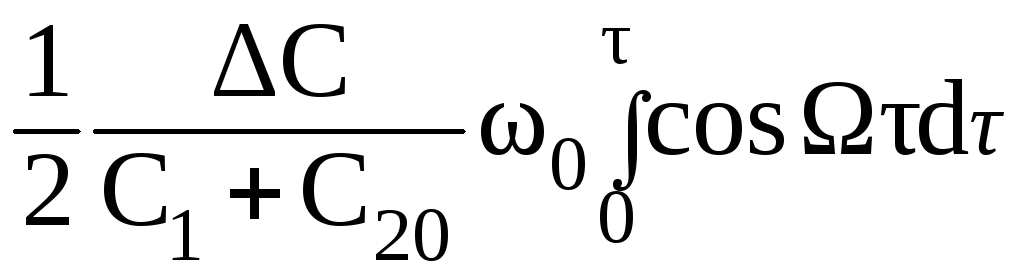=U₀ cos (ω₀t – ω_{0 +} ψ₀ ) . (2.108)

Замечание: вместо управляющего сигнала, изменяющегося по закону cos Ωt, может быть любая функция для управляющего напряжения, т.к. при выводе выражения (2.108) мы не делали никаких предположений относительно закона изменеия ε(t):

U_вых (t) = U₀ cos (ω₀t + a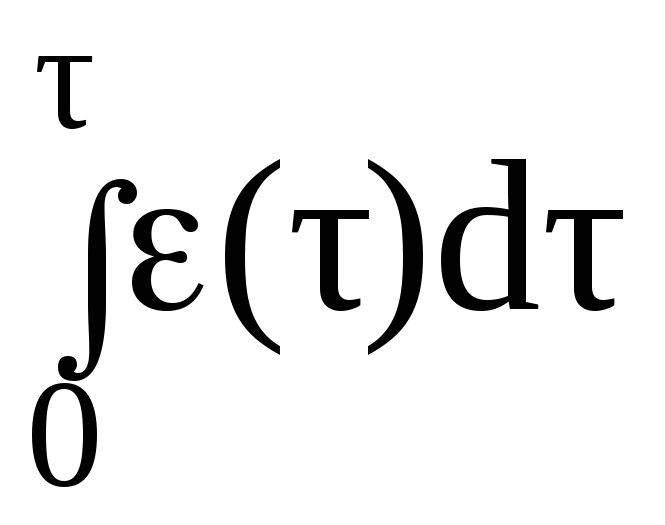+ ψ₀ ).

Как видно из приведенной задачи, метод «замороженного» параметра с помощью простейших вычислений позволил получить закон изменения выходного колебания в схеме рис.2.35 с частотной модуляцией.