§3.11.2.Исследование методом фазовой плоскости схемы на

туннельном диоде

Проиллюстрируем один из вариантов метода фазовой плоскости на примере анализа цепи с туннельным диодом.

а) б)

Рис.3.64. Схема автогенератора на туннельном диоде (а) и его

эквивалентная схема (б)

Система уравнений для схемы рис.3.64.а имеет вид:

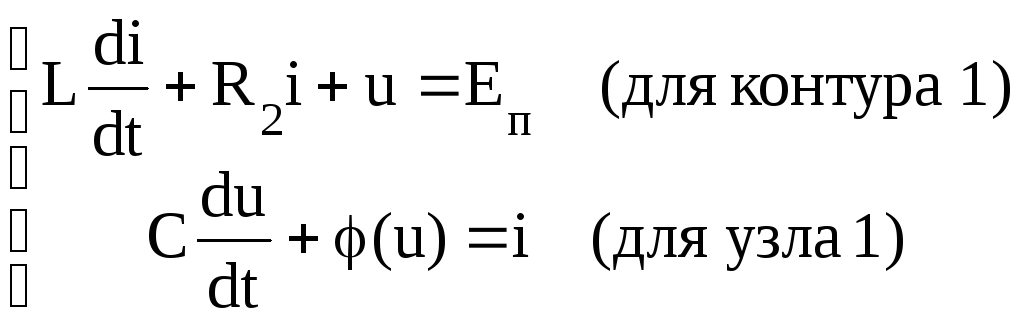. (3.123)

Подставляя второе уравнение в первое, получим

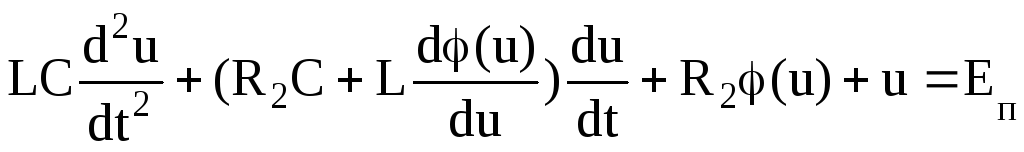. (3.124)

Аппроксимируем вольтамперную характеристику туннельного диода φ(u) следуюшим рядом

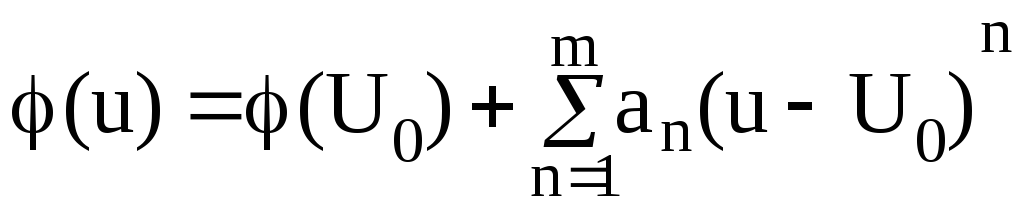. (3.125)

Пусть рабочая точка на вольтамперной характеристике выбрана на середине падающего участка, а U₀ – постоянная составляющая, соответствующая выбранной рабочей точке. Обозначим через - переменную составляющую нарапряжения. Будем считать, что у нас возможно либо одна, либо три точки пересечения с ВАХ туннельного диода (рис.3.65).

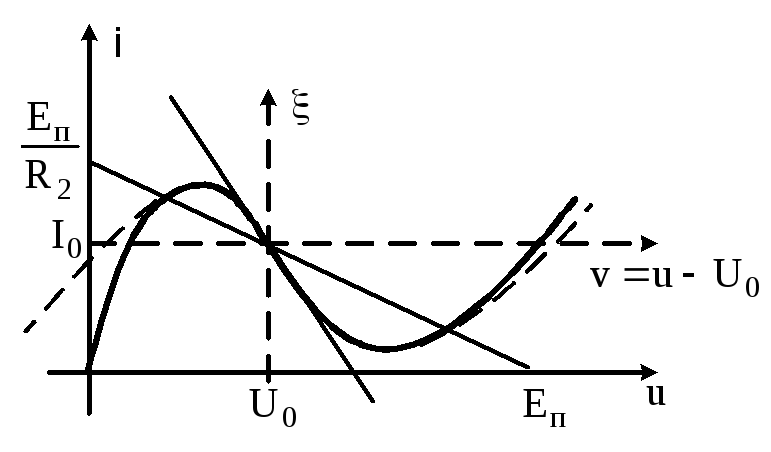
Рис.3.65. ВАХ туннельного диода и расположение точки покоя на ВАХ

Уравнение, определяющее точки покоя, вытекакет из равенства (3.124), если приравнять нулю первую и вторую производные от u:

.

Тогда, обозначая и учитывая, что, находим что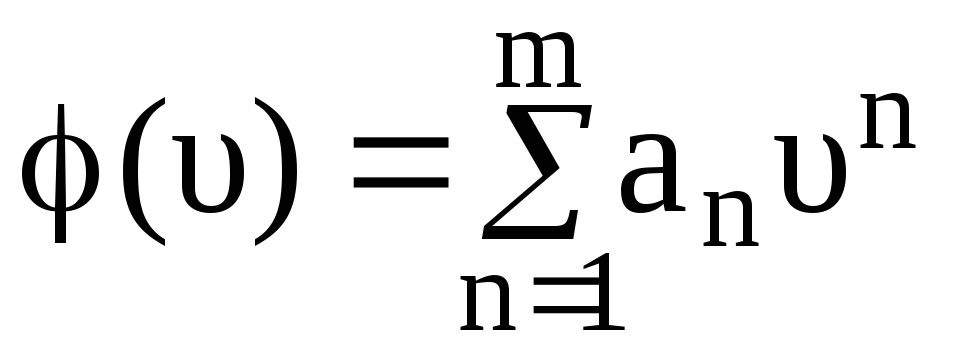, а уравнение цепи (3.124) запишем в виде

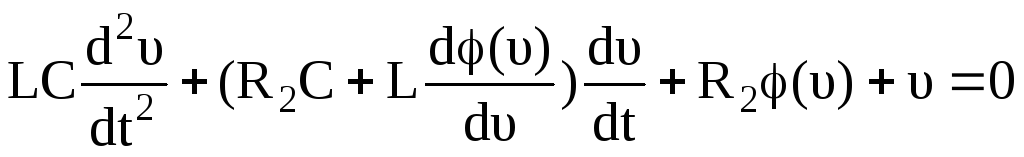. (3.126) Введем безразмерное время τ: и приведём уравнение к виду

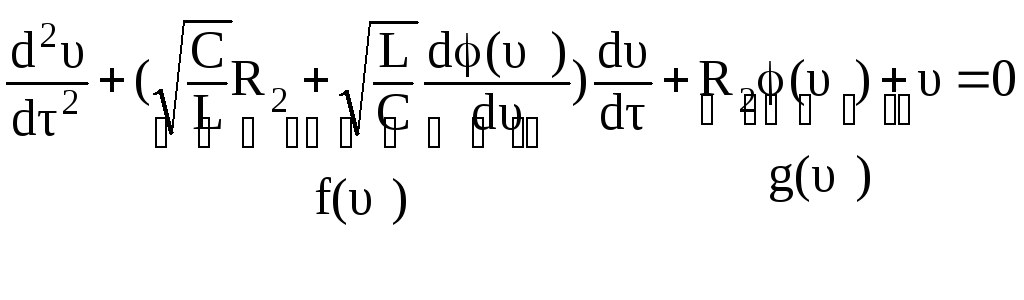, (3.127)

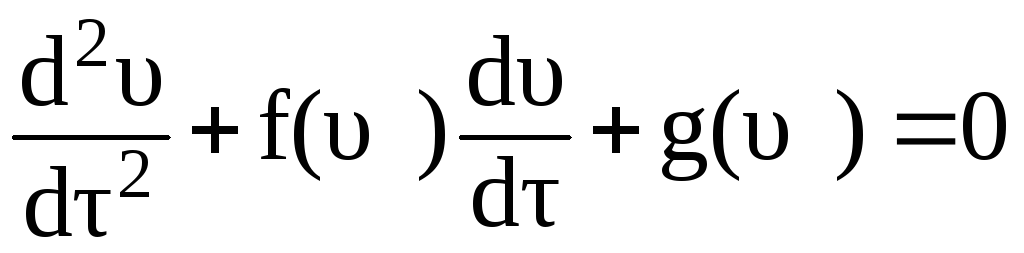. (3.128)

Перейдём к уравнениям, позволяющим определить фазовые портреты вокруг особых точек. Обозначим

, (3.129)

тогда из уравнения (3.127) получаем

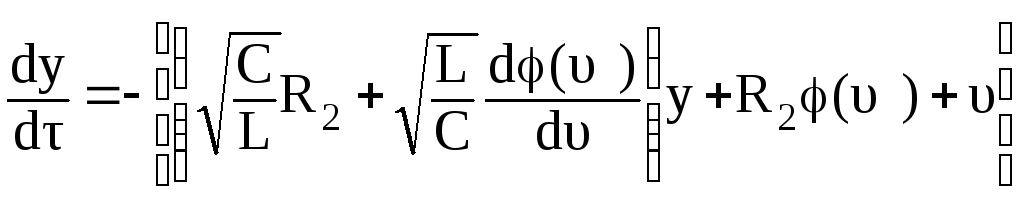. (3.130)

Делим второе уравнение на первое и тогда получим уравнение вида

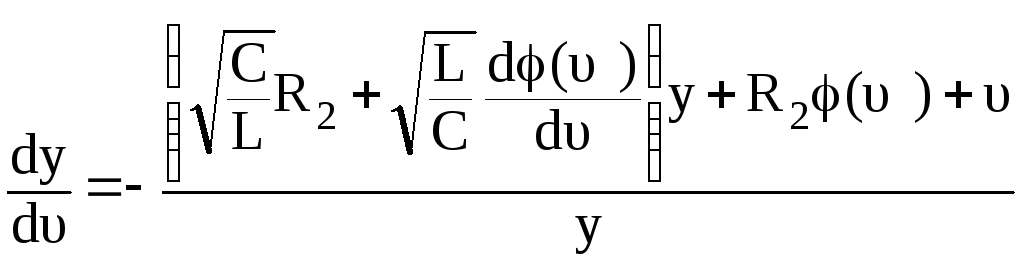, (3.131)

которое описывает все интегральные кривые на фазовой плоскости величин иy.

Особые точки на фазовой плоскости удовлетворяют уравнениям

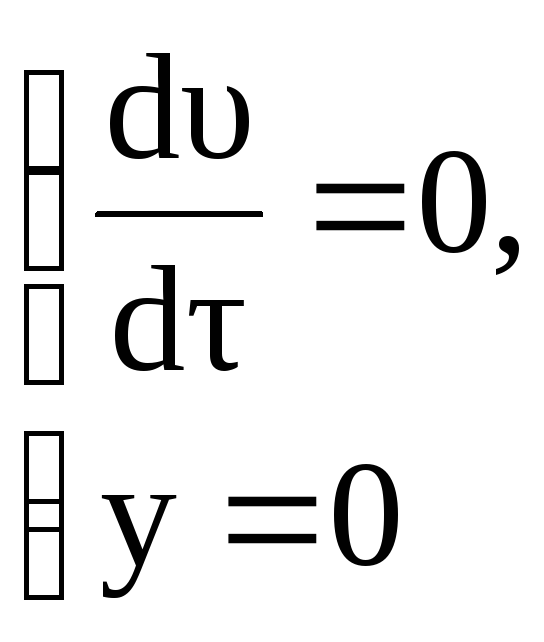(3.132)

т.е. все особые точки в рассматриваемом случае располагаются на оси абсцисс . Если

,

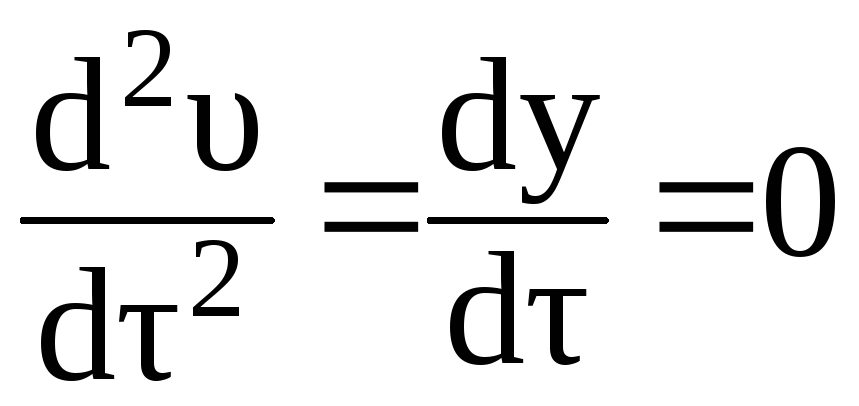тогда из уравнения (3.131) находим

, (3.133)

откуда, с учётом того, что y=0, получаем

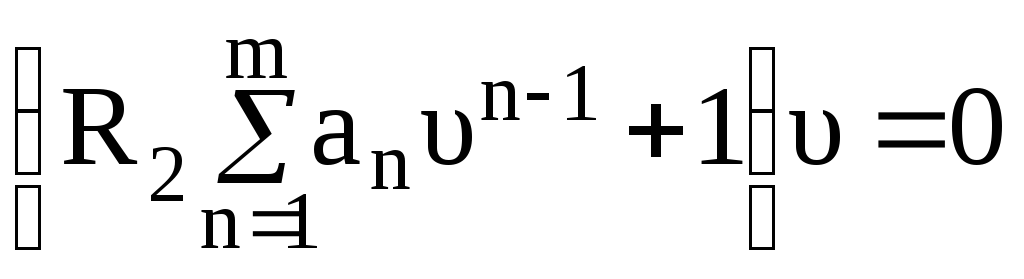или . (3.134)

Т.е. одна особая точка располагается в начале системы координат y₁=0; =0. Для определения координат остальных особых точек следует решить уравнение вида

.

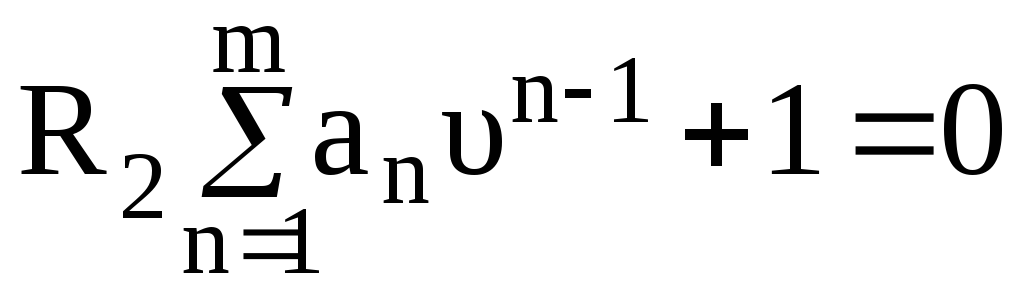Пусть, например, ВАХ туннельного диода аппроксимируется полиномом третьей степени вида

,

тогда

(3.135)

- знакомый по предыдущим параграфам вид аппроксимирующего полинома.

Следовательно, уравнение (3.134) для определения координат особых точек примет вид:

. (3.136)

Откуда находим, что и(рис.3.66), причём для существования этих особых точек необходимо, чтобы>0.

Рис.3.66. Расположение корней уравнения (3.136) на фазовой плоскости

координат

Исследуем окрестности особых точек. Пусть у нас выполняется условие, что <0. Это значит, что в этом случае у нас только одна особая точка с координатами v=0 и y=0. Для определения типа особой точки, зададим малое отклонение от нее v=v₁+ξ₁, т.е. произведем линеаризацию уравнения (3.127). С учетом равенства (3.135) получим для малых отклонений:

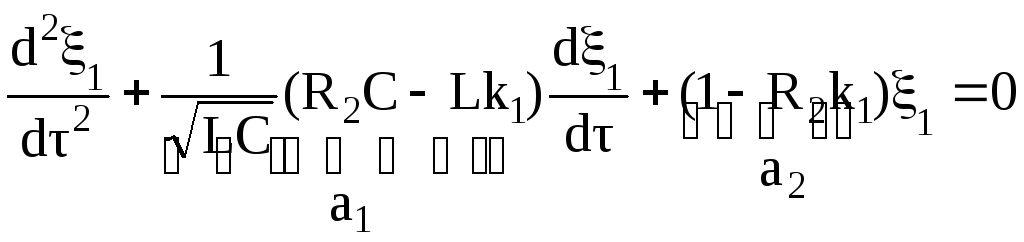. (3.137)

Т.к. мы рассматриваем случай, когда <0, то коэффициент а₂>0. Следовательно, можно сделать вывод, что наша особая точка не может быть седлом.

Случай 1. Пусть параметры схемы (рис.3.64) такие, что коэффициент а₁>0, т.е. , а корни характеристического полинома

р² + а₁р + а₂ = 0, (3.138)

имеют вид

,

т.е. представляют собой пару комплексно сопряженных корней. Поэтому в соотвествии с таблицей 3, особая точка является устойчивым фокусом, а фазовые траектории предсталены на рис.3.67.б. Схема (рис.3.64) в этом случае представляет собой регенеративный усилитель.

Случай 2. Пусть параметры схемы рис.3.64 такие, что коэффициент а₁>0, т.е. , а корни характеристического полинома

р² + а₁р + а₂ = 0, (3.138)

имеют вид

.

Таким образом, мы получаем, что особая точка − устойчивый узел, а фазовые портреты представлены на рис.3.67.а.

Фазовые портреты для случая <0 и >0 имеют вид либо устойчивый узел (рис. 3.66.а), либо устойчивый фокус (рис.3.66.б):

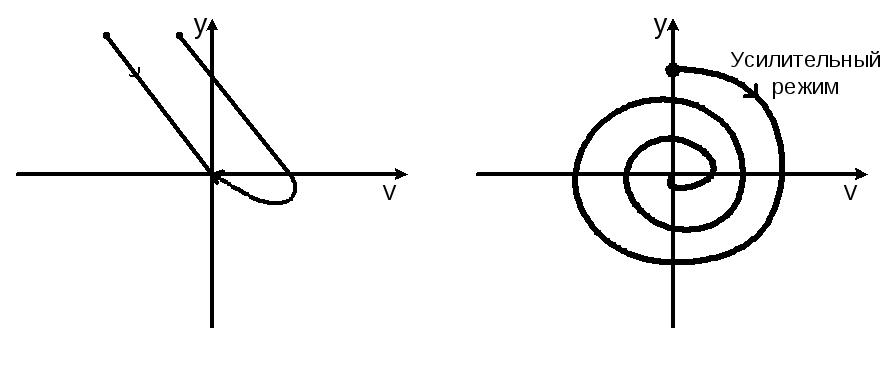
а) б)

Рис.3.67. Фазовые портреты схемы (рис.3.64) при <0 и

>0 – устойчивый узел (а) и устойчивый фокус (б)

Случай 3. Пусть параметры схемы рис.3.64 такие, что коэффициент а₁<0, т.е. , а корни характеристического полинома

р² + а₁р + а₂ = 0,

имеют вид

,

т.е. представляют собой пару комплексно сопряженных корней с положительной действительной частью. Поэтому в соотвествии с таблицей 3, особая точка является неустойчивым фокусом, а фазовые траектории предсталены на рис.3.68. Схема (рис.3.64) в этом случае представляет собой автогенератор гармонических колебаний.

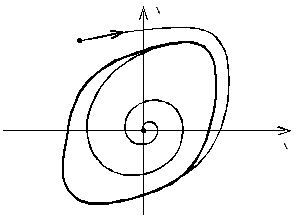
Рис.3.68. Фазовый портрет автогенератора гармонических колебаний –

неустойчивый фокус

Случай 4. Пусть параметры схемы (рис.3.64) такие, что коэффициент а₁<0, т.е. , а корни характеристического полинома

р² + а₁р + а₂ = 0,

имеют вид

,

т.е. представляют собой пару действительных положительных корней. Поэтому в соотвествии с таблицей 3, особая точка является устойчивым узлом, а фазовые траектории предсталены на (рис.3.69). Схема рис.3.64 в этом случае представляет собой автогенератор апериодических колебаний − мультивибратор.

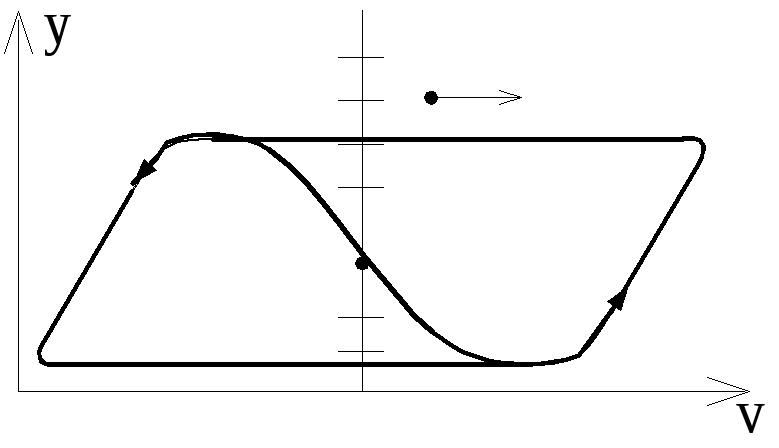
Рис.3.69. Фазовый портрет автогенератора апериодических колебаний –

неустойчивый фокус

В обоих случаях 3 и 4 неустойчивого фокуса или неустойчивого узла, когда <, для неустойчивой особой точки на фазовой плоскости обязан существовать предельный цикл, поскольку вследствие конечности энергии источникаамплитуда колебаний не может достигать бесконечно больших значений. Причём раскачке колебаний соответствует область, вблизи 0, установившимся колебаниям соответствует предельный цикл, который будет устойчивым.

Случай 5. Рассмотрим случай когда, >0, коэффициент а₂<0. Следовательно, можно сделать вывод, что наша особая точка − седло.

Таким образом, на фазовой плоскости имеются три особые точки. Первая с координатами существует при любых параметрах цепи, вторая и третья с координатам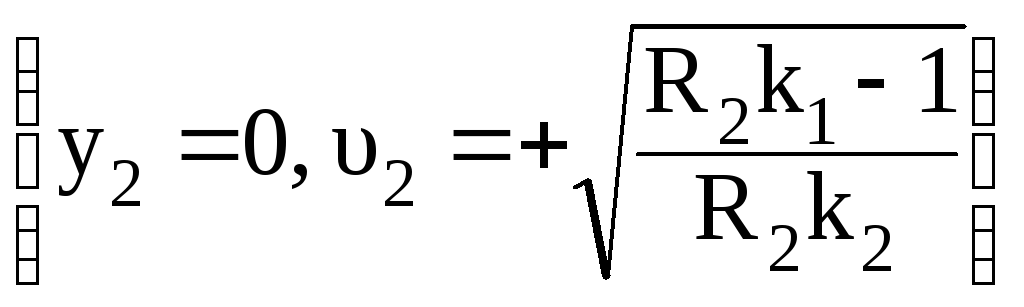и и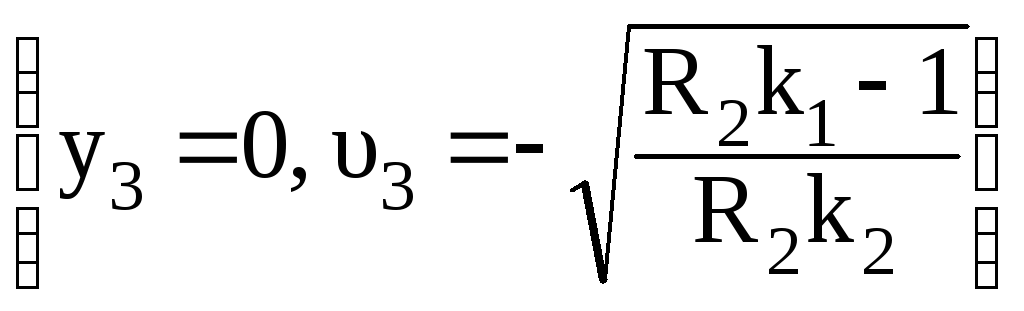существуют только при условии, что>0, т.е.R₂ > R_1диф (рис.3.70).

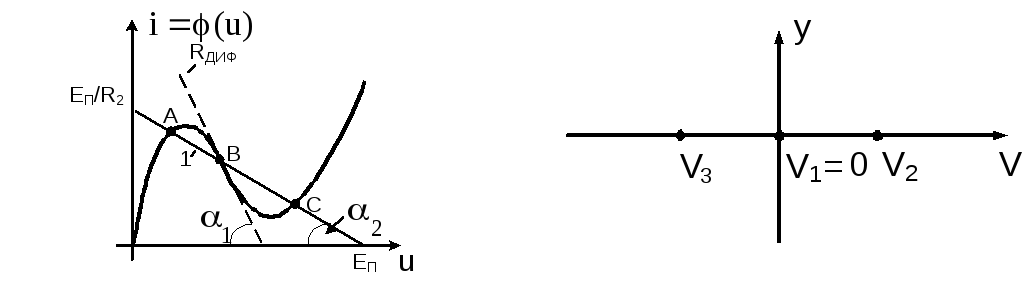
а) б)

Рис. 3.70. ВАХ туннельного диода (а) и расположение особых точек на

фазовой плоскости для случая >0 (б)

Возвращаясь к исходному уравнению (3.127), с учетом равенства (3.135), получаем

. (3.139)

Рассмотрим поведение интегральных кривых в окрестностях второй и третей особых точек

; .

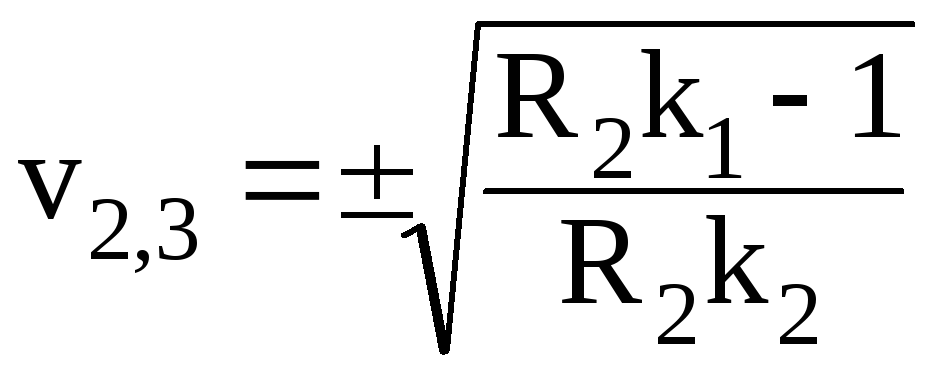Для рассмотрения характера поведения систем вокруг особых точек зададим малые отклонения от положения особой точки, пусть . Подставляя последнее соотношение в уравнение (3.139) находим

.

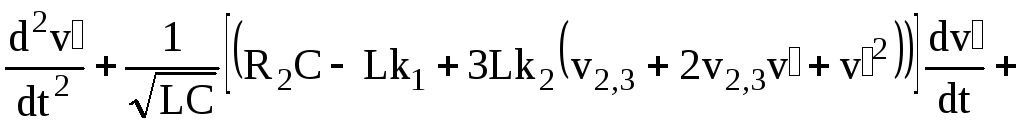
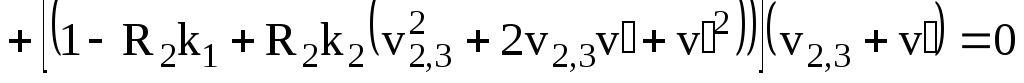Первые три слагаемых во второй скобке равны нулю:

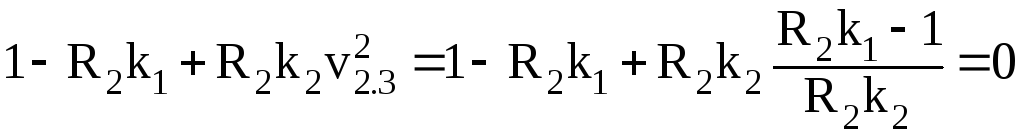
Учитывая, что малое отклонение от особой точки − , получаем

,

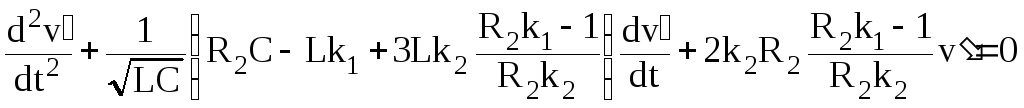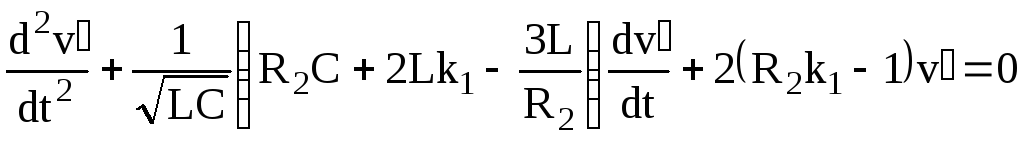. (3.140)

Уравнение (3.140) является линеаризованным уравнением для малых отклонений. Поэтому коэффициенты характеристического уравнения (3.138) будут равны

. (3.141)

Замечаем, что по условию существования корней, , поэтому а₂>0 для этих особых точек. Следовательно, первая особая точка обязательно седло, вторая и третья особые точки обязательно не седла. При а₁>0 эти две особые точки могут быть либо устойчивый фокус, либо устойчивый узел. Особая линия сепаратрисса, порожденная седлом, разделяет фазовую плоскость на 2 области притяжения к устойчивым особым точкам 2 и 3 (рис.3.71).

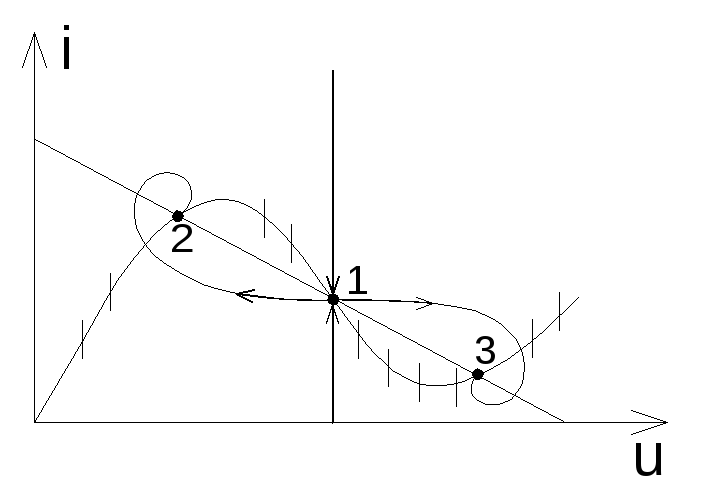
Рис.3.71. Характер поведения колебаний для случая, когда вторая и

третья особые точки есть устойчивый узел

На рис. 3.71 показан характер поведения схемы (рис.3.64) для случая, когда корни характеристического полинома являются действительными отрицательными величинами. Особые точки два и три в этом случае являются особыми точками − устойчивый узел. Схема (рис.3.64) в данном случае есть триггер.

Если же корни характеристического полинома − пара комплексно сопряженных корней с отрицательной действительной частью, то особая точка есть устойчивый фокус, а фазовые портреты представлены на (рис.3.72).

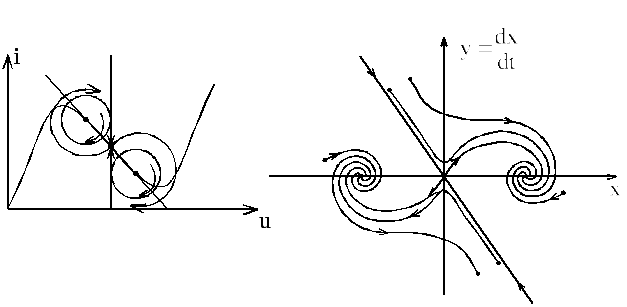Данная схема представляет собой плохой триггер, у которого присутствуют паразитные реактивные элементы L и C − триггер с дребезгом, т.е. установление устойчивого состояния, происходит в виде экспоненциально затухающих гармонических колебаний.

Рис.3.72. Фазовые портреты схемы (рис.3.64) для случая когда

коэффициенты а₁>0 и а₂>0 для особых точек 2 и 3.

Если ВАХ туннельного диода, позволит провести нагрузочную линию таким образом, что она пересечет ее в трех точках, которые будут располагаться все на падающем участке ВАХ, тогда для всех трех особых точек R_диф<0. Поэтому первая особая точка останется − седлом, а вторая и третья особые точки могут быть неустойчивыми особыми точками − неустойчивый фокус (рис.3.73).

На фазовом портрете жирным цветом выделены две особые линии: сепаратриса и два предельных цикла, вокруг каждой из особой точки.

Сравним полученные результаты с результатами полученными ранее:

а) В методе линеаризации мы получили, что рабочая точка по постоянному

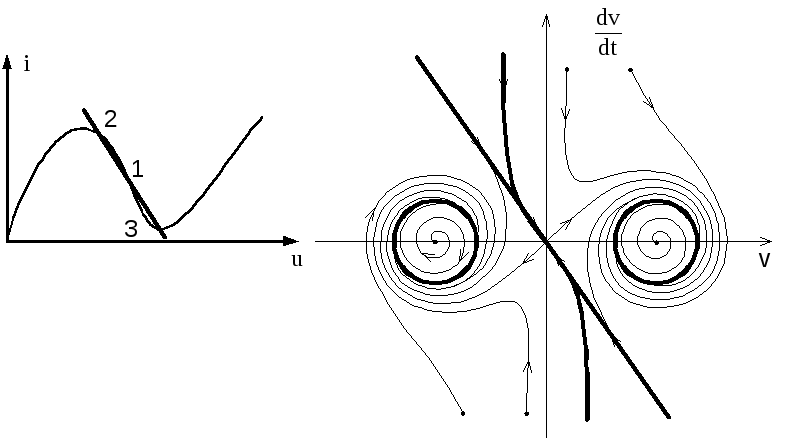
Рис.3.73. ВАХ и фазовые портрет схемы (рис.3.64) в случае, когда

все особые точки неустойчивые

току устойчива когда 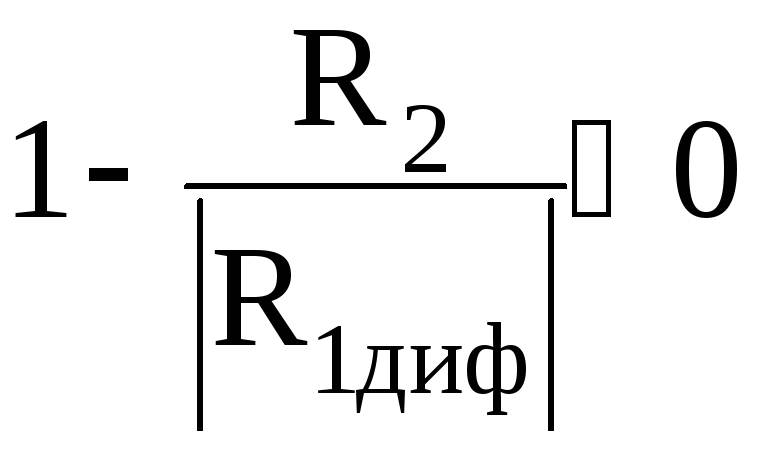. Замечая, что, обнаруживаем совпадение критериев устойчивости. Причем метод фазовой плоскости указывает, что произойдет в цепи при выполнении условия.

б) В методе линеаризации было получено условие устойчивости колебаний в окрестности устойчивой рабочей точки >. В методе фазовой плоскости, с учётом, условие устойчивости>совпадает с>.

в) Методом гармонической линеаризации были рассмотрены стационарные автоколебания (для случая ). На фазовой плоскости этим колебаниям соответствует предельный цикл.

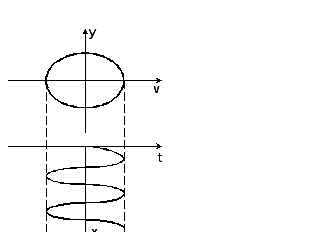
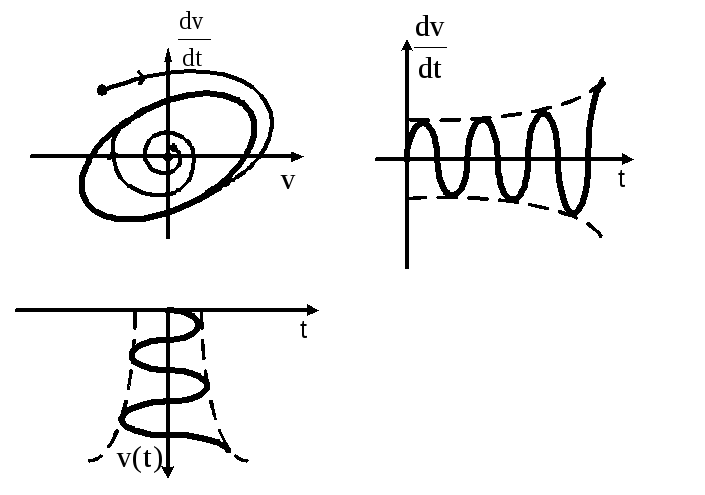
а) б)

Рис.3.74. а).Фазовый портрет автогенератора и б) предельный цикл

и амплитуда установившихся колебаний

г) Метод медленно меняющихся амплитуд позволил получить решение, включающее в себя результаты, как метода линеаризации, так и МГЛ.

Литература:

1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. – М.: Наука. Гл. ред. физ.-мат. лит., 1981. – 568 с.

2. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний: учебное руководство/ под ред. В.В. Мигулина. – 2-е изд., перераб. – М.: Наука. Гл. ред. Физ.-мат. Лит., 1988. – 392 с.

3. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. – М.: Наука, 1974. – 503 с.

4. Моисеев Н.Н. Асимтотические методы нелинейной механики. – 2-е изд., перераб. – М.: Высшая школа, 1985.- 453 с.

5. Капранов М.В., Кулешов В.Н., Уткин Г.Н. Теория колебаний в радиотехнике. Учебное пособие для вузов. – М.: Наука. Гл. ред. физ.-мат. лит., 1984. – 250 с.

6. Андреев В.С. Теория нелинейных электрических цепей. М.: Связь, 1972. – 328 с.

7. Деч Г. Руководство к практическому применению преобразования Лапласа и Z-преобразования. М.: Наука. Гл. ред. физ.-мат. лит., 1981. – 288 с.

8. Сиберт У.М. Цепи. Сигналы. Системы. В 2-х частях М.: Мир, 1988. – 336с и ……

9. Бессонов Л.А. Нелинейные электрические цепи. - 3-е. изд., перераб. и допол. Учебное пособие для втузов. М.: Высшая школа, 1977. – 343 с.

10. Бутенко Н.В., Неймак Ю.И., Фуфаев Н.А. Введение в теорию нелинейных колебаний. Учебное пособие. Для втузов. – 2-е изд., испр., - М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 384 с.

СОДЕРЖАНИЕ

Введение 3

ГЛАВА І Свободные и вынужденные колебания в линейных

инвариантных динамических системах 7