§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде

Среди нелинейных дифференциальных уравнений в теории колебаний особую роль играет уравнение Ван-дер-Поля

(3.87)

Параметр ε в уравнении Ван-дер-Поля может изменяться в широких пределах от 10^-3 до 10⁴. Уравнение Ван-дер-Поля (3.87) описывает процесс развития и установления колебаний, как в автогенераторах гармонических колебаний (ε - малая величина ~ 10^-2 ÷ 10^-3 ), так и в генераторах релаксационных колебаний (ε - большая величина ~ 10² ÷ 10⁴).

Рабочую точку на ВАХ туннельного диода для автогенераторов выбирают на середине отрицательного участка ВАХ туннельного диода. Т.к. R₂ = 0, то нагрузочная линия пройдет перпендикулярно к оси абсцисс.

Аппроксимируем ВАХ полиномом третьей степени (укороченным полиномом)

φ(V)= - k₁V + k₂ V³,

где k₁ = | G_д | - туннельного диода.

Методы применяются для анализа вынужденных колебаний и для анализа процессов установления автоколебаний.

Основная идея метода малого параметра заключается в следующем: пусть дифференциальное уравнение (или система уравнений), описывающее поведение колебаний в цепи, удается представить в таком виде, что в его правую часть входит малый параметр ε. Например,

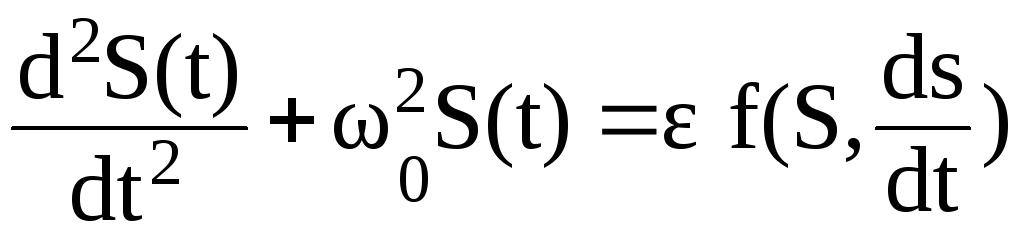. (3.88)

Если решение при известно и равноS₀(t), тогда при решениеS(t) ищется в виде ряда по степеням малого параметра

(3.89)

Максимальная величина степени ε в решении определяет степень приближения. Путем подстановки решения вида (3.89) в исходное уравнение (3.88) и выполнения ряда преобразований можно получить уравнение для определения поправок приближений S_ν(t). Обычно первое приближение находится легко, второе находится значительно труднее первого, третье еще труднее и т.д. Однако, часто удовлетворительным оказывается уже первое или второе приближение.

Быстро и правильно выбрать порождающее решение S₀(t) и определить, что следует использовать в качестве малого параметра ε, удается только для уравнений второго порядка.

Существуют различные разновидности методов малого параметра. Наиболее строгим является асимптотический метод Крылова-Боголюбова.

Рассмотрим подробно один из методов малого параметра – метод медленно меняющихся амплитуд, анализируя с его помощью установление колебаний в автогенераторе на туннельном диоде.

В методе медленно меняющихся амплитуд предполагается, что кроме условия малости параметра ε << 1, выполняется условие малости относительного изменения амплитуды S за период Т, т. е. .

Схема автогенератора на туннельном диоде представлена на рис 3.55,

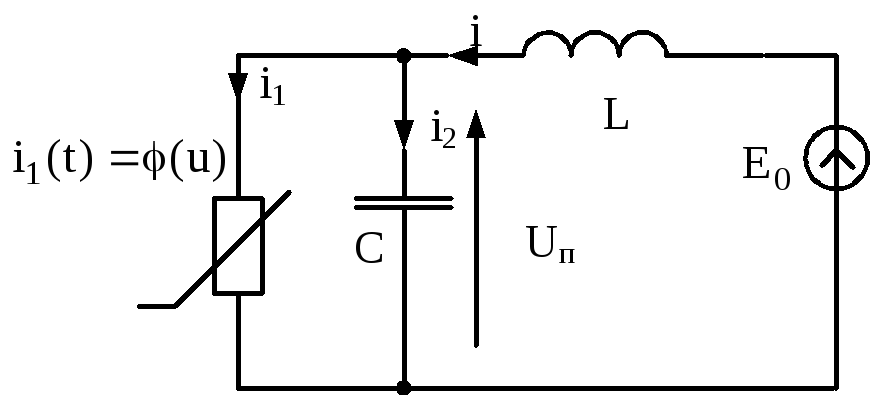
Рис.3.55. Схема автогенератора гармонических колебаний

Уравнение, описывающее колебание в цепи можно составить, используя первый и второй законы Кирхгофа (аналогично (3.27 – 3.28))

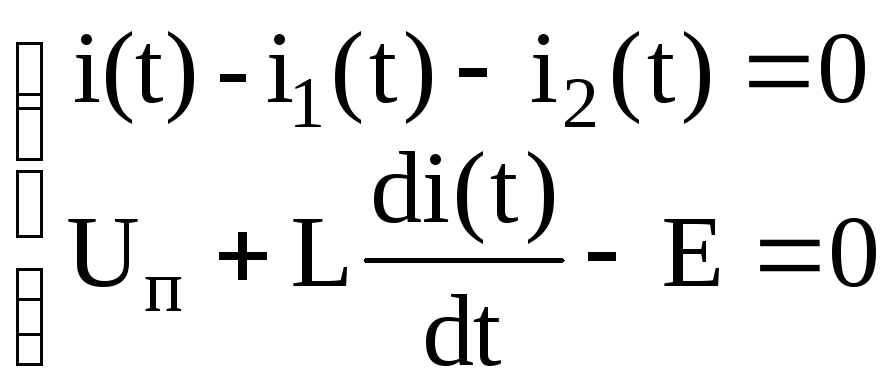. . (3.90)

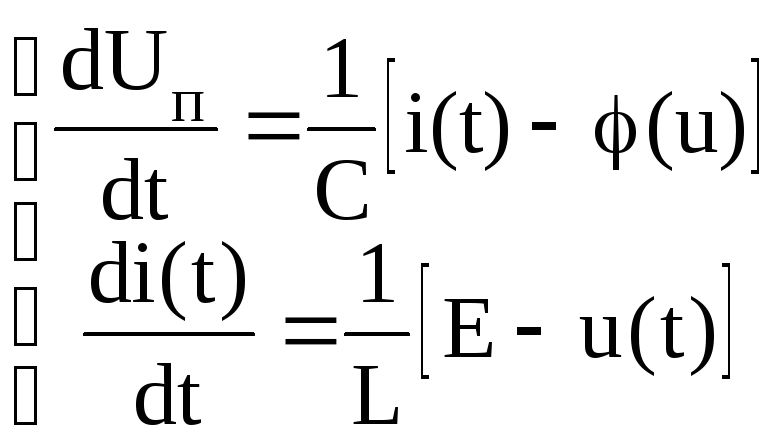. (3.91)

После дифференцирования получим

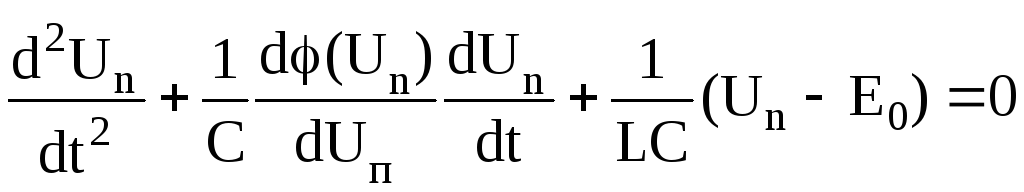. (3.92)

Полное напряжение U_n (U_n=E₀ + U) содержит постоянную составляющую Е₀ и переменную U.

Для переменной составляющей дифференциальное уравнение принимает вид

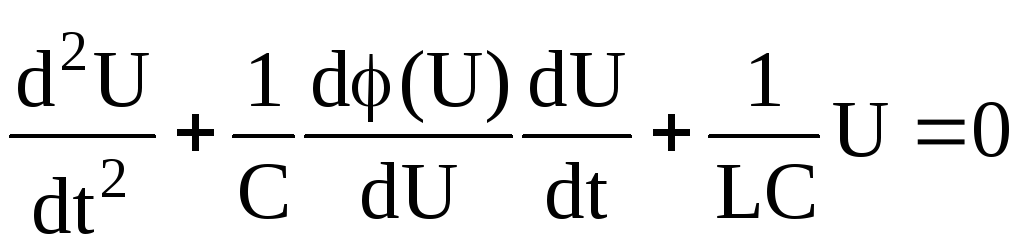. (3.92)

Используя для ВАХ туннельного диода аппроксимацию полиномом третей степени

, (3.94)

получим

. (3.95)

Введем безразмерное время , тогда , а уравнение (3.95) примет вид

. (3.96)

Введем новую переменную и обозначим. Тогда уравнение (3.96) примет вид:

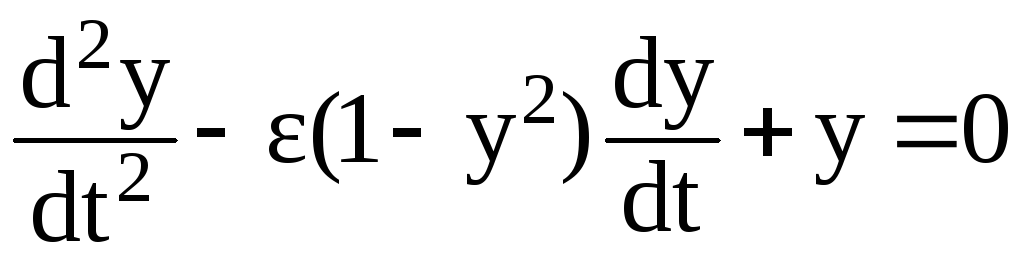(3.97)

− уравнение Ван-дер-Поля.

Уравнение Ван-дер-Поля описывает колебательные процессы в большом классе разнообразных нелинейных цепей. Параметр может принимать значение от долей единицы до сотен. Если<<1, то уравнение Ван-дер-Поля описывает колебательный процесс близкий к гармоническим колебаниям, если>>1 – то оно описывает релаксационный колебательный процесс.

Пусть в нашем случае , кроме того считаем, что .

В соответствии с уравнением (3.81) решение ищем в виде

(3.98)

Это связано с тем, что при , уравнение Ван-дер-Поля принимает вид

,

решением данного уравнения есть функции cosτ или sinτ. Поэтому при малых решение должно незначительно отличаться от:

.

Найдем производные и подставим результат в уравнение Ван-дер-Поля (3.97).

.

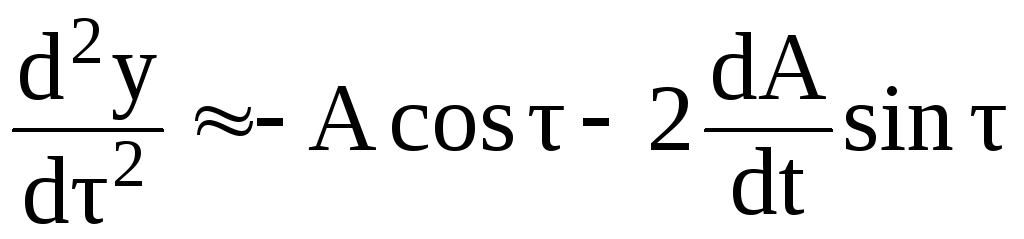
В последнем выражении, т.к. исследуемая схема (3.55) содержет резонансный контур, настроенный на основную частоту , слагаемыми с частотой 3ω, пренебрегаем. Подставляя найденные соотношения в уравнение Ван-дер-Поля получаем:

Выделяя слагаемые первого порядка малости (подчеркнутые), получим следующее уравнение:

Здесь приравняли нулю коэффициент при sinτ, т.к. sinτ=0 только в отдельных точках. Если разделить уравнение на А, получим:

. (3.99)

Для установившихся, т.е для стационарных колебаний . Следовательно, из формулы (3.99) следует, что

4А²_ст=А⁴_ст,

откуда А_ст=2 или А_ст=0.

Второе значение, стационарной амплитуды не интересно, т.к. он показывает, что колебания вообще не возникли.

Таким образом . Учитывая введенные обозначения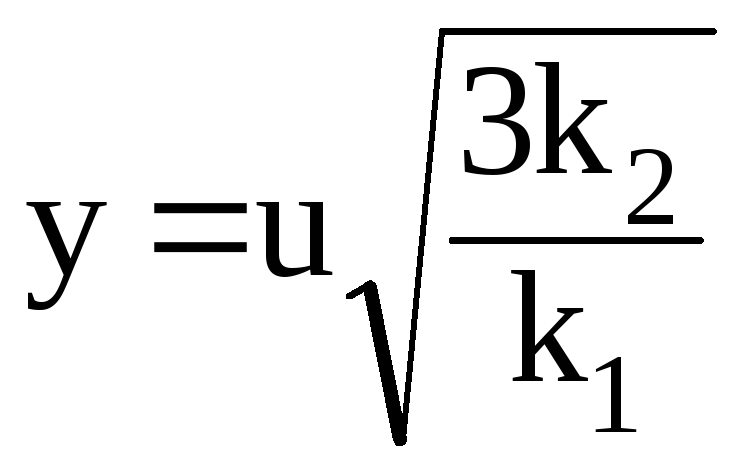, получаем что

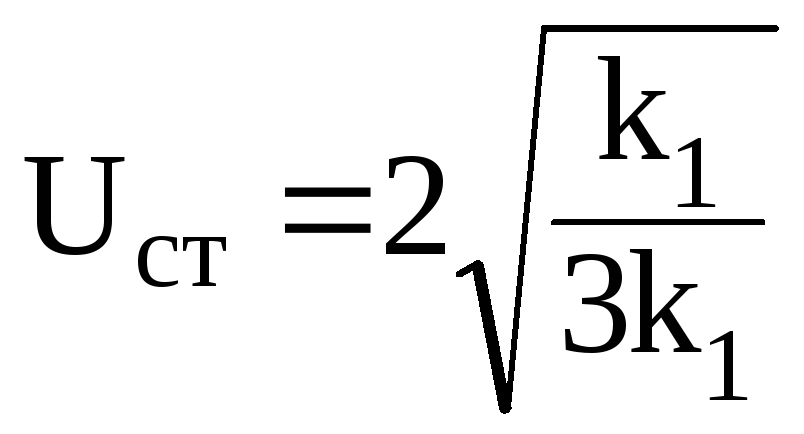. (3.100)

Этот результат был получен при использовании метода гармонической линеаризации.

Возвращаясь к уравнению (3.99), описывающему амплитуды колебаний в автогенераторе и вводя следующую замену переменных

, (3.101)

получаем новое уравнение

,

откуда

. (3.102)

Разделяем переменные и интегрируем

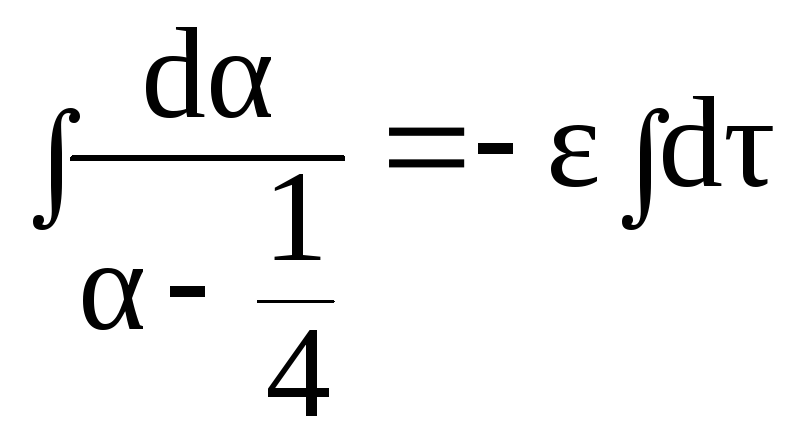, (3.103)

,

,

,

Тогда из равенства (3.101) следует

. (3.104)

Возвращаясь к переменным y(τ) и U(τ), находим

,

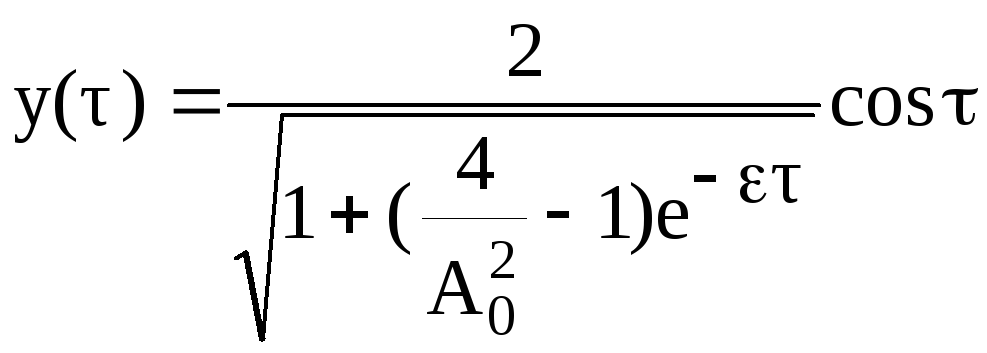. (3.105)

Из формулы (3.104) следует, что:

1) по мере увеличения безразмерного времени ,или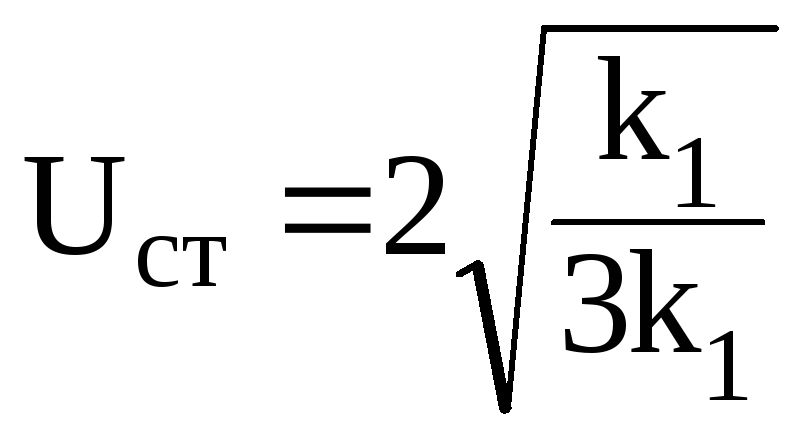(этот результат был найден ранее с помощью метода гармонической линеаризации и является признаком правильности полученного результата)

2) при малых , а также при малой начальной амплитуде колебаний А₀<<1, имеем

,

поэтому

.

Тогда, с учетом введенных обозначений,

,

начальная стадия развития колебаний автогенератора развивается в соотвествии с формулой:

.

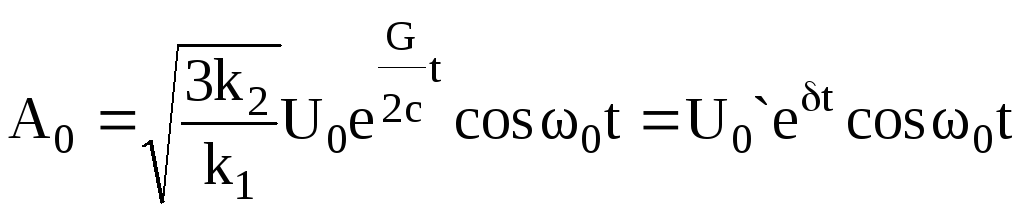Получен знакомый по методу линеаризации результат – экспоненциальное нарастание амплитуды пока колебания малы. Т.е. метод медленно меняющихся амплитуд объединил результаты методов линеаризации и метода гармонической линеаризации и позволил, кроме того, определить характер установления колебаний.