§3.8. Методы малого параметра. Метод последовательных приближений

Уже в прошлом столетии существовал математический аппарат, который при надлежащем развитии и обобщении мог бы быть применим для исследования нелинейных колебаний, во всяком случае, для колебаний, достаточно близких к линейным. Достаточно близкими к линейным обычно называются колебания, для которых соответствующее дифференциальное уравнение хотя и является нелинейным, но содержит некоторый параметр ε, входящий в это уравнение так, что при равенстве нулю этого параметра, нелинейное дифференциальное уравнение вырождается в линейное с постоянными коэффициентами. При этом предполагается, что параметр ε является «малым». Говоря о таком математическом аппарате, имелось в виду, прежде всего теория возмущений, разработанная для изучения движения планет.

Идея метода последовательных приближений заключается в представлении решения нелинейного уравнения, содержащего малый параметр ε, в виде степенного ряда по малому параметру ε.

x(t) = x₀ + εx₁ + ε²x₂ + ε³x₃ + …

Существенная трудность метода, состоит в невозможности использования полученных решений за достаточно длительный промежуток времени. Дело в том, что обычные разложения по степеням малого параметра приводят для искомых величин, характеризующих движение, к приближенным формулам, в которых наряду с членами, гармонически зависящих от времени, присутствуют еще и так называемые секулярные слагаемые вида

t^msinω t, t^mcosω t ,

в которых время t входит вне sin или cos. Вследствие этого область применимости получаемых приближенных формул ограничена слишком коротким интервалом времени.

Рассмотрим конкретное уравнение

; где α > 0 и γ > 0, (3.69)

которое может интерпретироваться как уравнение незатухающих колебаний некоторой массы m, притягиваемой к положению равновесия восстанавливающей упругой силой

p(x) = α x + γ x³. (3.70)

Будем считать, что . Причем ε мало. Образуем приближенное решение с точностью до величин второго порядка малости

х(t) = x₀(t) + εx₁(t). (3.71)

Подставляя приближение (3.71) в уравнение (3.69) и, группируя слагаемые по степеням малого параметра ε, находим

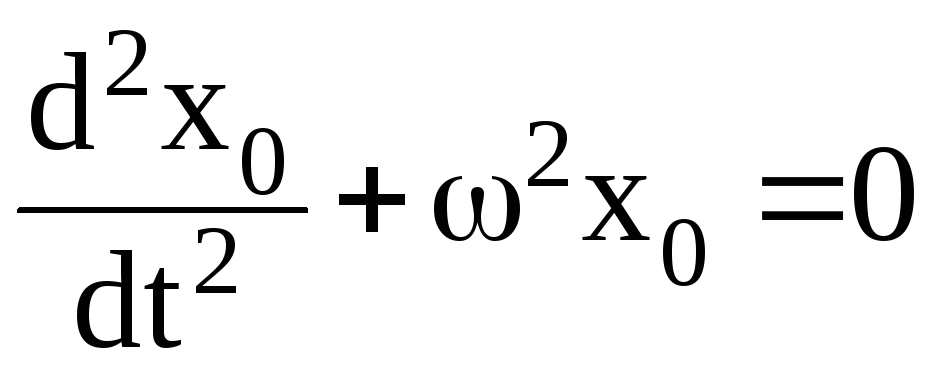; (3.72)

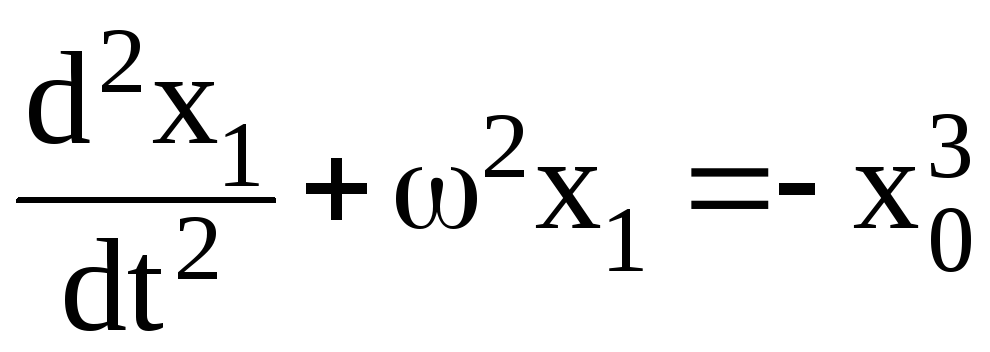; (3.73)

Из уравнения (3.72) находим

х₀ = аcos(ω t + θ) (3.74)

и, подставляя в правую часть уравнения (3.73), получаем

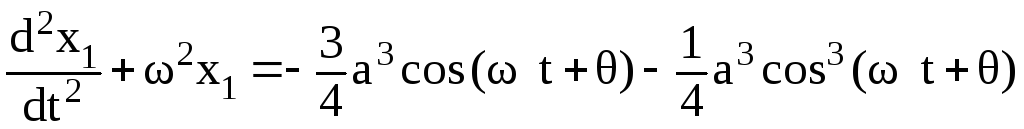. (3.75)

Из математического анализа известно, что если правая часть линейного дифференциального уравнения с постоянными коэффициентами имеет вид е^px(A₀x^s + A₁x^s-1 + … + A_s), то, если р не является корнем характеристического уравнения, частное решение нужно искать в виде

Если же р является корнем характеристического уравнения кратности α (этот случай называется особым или резонансным), то частное решение надо искать в виде

Так как в нашем случае для уравнения (3.75) мы имеем резонансное решение, то после отыскания коэффициентов находим

x(t) = acos(ω t + θ) (3.76)

В найденном решении имеется секулярное слагаемое

и, следовательно, колебания представленные формулой (3.76) должны раскачиваться, а их амплитуда при неограниченном возрастании t должна неограниченно возрастать, что находится в явном противоречии с характером точного решения уравнения (3.69), которое выражается через элиптические функции и имеет следующий вид:

x(t) = x_max cn,

где cn и K обозначают соответственно элиптический косинус и полный элиптический интеграл первого рода.

Ряд (3.76) из-за присутствия секулярных членов не пригоден не только для количественного, но и для качественного анализа поведения решения уравнения (3.69) на всей действительной оси. Заметим еще раз, что наличие в разложении (3.76) секулярных членов ни в коем случае не означает, что уравнение (3.69) вообще не имеет периодических решений. Это свидетельствует только о несоответствующем выборе разложения.