
- •Министерство образования и науки украины
- •Введение
- •Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах
- •§1.1.Преобразование Лапласа и его основные свойства
- •§ 1.2. Применение операторного метода для анализа процессов в цепях с сосредоточенными элементами
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях
- •§1.4 Общий вид решения задачи анализа прохождения сигнала через устойчивую линейную цепь
- •Алгоритм решения задач анализа вынужденных колебаний в электрических цепях
- •§1.5. Свободные колебания в динамических системах с распределенными элементами
- •§1.5.1. Классификация длинных линий
- •§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •Глава іі Колебания в линейных параметрических системах Линейные параметрические цепи
- •§ 2.1. Изменение спектра входного сигнала при прохождении через линейные параметрические цепи
- •§ 2.2. Аксиоматика теории цепей в параметрическом случае
- •§2.3. Прохождение сигналов через параметрические r – цепи
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с одной степенью свободы. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.5.1. Процессы в механической параметрической колебательной
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье
- •§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
- •§2.8. Параметрический генератор (параметрон)
- •§2.9. Двухконтурные параметрические системы
- •§2.9.1.Теорема Менли-Роу
- •§2.9.2 .Двухконтурный параметрический усилитель нерегененративного типа
- •§2.9.3 .Двухконтурный параметрический усилитель регененративного типа
- •§ 2.9.4 Параметрические умножение и деление частоты
- •§2.11. Некоторые приближенные методы исследования процессов в параметрических системах
- •§2.11.1. Метод «замороженного» параметра
- •§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях
- •§2.11.3 Метод последовательных приближений
- •§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)
- •Глава ш Анализ колебаний в нелинейных цепях
- •§3.1. Нелинейные элементы цепей
- •§3.2 Аппроксимация характеристик нелинейных элементов
- •§3.3 Преобразование спектра колебаний нелинейной цепью
- •§3.4 Особенности задач анализа колебаний в нелинейных цепях
- •§3.5 Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений
- •§3.6. Метод линеаризации
- •§3.7. Метод гармонической линеаризации (мгл)
- •§3.7.1. Эквивалентные параметры нелинейных элементов
- •§3.7.2. Автогенератор гармонических колебаний.
- •§3.8. Методы малого параметра. Метод последовательных приближений
- •§3.9. Метод медленно меняющихся амплитуд (ммма).
- •§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде
- •§3.11. Метод фазовой плоскости
- •§3.11. 1.Метод фазовой плоскости. Метод изоклин
- •§3.11.2. Метод фазовой плоскости. Особые точки
- •§3.11.2.Исследование методом фазовой плоскости схемы на
- •§1.1. Преобразование Лапласа и его основные свойства 7
- •610077,М. Харків, пл. Свободи, 4.
- •610077,М. Харків, пл. Свободи, 4.
§2.11.3 Метод последовательных приближений
Пусть у нас имеется линейная параметрическая цепь рис.2.38. В такой цепи могут существовать как свободные, так и вынужденные колебания.

Рис.2.38. Линейная параметрическая цепь
Пусть колебания параметров происходят значительно медленнее по сравнению с характерными колебаниями напряжения или тока в линейной параметрической цепи. Это условие, также как и для метода «замороженного» параметра, является основным условием накладывающим ограничение для применимости метода последовательных приближений. Метод последовательных приближений позволяет получить ряд последовательных поправок к методу «замороженного» параметра.
Пусть у нас имеется система с сосредоточенными параметрами (радиотехническая цепь). Система интегродифференциальных уравнений описываюшяя колебания в такой цепи, содержит коэффициенты, зависящие от параметра – времени
![]() .
(2.109)
.
(2.109)
Считаем,
что можно представить матрицу
![]() в виде постоянной величины и, медленно
изменяющейся вокруг нее, переменной
части:
в виде постоянной величины и, медленно
изменяющейся вокруг нее, переменной
части:
![]() .
(2.110)
.
(2.110)
Тогда подставим равенство (2.110) в уравнение (2.109) и перепишем его в следующем виде:
![]() .
(2.111)
.
(2.111)
Будем искать решение в виде знакопеременной суммы матриц-столбцов неизвестных функций:
![]()
![]() (2.112)
(2.112)
Подставим ряд (2.112) в уравнение (2.111) и запишем его в следующем виде:
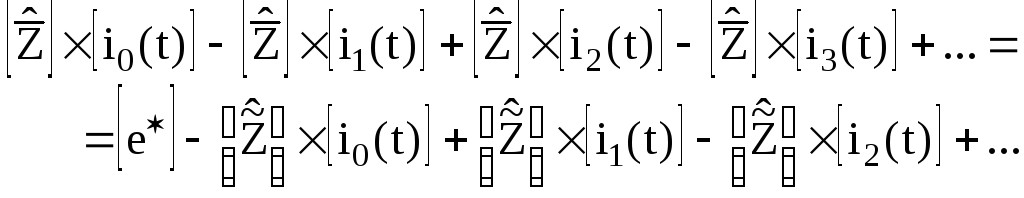 .
(2.113)
.
(2.113)
Обычно,
ряд (2.112) ограничевают каким-то конечным
числом слагаемых. Вид ряда (2.112) говорит
о том, что мы ищем решение в виде
последоватльного приближения к точному
решению. Будем считать, что мы хотим
построить решение с помощью метода
последовательных приближений до n-го
порядка точности. Тогда нам необходимо
найти n
неизвестных матриц-столбцов токов
![]() .
Но уравнение (2.111) у нас одно, поэтому
для получения однозначного решения для
тока
.
Но уравнение (2.111) у нас одно, поэтому
для получения однозначного решения для
тока![]() из уравнения (2.111), выберем удобные для
нас (n-1)
условий, выполнение которых поможет
получить (n-1)
–
дополнительных уравнений. Последнее
уравнение получим используя выражение
(2.113), в которое подставим наши условия.
Для получения первого уравнения,
потребуем, чтобы матрица-столбец
неизвестных токов
из уравнения (2.111), выберем удобные для
нас (n-1)
условий, выполнение которых поможет
получить (n-1)
–
дополнительных уравнений. Последнее
уравнение получим используя выражение
(2.113), в которое подставим наши условия.
Для получения первого уравнения,
потребуем, чтобы матрица-столбец
неизвестных токов
![]() находилась как решение следующего
уравнения:
находилась как решение следующего
уравнения:
![]() .
(2.114)
.
(2.114)
Второе
уравнение получим, потребовав, чтобы
матрица-столбец неизвестных токов ![]() находилась как решение уравнения:
находилась как решение уравнения:
![]() (2.115)
(2.115)
и т.д. Мы получили ряд уравнений для нахождения (n-1) поправки для решения в виде выражения (2.112).
![]() ,
(2.116)
,
(2.116)
. . . . . . . . . . . . . . . . . . . . . . . . . . .
![]() .
.
Последнее же уравнение получим, подставив найденные уравнения в формулу (2.113), из которого следует, что для нахождения последней поправки, необходимо решить следуюшее уравнение:
![]() .
(2.116)
.
(2.116)
Теперь
у нас n
уравнений для n
неизвестных. Находя из уравнения (2.114)
неизвестную матрицу-столбец токов ![]() ,
подставляем ее в правую часть уравнения
(2.115). Тогда в уравнении (2.115) справа будет
стоять известная функция и мы можем
найти первую поправку к решению
,
подставляем ее в правую часть уравнения
(2.115). Тогда в уравнении (2.115) справа будет
стоять известная функция и мы можем
найти первую поправку к решению ![]() .
Применяя эту процедуру к последующим
уравнениям, мы сможем последовательно
найти и остальные приближения. Причем,
если сравнить уравнение (2.114) с уравнением
(2.96) из метода «замороженного» параметра,
можно сделать вывод, что нулевое
проближение метода последовательных
приближений совпадает с решением метода
«замороженного» параметра. Для решения
уравнений (2.114-2.116) теперь можно применить
операторный метод, т.к. коэффициенты
матрицы
.
Применяя эту процедуру к последующим
уравнениям, мы сможем последовательно
найти и остальные приближения. Причем,
если сравнить уравнение (2.114) с уравнением
(2.96) из метода «замороженного» параметра,
можно сделать вывод, что нулевое
проближение метода последовательных
приближений совпадает с решением метода
«замороженного» параметра. Для решения
уравнений (2.114-2.116) теперь можно применить
операторный метод, т.к. коэффициенты
матрицы
![]() являются постоянными величинами.
являются постоянными величинами.
Применим преоразование Лапласа к уравнению (2.114) и получим систему алгебраических уравнений в операторном виде:
![]()
решение которой находится по правилу Крамера:
![]() .
.
После
нахождения решения для операторного
тока
![]() ,
осуществим обратное преобразование
Лапласа и найдем:
,
осуществим обратное преобразование
Лапласа и найдем:
![]() .
(2.117)
.
(2.117)
Полученное
выражение для столбцов контурных токов
в нулевом приближении, подставим в
уравнение (2.115) и получим известный
столбец функций в правой части уравнения
(2.115). С учетом полученной поправки найдем
первое приближение столбца контурных
токов
![]() ,
как решение уравнения (2.113).
,
как решение уравнения (2.113).
![]()
Последовательно осуществляя действия для остальных приближений, получим
![]() .
(2.118)
.
(2.118)
С помощью метода последовательных приближений можно найти решение для любого порядка точности. После этого, осушествляя обратное преобразование Лапласа к полученным решениям (2.118) окончательно найдем найдем решение параметрического уравнения:
![]() .
(2.119)
.
(2.119)
